一句话总结:Transformer 天生不知道文字的顺序,Positional Encoding 就是给每个位置加上独特的"门牌号",让模型能够区分"我爱你"和"你爱我"。
5.1 为什么需要位置信息?
上一章我们把文字转换成了向量。但这里有一个严重的问题:相同的字,不管在什么位置,Embedding 向量都是一样的。
5.1.1 一个关键问题
考虑这两个句子:
- "我爱你"
- "你爱我"
如果只看 Embedding,"我"在两个句子中的向量完全相同,"爱"完全相同,"你"也完全相同。
但这两个句子的意思完全不同!
问题出在哪里?缺少位置信息。
5.1.2 位置信息的三个作用

Positional Encoding 解决了三个问题:
-
每个 Token 都能包含它的位置信息
- 模型知道这是第 1 个字、第 2 个字、还是第 100 个字
-
模型可以看到文字之间的"距离"
- "我"和"爱"相邻,"我"和"你"隔了一个字
- 这种相对位置关系对理解语义很重要
-
模型可以学习到位置编码的规则
- 通过训练,模型能理解位置编码的模式
- 从而泛化到更长的序列
5.2 最简单的方案:直接用整数
在讲 Transformer 的方案之前,让我们先看最直观的方法。
5.2.1 整数位置编码
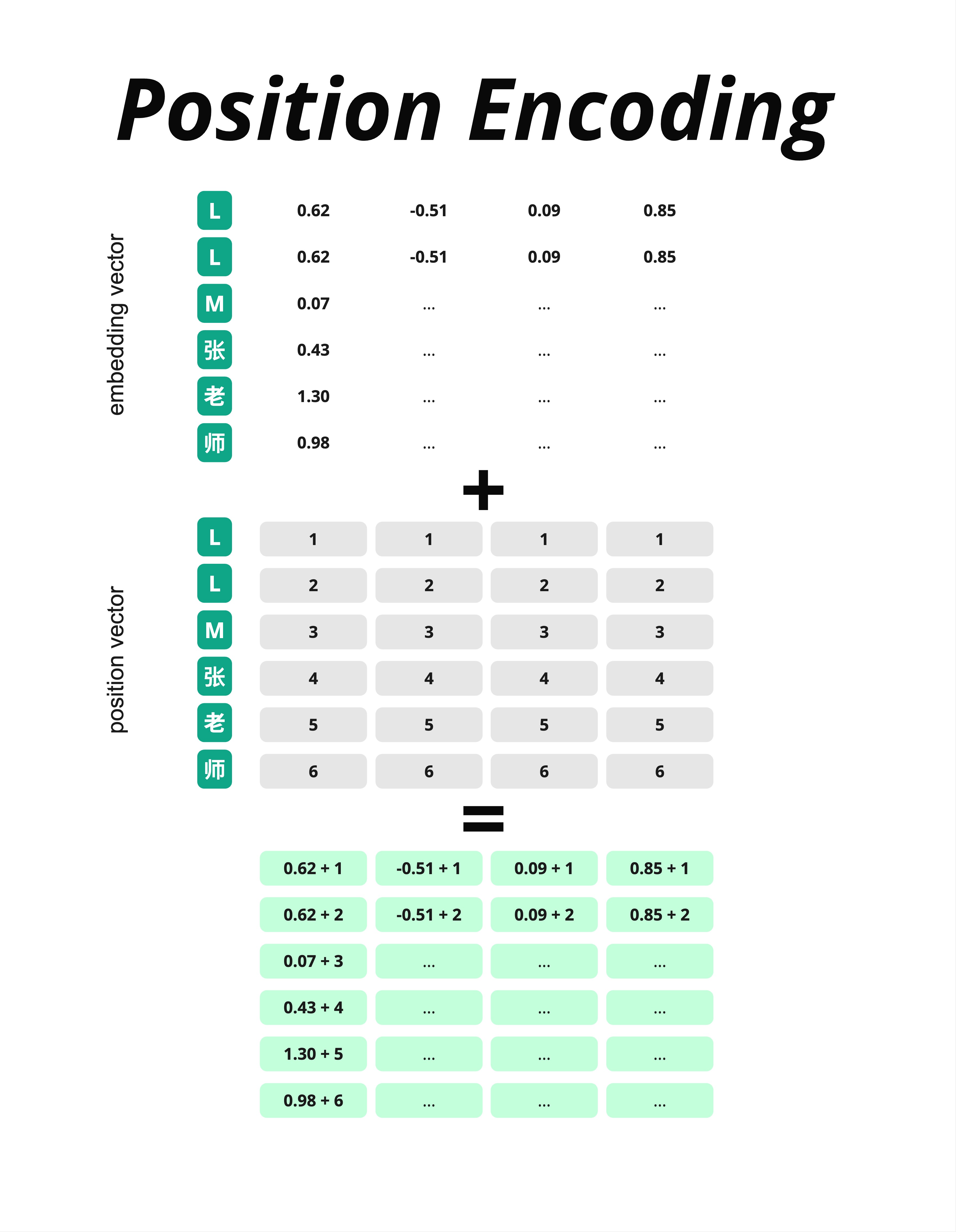
最简单的想法:直接把位置编号加到向量上。
假设输入是"LLM张老师":
Embedding 向量(每个字的语义表示):
| 字 | 维度1 | 维度2 | 维度3 | 维度4 |
|---|---|---|---|---|
| L | 0.62 | -0.51 | 0.09 | 0.85 |
| L | 0.62 | -0.51 | 0.09 | 0.85 |
| M | 0.07 | ... | ... | ... |
| 张 | 0.43 | ... | ... | ... |
| 老 | 1.30 | ... | ... | ... |
| 师 | 0.98 | ... | ... | ... |
位置向量(每个位置的编号):
| 位置 | 维度1 | 维度2 | 维度3 | 维度4 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 |
| 4 | 4 | 4 | 4 | 4 |
| 5 | 5 | 5 | 5 | 5 |
| 6 | 6 | 6 | 6 | 6 |
相加结果:
| 字 | 维度1 | 维度2 | 维度3 | 维度4 |
|---|---|---|---|---|
| L | 0.62+1 | -0.51+1 | 0.09+1 | 0.85+1 |
| L | 0.62+2 | -0.51+2 | 0.09+2 | 0.85+2 |
| ... | ... | ... | ... | ... |
5.2.2 整数方案的问题
这个方案简单直接,但有两个问题:
-
数值范围不可控:位置越靠后,加的数字越大。位置 1000 就要加 1000,这会让数值变得很大,影响训练稳定性。
-
没有规律可学:1, 2, 3, 4... 是线性增长的,模型很难从中学到有用的模式。
所以 Transformer 用了一个更聪明的方案:正弦位置编码(Sinusoidal Positional Encoding)。
5.3 Transformer 的方案:正弦位置编码
5.3.1 核心思想
Transformer 的位置编码使用 sin 和 cos 函数 来生成位置向量。
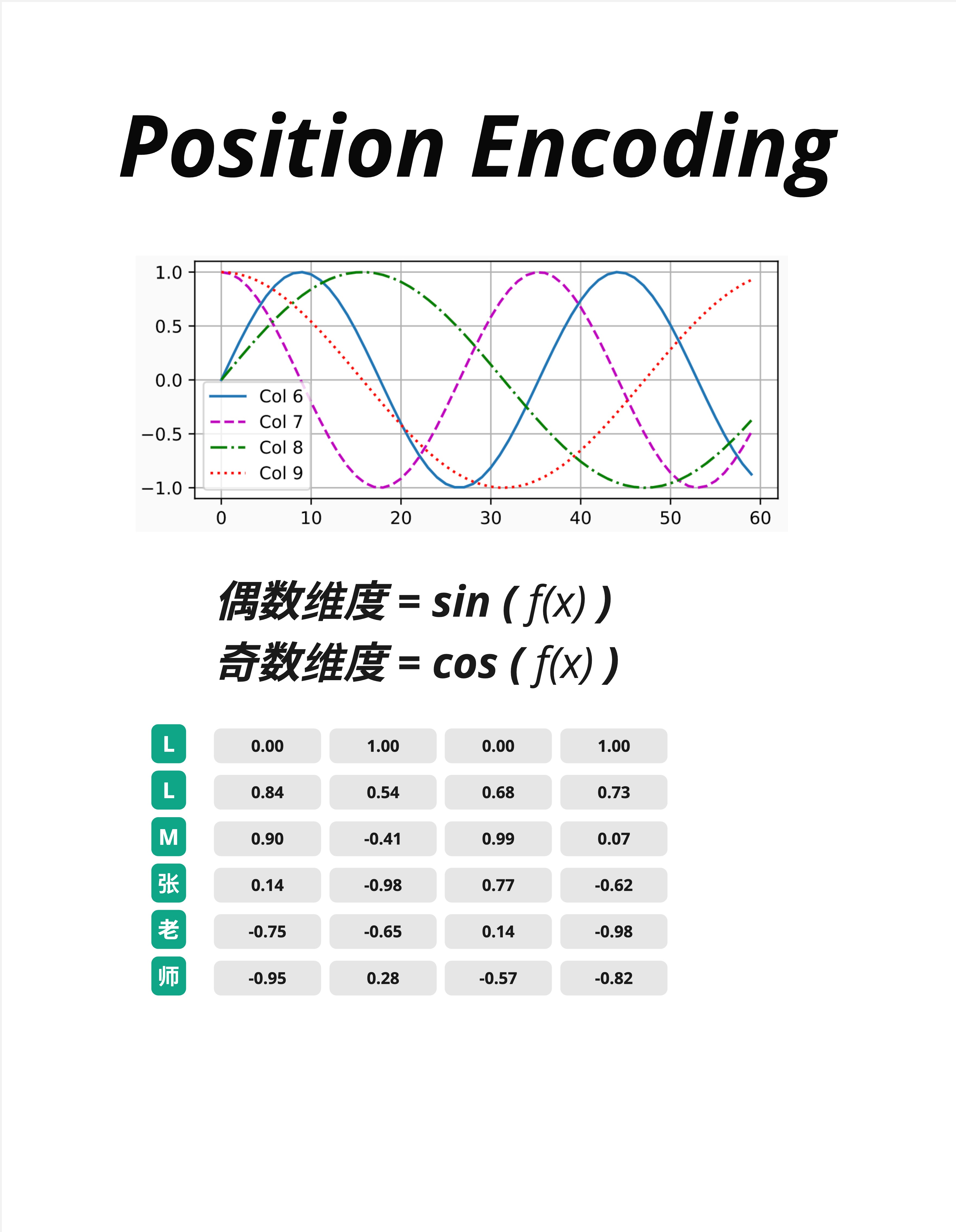
公式是:
偶数维度:PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
奇数维度:PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))别被公式吓到!核心思想很简单:
- 偶数维度用 sin 函数
- 奇数维度用 cos 函数
- 不同维度用不同频率的波
5.3.2 波形可视化
看图中的波形:
- Col 6(蓝色实线):频率最低,波长最长
- Col 7(紫色虚线):频率稍高
- Col 8(绿色点划线):频率更高
- Col 9(红色点线):频率最高,波长最短
每个维度都是一个不同频率的波。把所有维度组合起来,每个位置就有了独特的"指纹"。
5.3.3 实际数值
图中下方的表格展示了具体数值:
| 位置 | 维度0 | 维度1 | 维度2 | 维度3 |
|---|---|---|---|---|
| L (pos=0) | 0.00 | 1.00 | 0.00 | 1.00 |
| L (pos=1) | 0.84 | 0.54 | 0.68 | 0.73 |
| M (pos=2) | 0.90 | -0.41 | 0.99 | 0.07 |
| 张 (pos=3) | 0.14 | -0.98 | 0.77 | -0.62 |
| 老 (pos=4) | -0.75 | -0.65 | 0.14 | -0.98 |
| 师 (pos=5) | -0.95 | 0.28 | -0.57 | -0.82 |
注:位置从 0 开始编号(pos=0, 1, 2...)。pos=0 时 sin(0)=0, cos(0)=1。
注意:
- 所有数值都在 [-1, 1] 范围内(sin/cos 的值域)
- 每个位置的向量都是独特的
- 数值变化有规律可循
5.3.4 为什么用 sin/cos?
正弦位置编码有几个优点:
-
数值稳定:永远在 [-1, 1] 范围内,不会爆炸
-
可以外推:模型在短序列上训练,理论上能泛化到更长序列
-
相对位置可计算:sin/cos 有一个数学性质——两个位置的编码可以通过线性变换得到它们的相对位置
后来的研究发现,正弦编码的外推能力其实有限。更新的方案如 RoPE、ALiBi 效果更好,我们在第 25 章会详细介绍。
5.4 Embedding + Position = Input
现在让我们看完整的过程:把 Embedding 向量和位置向量加起来。
5.4.1 向量相加
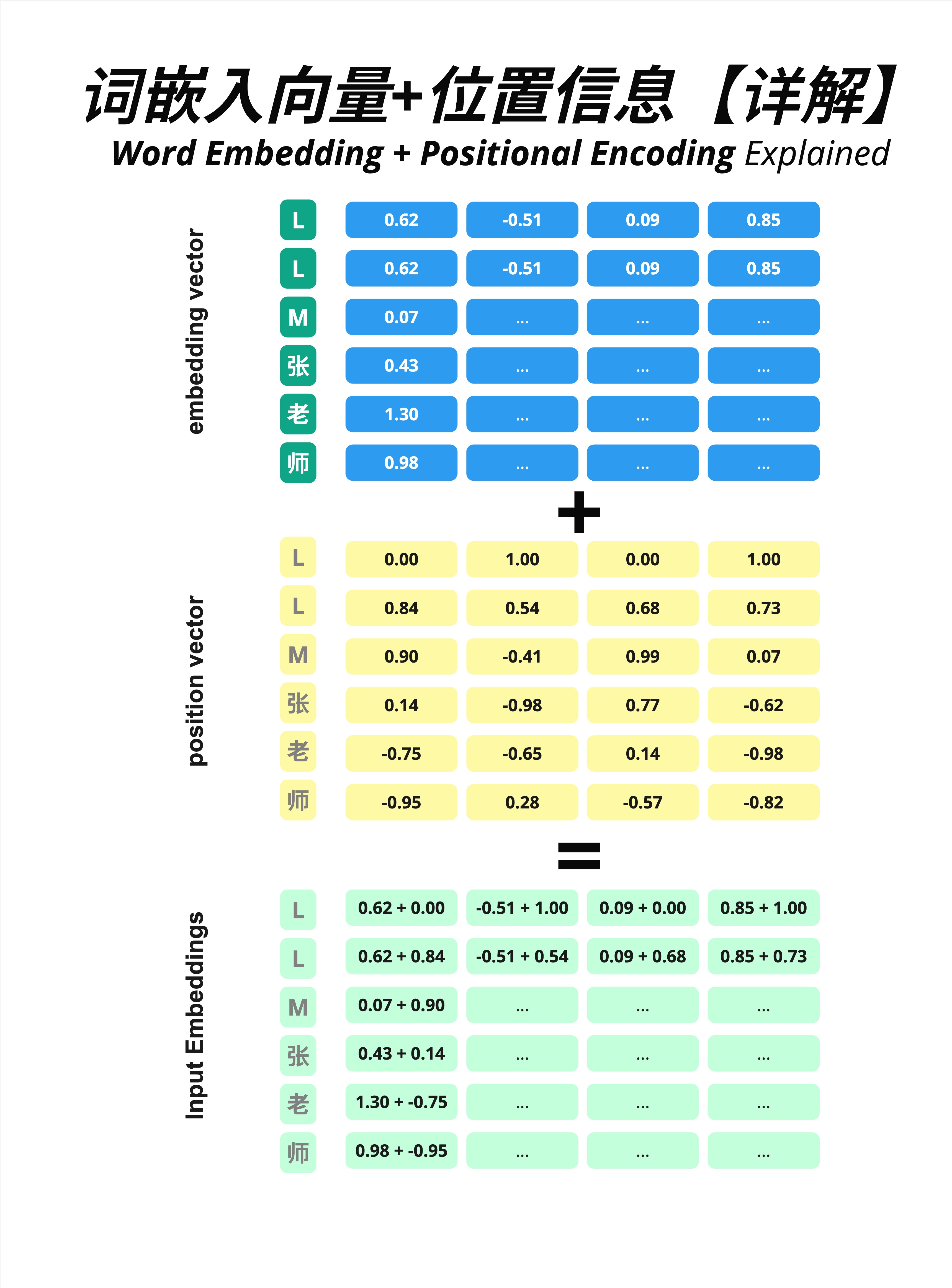
三个矩阵的关系:
Embedding Vector(蓝色):词的语义信息
L: [0.62, -0.51, 0.09, 0.85]
L: [0.62, -0.51, 0.09, 0.85] # 注意:两个 L 的 embedding 相同
M: [0.07, ..., ..., ...]
张: [0.43, ..., ..., ...]
老: [1.30, ..., ..., ...]
师: [0.98, ..., ..., ...]Position Vector(黄色):位置信息
位置1: [0.00, 1.00, 0.00, 1.00]
位置2: [0.84, 0.54, 0.68, 0.73]
位置3: [0.90, -0.41, 0.99, 0.07]
位置4: [0.14, -0.98, 0.77, -0.62]
位置5: [-0.75, -0.65, 0.14, -0.98]
位置6: [-0.95, 0.28, -0.57, -0.82]Input Embeddings(绿色):相加结果
L(位置1): [0.62+0.00, -0.51+1.00, 0.09+0.00, 0.85+1.00]
L(位置2): [0.62+0.84, -0.51+0.54, 0.09+0.68, 0.85+0.73]
...关键观察:两个 L 虽然 Embedding 相同,但加上不同的位置编码后,结果不同了!
这样模型就能区分"第一个 L"和"第二个 L"了。
5.4.2 几何直觉
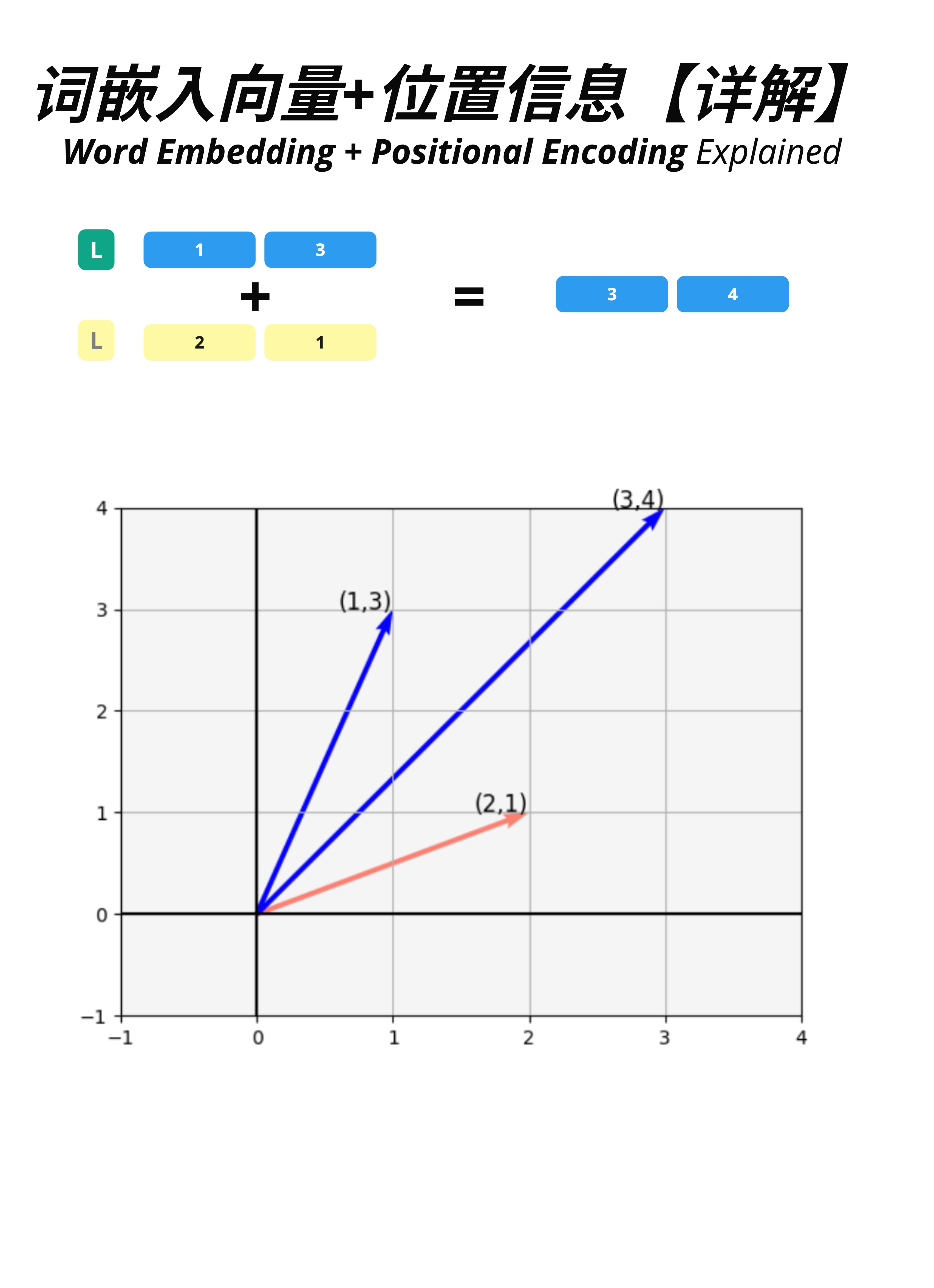
让我们用 2D 简化例子来理解向量相加的几何意义。
假设:
- Embedding 向量 L = [1, 3](蓝色箭头)
- Position 向量 = [2, 1](红色箭头)
相加结果:
- Input = [1+2, 3+1] = [3, 4](合成向量)
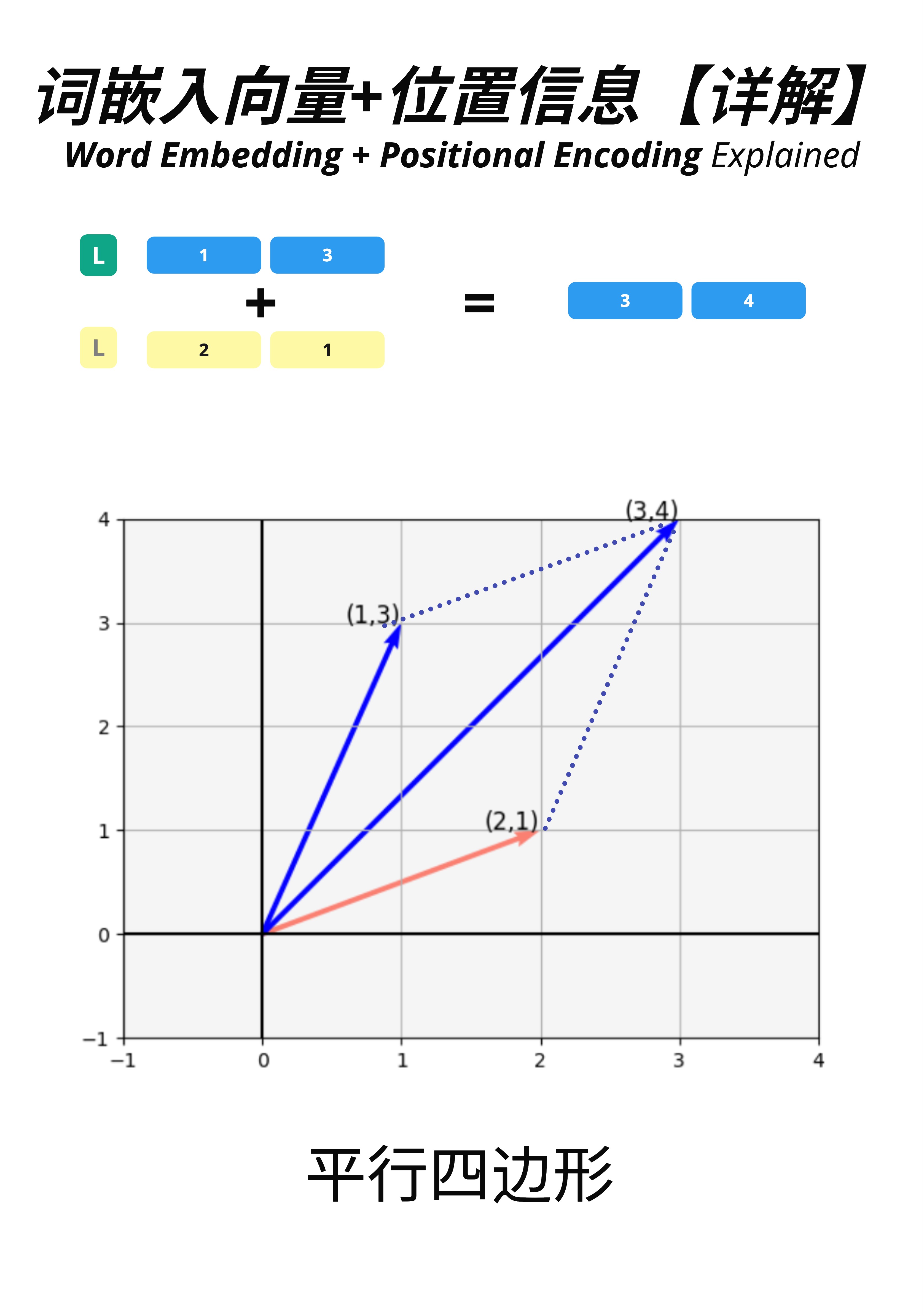
从几何上看,这就是向量加法的平行四边形法则:
- 两个向量首尾相接
- 结果是从原点到对角的向量
5.4.3 相对距离 vs 绝对位置
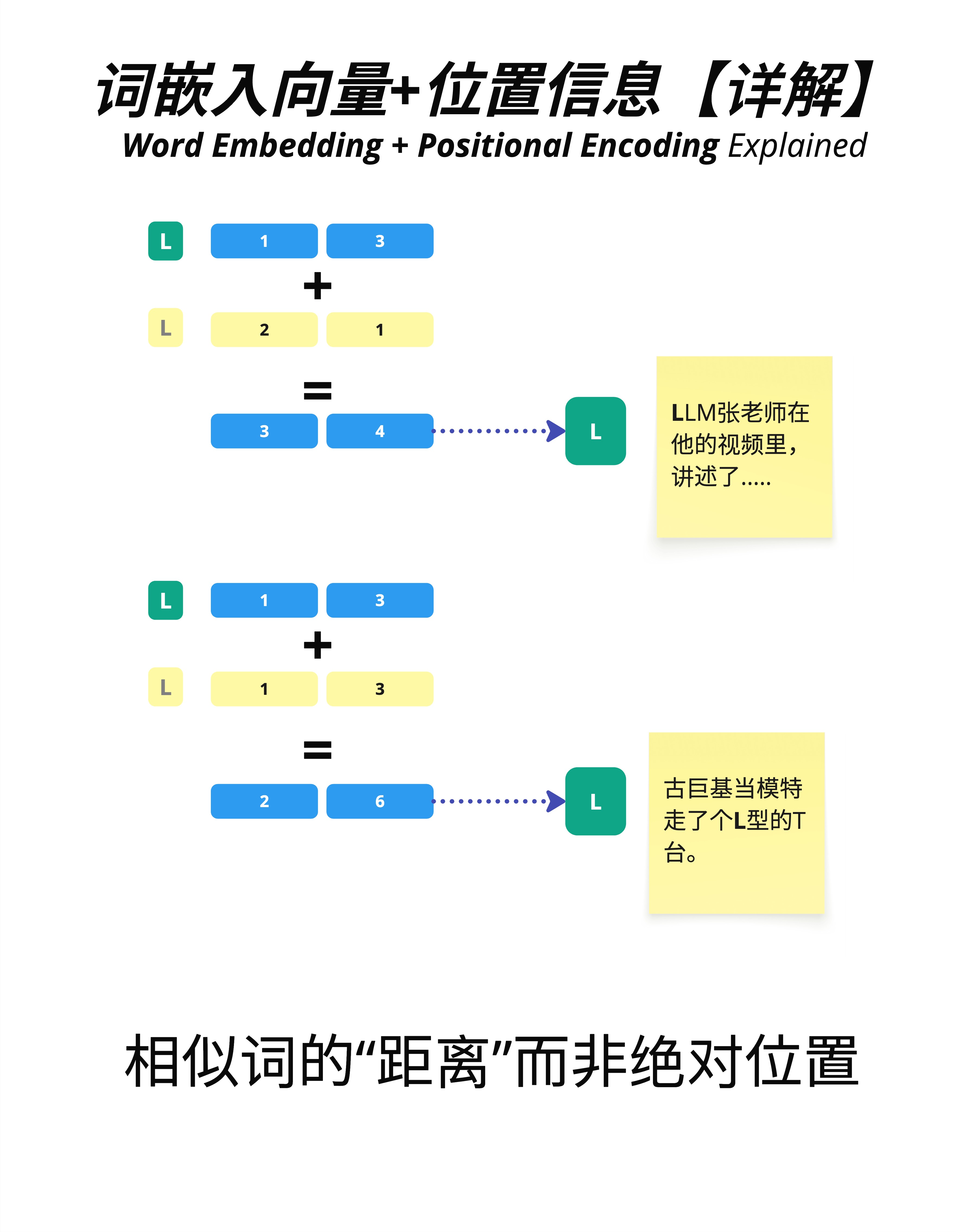
一个重要的洞察:在许多任务中,模型更关心的是"相对距离"而不是"绝对位置"。
注意:这并非绝对——不同的位置编码方案(如学习式 vs RoPE vs ALiBi)对绝对/相对位置的处理方式不同,详见第 25 章。
看图中的例子:
- 同一个字"L"出现在不同位置
- 位置 1 的 L:[1, 3] + [2, 1] = [3, 4]
- 位置 2 的 L:[1, 3] + [1, 3] = [2, 6](假设不同的位置编码)
虽然同一个词在不同位置的最终向量不同,但它们之间的"距离"是可以计算的。这让模型能够理解:
- "LLM张老师在他的视频里,讲述了..."——这里的"L"在句子开头
- "古巨基当模特走了个L型的T台"——这里的"L"在句子中间
同一个字,不同的位置,不同的上下文含义。
5.5 训练过程中的位置编码
5.5.1 Embedding 是可学习的,Position 是固定的
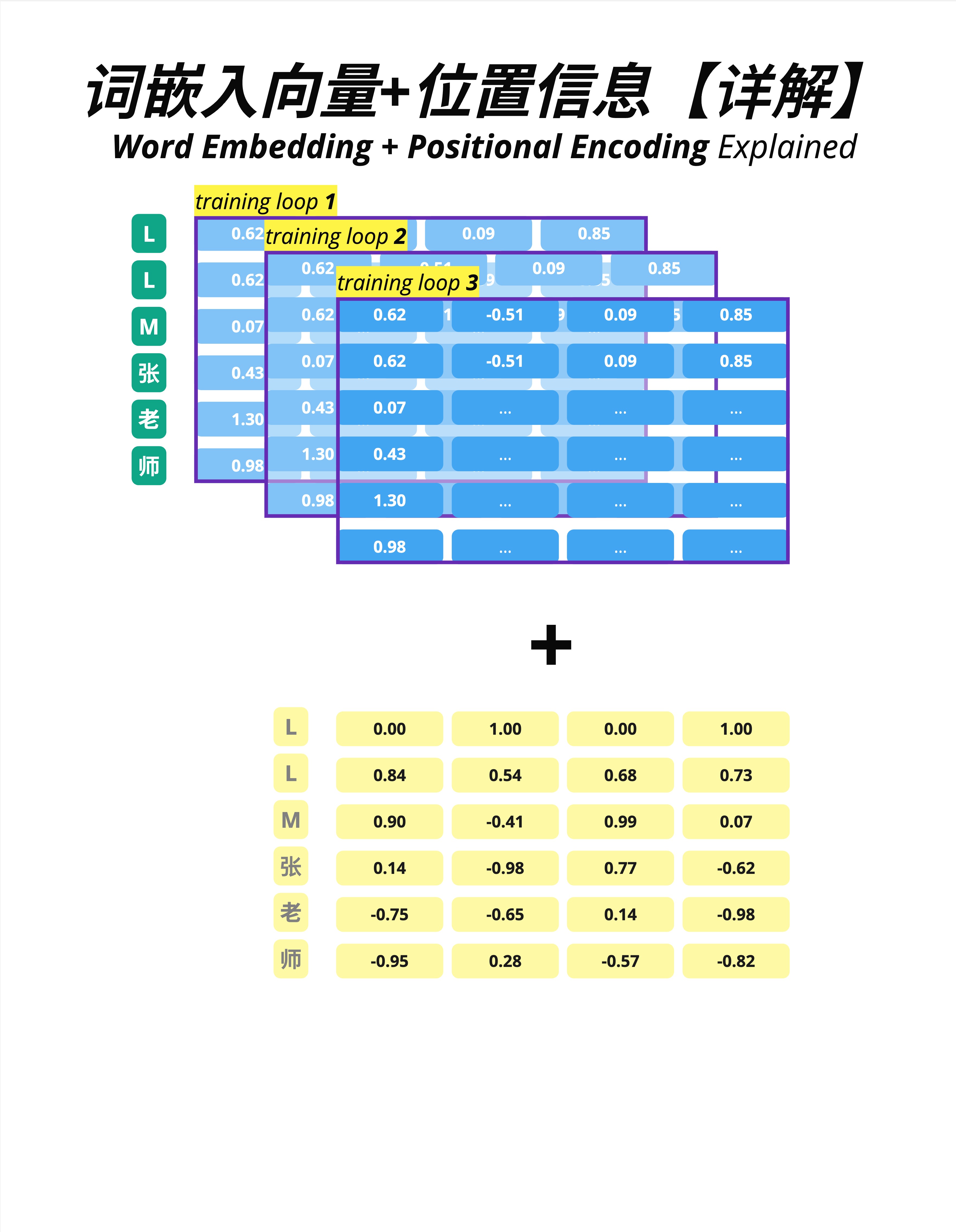
一个重要的区别:
- Embedding 向量:是模型参数,在训练过程中不断更新
- Position 向量(正弦版本):是固定的,不参与训练
图中展示了多轮训练(training loop 1, 2, 3...):
- Embedding 矩阵(蓝色)每轮都在变化
- Position 矩阵(黄色)始终不变
有些模型(如 BERT)使用"可学习的位置编码",Position 向量也作为参数训练。但原始 Transformer 使用的是固定的正弦编码。
5.5.2 在完整架构中的位置
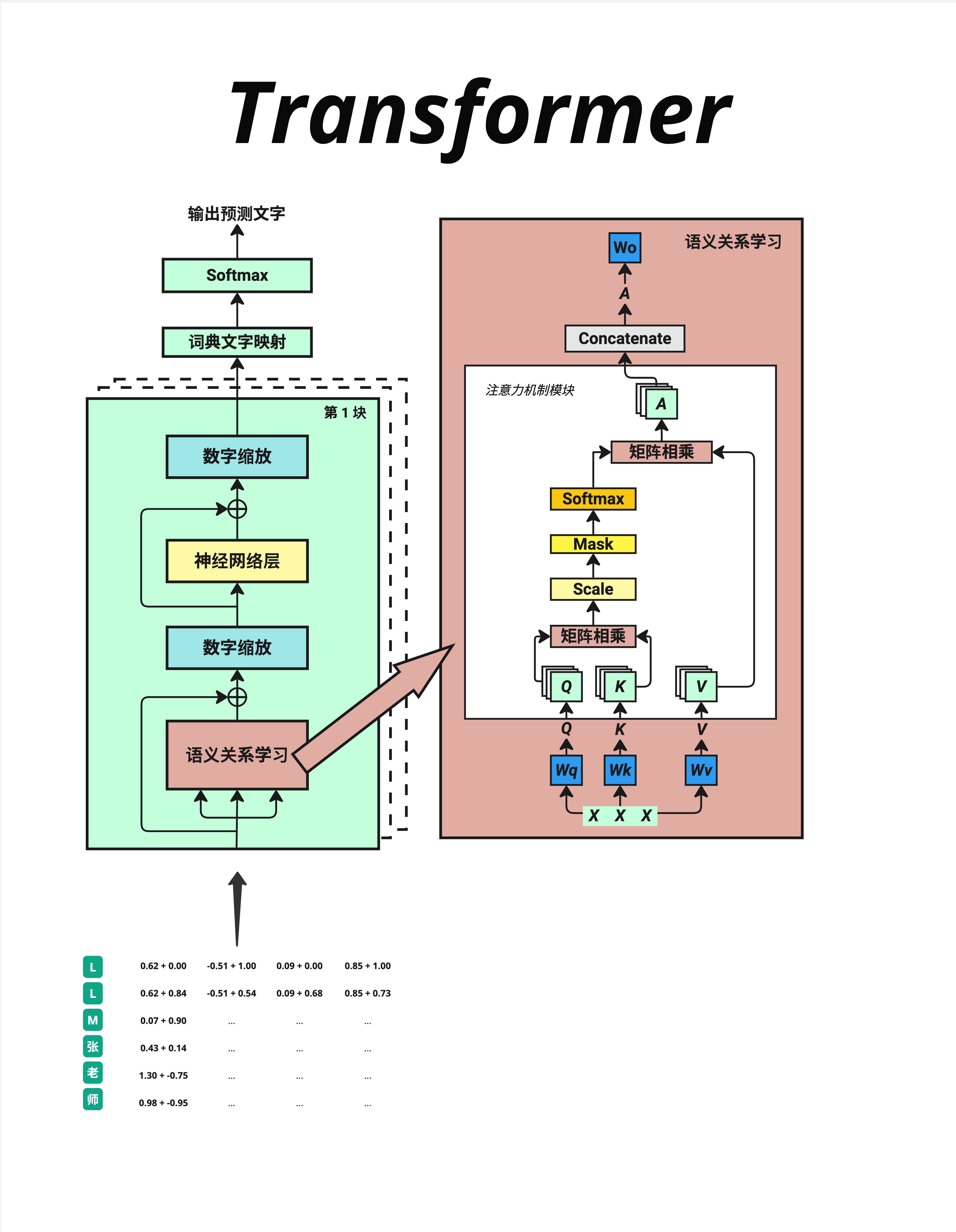
看这张详细的架构图:
- 输入文字经过 Embedding(文字转数字 → 嵌入向量)
- 加上 Positional Encoding(位置信息编码)
- 得到 Input Embeddings,送入 Attention 层
位置编码发生在进入 Transformer Block 之前,是预处理的一部分。
5.6 深入理解:为什么是"相加"?
你可能会问:为什么是把 Embedding 和 Position 相加?为什么不是拼接?
5.6.1 拼接 vs 相加
拼接(Concatenation):
- 把两个向量接在一起
- [embedding] + [position] → 更长的向量
- 优点:信息完全独立
- 缺点:维度翻倍,计算量增加
相加(Addition):
- 对应维度直接相加
- embedding + position → 相同维度的向量
- 优点:维度不变,计算高效
- 缺点:两种信息混合在一起
5.6.2 为什么相加可行?
关键洞察:高维空间很"宽敞"。
在 768 维或 4096 维的空间里,Embedding 信息和 Position 信息可以占据不同的"子空间"。相加后虽然混合了,但神经网络有足够的能力把它们分开。
这就像在一个巨大的房间里,放两套家具。虽然在同一个房间,但各自有各自的区域,不会混乱。
5.7 本章总结
这一章我们学习了 Transformer 如何处理位置信息。
5.7.1 核心概念
| 概念 | 解释 |
|---|---|
| Positional Encoding | 给每个位置添加独特的向量表示 |
| 正弦位置编码 | 用 sin/cos 函数生成位置向量 |
| 相加操作 | Embedding + Position = Input Embeddings |
| 相对位置 | 模型关心词之间的距离,而不只是绝对位置 |
5.7.2 数据变换过程
Embedding [seq_len, d_model] # 词的语义信息
+
Position [seq_len, d_model] # 位置信息(正弦编码)
=
Input [seq_len, d_model] # 完整的输入表示5.7.3 核心认知
Positional Encoding 解决了 Transformer 的"位置盲"问题。通过把位置向量加到 Embedding 上,模型能够区分同一个词在不同位置的含义,理解"我爱你"和"你爱我"的区别。
本章交付物
学完这一章,你应该能够:
- 解释为什么 Transformer 需要位置编码
- 理解正弦位置编码的基本原理(sin/cos 函数)
- 说明 Embedding 和 Position 是如何结合的
- 区分"可学习位置编码"和"固定正弦编码"
下一章预告
现在我们的输入已经完整了:语义信息(Embedding)+ 位置信息(Position)。
下一章,我们来学习两个重要的数学工具:LayerNorm(层归一化) 和 Softmax。它们在 Transformer 中无处不在,理解它们是理解整个架构的基础。