一句话总结:LayerNorm 让数字保持在合理范围(均值为 0,方差为 1),Softmax 把任意数字变成概率分布(总和为 100%)。这两个工具在 Transformer 中无处不在。
6.1 为什么需要这两个工具?

在 Transformer 的架构中,有两个数学工具反复出现:
- LayerNorm:出现在每个 Block 中,负责"数字缩放"
- Softmax:出现在 Attention 计算和最终输出中,负责"数字变概率"
这一章,我们用最直观的方式理解它们的作用。
6.2 LayerNorm:数字缩放
6.2.1 问题:数字会"爆炸"
神经网络的计算过程中,数字会不断变化。经过多层计算后,数字可能变得非常大或非常小:
- 太大:比如 10000、100000,会导致计算溢出
- 太小:比如 0.0001、0.00001,会导致精度丢失
这就像一个人的体重记录:如果用克为单位,数字会很大(70000g);如果用吨为单位,数字会很小(0.07t)。我们需要一个合适的"标尺"。
6.2.2 解决方案:归一化
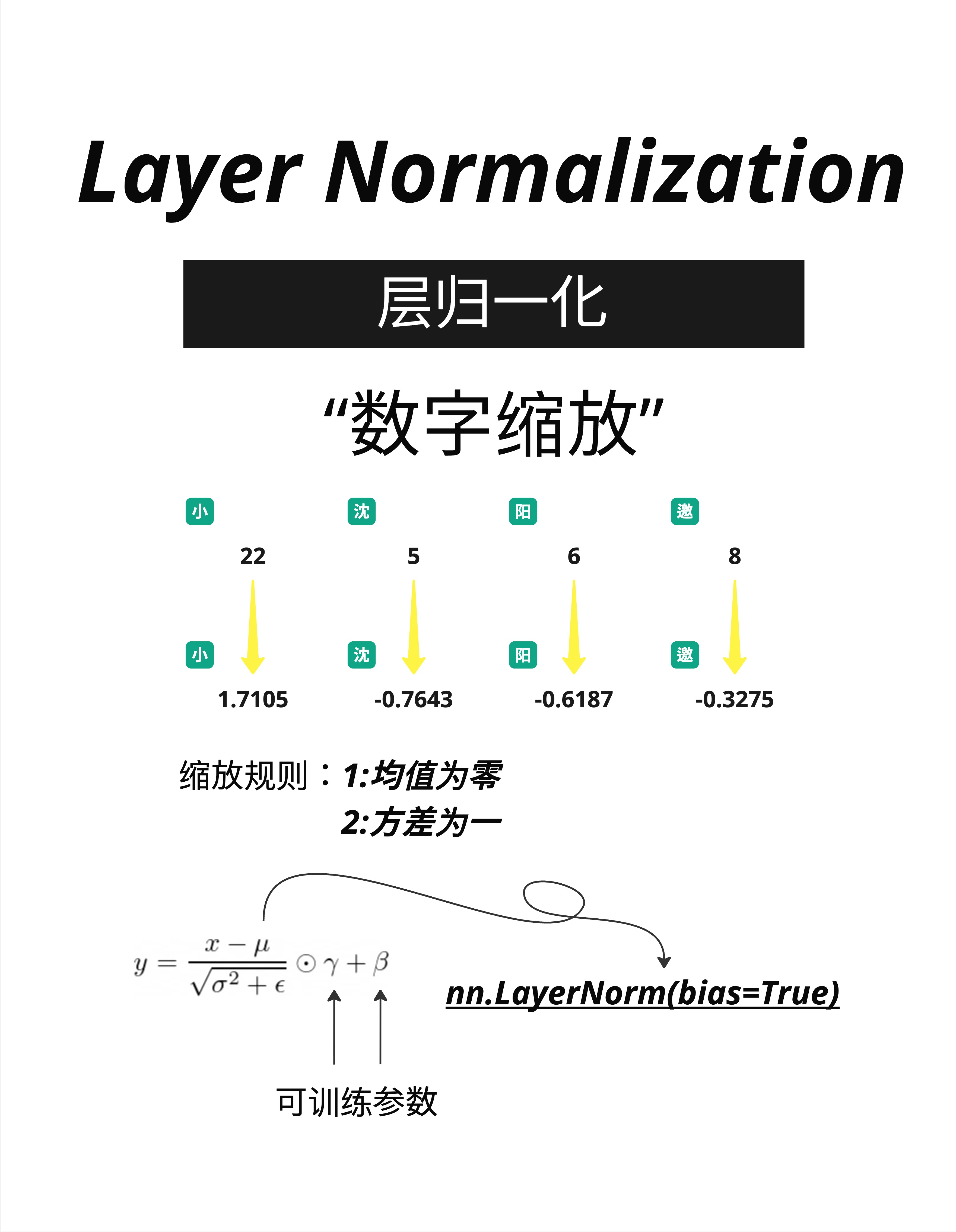
Layer Normalization(层归一化) 的作用就是把数字"缩放"到一个标准范围。
看图中的例子:
输入:小=22, 沈=5, 阳=6, 邀=8
这些数字大小不一,范围从 5 到 22。
输出:小=1.7105, 沈=-0.7643, 阳=-0.6187, 邀=-0.3275
经过 LayerNorm 后,数字被缩放到一个更紧凑的范围。
6.2.3 缩放规则
LayerNorm 遵循两个简单的规则:
- 均值为零:所有数字的平均值变成 0
- 方差为一:数字的"分散程度"变成 1
用公式表示:
y = (x - μ) / √(σ² + ε) × γ + β别被公式吓到,我们拆解一下:
x - μ:每个数字减去平均值(让均值变成 0)/ √(σ² + ε):除以标准差(让方差变成 1)× γ + β:可学习的参数,允许模型调整最终范围
6.2.4 手算示例
假设输入是 [22, 5, 6, 8]:
第一步:计算均值
μ = (22 + 5 + 6 + 8) / 4 = 41 / 4 = 10.25第二步:计算方差
σ² = ((22-10.25)² + (5-10.25)² + (6-10.25)² + (8-10.25)²) / 4
= (138.06 + 27.56 + 18.06 + 5.06) / 4
= 47.19第三步:标准化
小: (22 - 10.25) / √47.19 = 11.75 / 6.87 ≈ 1.71
沈: (5 - 10.25) / √47.19 = -5.25 / 6.87 ≈ -0.76
阳: (6 - 10.25) / √47.19 = -4.25 / 6.87 ≈ -0.62
邀: (8 - 10.25) / √47.19 = -2.25 / 6.87 ≈ -0.33结果:[1.71, -0.76, -0.62, -0.33],均值约为 0,方差约为 1。
6.2.5 PyTorch 实现
# 代码示例
import torch
import torch.nn as nn
# 创建 LayerNorm 层
layer_norm = nn.LayerNorm(normalized_shape=4, bias=True)
# 输入数据
x = torch.tensor([[22.0, 5.0, 6.0, 8.0]])
# 应用 LayerNorm
y = layer_norm(x)
print(y) # 输出接近 [1.71, -0.76, -0.62, -0.33]6.2.6 为什么叫"Layer"Norm?
因为归一化是在每一层的输出上独立进行的。每个 token 的向量单独归一化,不同 token 之间不相互影响。
还有一种叫 Batch Normalization,是在 batch 维度上归一化。但 Transformer 主要使用 Layer Normalization,因为它更适合处理变长序列。
6.3 Softmax:数字变概率
6.3.1 问题:需要概率分布
在很多场景下,我们需要把一组数字转换成概率:
- 预测下一个词:词表中每个词的概率是多少?
- Attention 权重:每个位置应该分配多少注意力?
概率有两个要求:
- 每个值都在 0 到 1 之间
- 所有值加起来等于 1(100%)
6.3.2 解决方案:Softmax
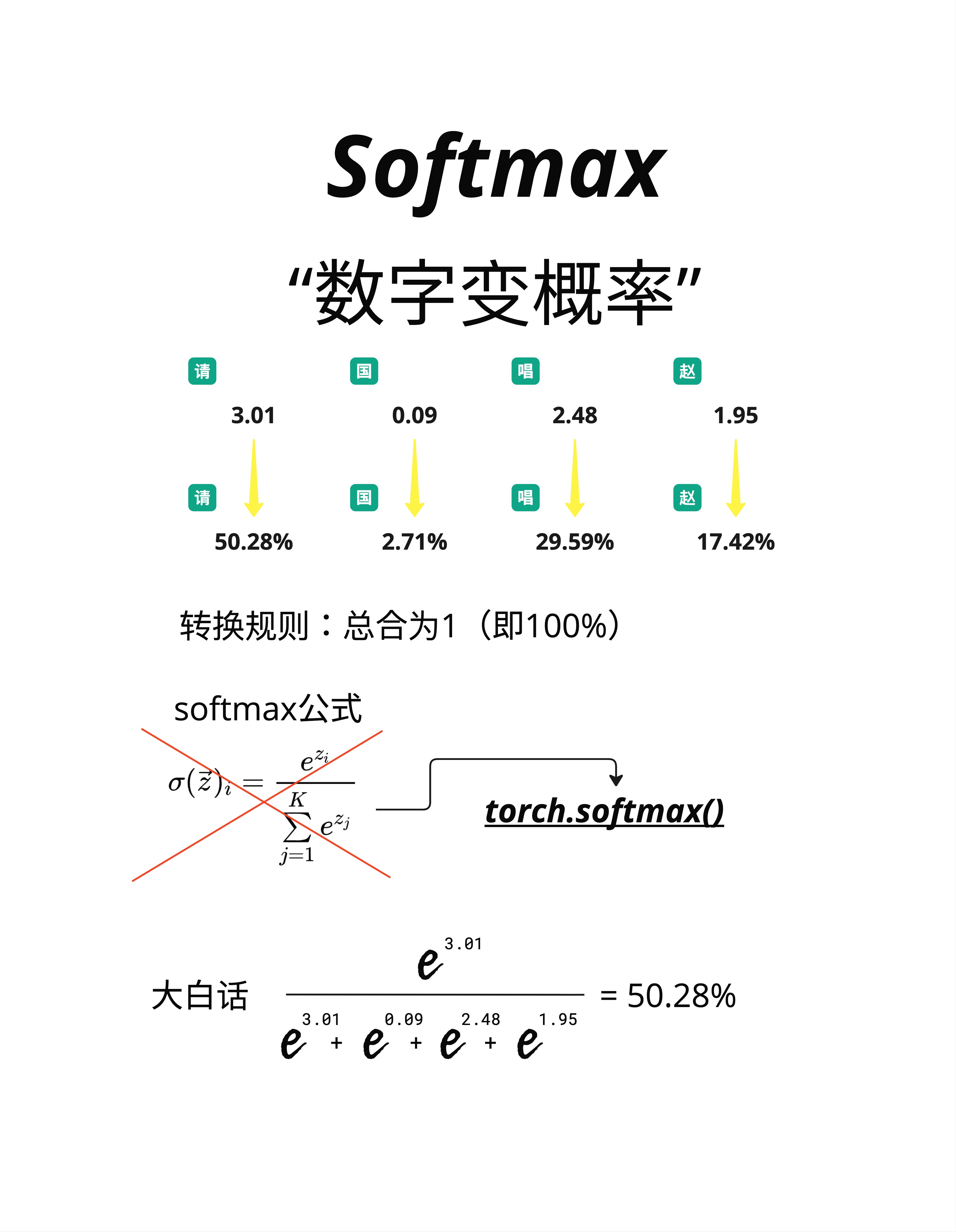
Softmax 函数可以把任意一组数字转换成概率分布。
看图中的例子:
输入(称为 logits):请=3.01, 国=0.09, 唱=2.48, 赵=1.95
这些数字可正可负,大小不一。
输出(概率):请=50.28%, 国=2.71%, 唱=29.59%, 赵=17.42%
转换后:
- 每个值都在 0-100% 之间
- 所有值加起来 = 50.28 + 2.71 + 29.59 + 17.42 = 100%
6.3.3 Softmax 公式
softmax(z)ᵢ = e^zᵢ / Σⱼ e^zⱼ用大白话说:
- 对每个数字取 e 的指数(e ≈ 2.718)
- 除以所有指数的总和
6.3.4 手算示例
输入:[3.01, 0.09, 2.48, 1.95]
第一步:计算 e 的指数
e^3.01 = 20.29
e^0.09 = 1.09
e^2.48 = 11.94
e^1.95 = 7.03第二步:计算总和
总和 = 20.29 + 1.09 + 11.94 + 7.03 = 40.35第三步:计算概率
请: 20.29 / 40.35 = 0.5028 = 50.28%
国: 1.09 / 40.35 = 0.0271 = 2.71%
唱: 11.94 / 40.35 = 0.2959 = 29.59%
赵: 7.03 / 40.35 = 0.1742 = 17.42%6.3.5 Softmax 的特点
-
放大差异:输入差异越大,输出的概率差距越明显
- 输入 [3, 0, 2, 1] → 差异会被放大
-
保持顺序:最大的输入对应最大的概率
- 3.01 最大 → 50.28% 最高
-
平滑输出:即使输入是负数,输出也是正的概率
6.3.6 PyTorch 实现
# 代码示例
import torch
import torch.nn.functional as F
# 输入数据(logits)
logits = torch.tensor([3.01, 0.09, 2.48, 1.95])
# 应用 Softmax
probs = F.softmax(logits, dim=0)
print(probs) # tensor([0.5028, 0.0271, 0.2959, 0.1742])
print(probs.sum()) # tensor(1.0000)6.4 在架构中的位置
6.4.1 输出文字预测
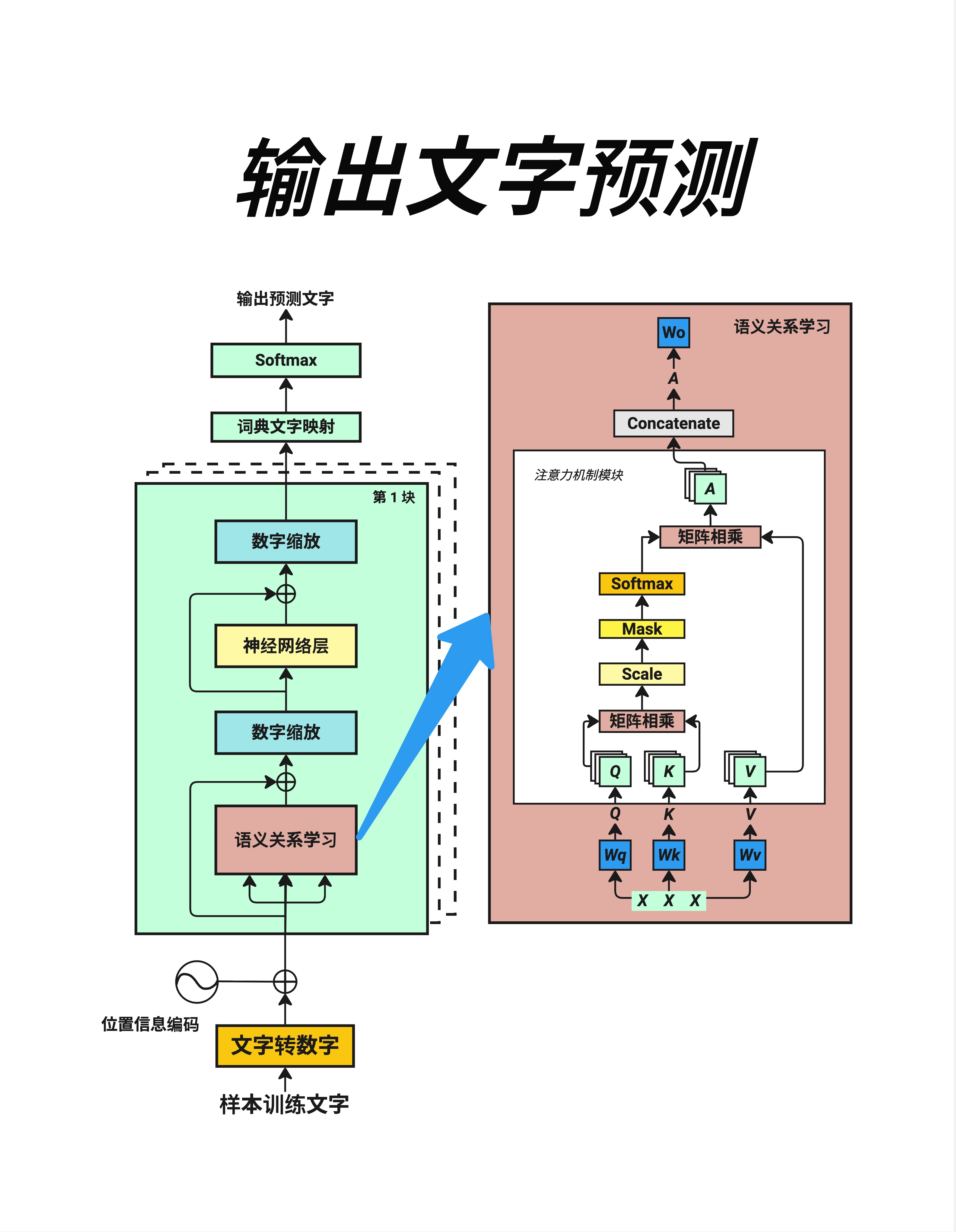
看这张架构图,我们可以清楚地看到 LayerNorm 和 Softmax 的位置:
LayerNorm 的位置(蓝色框"数字缩放"):
- 在 Attention 层之后
- 在 FFN 层之后
- 每个 Block 中出现两次
Softmax 的位置:
- Attention 内部:计算注意力权重时使用
- 最终输出:词典文字映射后,转换成词的概率分布
6.4.2 完整的输出流程
从 Transformer Block 到最终预测:
Block 输出
↓
全部数字列队(所有位置的向量)
↓
词典文字映射(Linear 层,映射到词表大小)
↓
Softmax(转换成概率)
↓
输出预测文字(选择概率最高的词)6.4.3 两者的配合
LayerNorm 和 Softmax 经常配合使用:
- LayerNorm 先把数字稳定在合理范围
- 经过各种计算(Attention、FFN)
- Softmax 最后把结果转换成概率
这种配合保证了:
- 中间计算数值稳定(不会爆炸或消失)
- 最终输出是有效的概率分布
6.5 温度参数(Temperature)
在使用 Softmax 时,有一个重要的参数叫 Temperature(温度)。
6.5.1 温度的作用
softmax(z/T)ᵢ = e^(zᵢ/T) / Σⱼ e^(zⱼ/T)温度 T 控制输出的"确定性":
- T < 1(低温):输出更"尖锐",概率更集中在最大值
- T = 1(标准):正常的 Softmax
- T > 1(高温):输出更"平滑",概率分布更均匀
6.5.2 例子
假设 logits = [3.0, 1.0, 0.5]
| 温度 | 输出概率(近似) | 特点 |
|---|---|---|
| T=0.5 | [0.98, 0.02, 0.01] | 非常确定,几乎只选第一个 |
| T=1.0 | [0.82, 0.11, 0.07] | 标准分布 |
| T=2.0 | [0.60, 0.22, 0.17] | 更均匀,不太确定 |
注:数值经 softmax(logits/T) 计算得出,四舍五入到两位小数。
6.5.3 在 LLM 中的应用
当你使用 ChatGPT 时,可以调整 temperature 参数:
- temperature=0:输出最确定,每次结果相同(确定性解码)
- temperature=0.7:平衡创造性和一致性(常用值)
- temperature=1.0+:更有创造性,但可能更随机
6.6 本章总结
6.6.1 核心概念对比
| 特性 | LayerNorm | Softmax |
|---|---|---|
| 作用 | 数字缩放 | 数字变概率 |
| 输出范围 | 均值=0, 方差=1 | 0~1, 总和=1 |
| 目的 | 稳定训练 | 生成概率分布 |
| 位置 | 每个 Block 中 | Attention 内 + 最终输出 |
6.6.2 公式速记
LayerNorm:
y = (x - 均值) / 标准差 × γ + βSoftmax:
P(i) = e^xᵢ / Σ e^xⱼ6.6.3 核心认知
LayerNorm 是 Transformer 的"稳定器",让数字保持在合理范围;Softmax 是"概率转换器",把任意数字变成概率分布。这两个简单的数学工具,是整个架构稳定运行的基础。
本章交付物
学完这一章,你应该能够:
- 解释 LayerNorm 的作用(均值为 0,方差为 1)
- 手算简单的 Softmax(e 的指数除以总和)
- 说出 LayerNorm 和 Softmax 在 Transformer 中的位置
- 理解 Temperature 参数对输出的影响
下一章预告
LayerNorm 和 Softmax 是两个数学工具。下一章,我们来聊一个更核心的组件:神经网络层(Feed Forward Network)。
它是 Transformer Block 中除了 Attention 之外的另一个主角。好消息是——理解 Transformer 并不需要深入神经网络的细节,我们会用最直观的方式来解释。