一句话总结:神经网络本质上就是矩阵乘法加激活函数。理解 Transformer 不需要深入神经网络细节,只需要知道它是一个"输入 → 处理 → 输出"的黑盒子。
7.1 先说结论:你不需要"懂"神经网络

在深入之前,我想先打消你的顾虑:
理解 Transformer 和大模型,不需要成为神经网络专家。
为什么?因为神经网络在 Transformer 中扮演的角色其实很简单——就是一个"处理器",把输入变成输出。你需要知道的是:
- 输入是什么形状
- 输出是什么形状
- 中间有一些可学习的参数
至于里面具体怎么算的?对于理解 Transformer 来说,可以当作黑盒子。
当然,如果你想深入了解,这一章也会给你足够的直觉。
7.2 神经网络的灵感:人脑
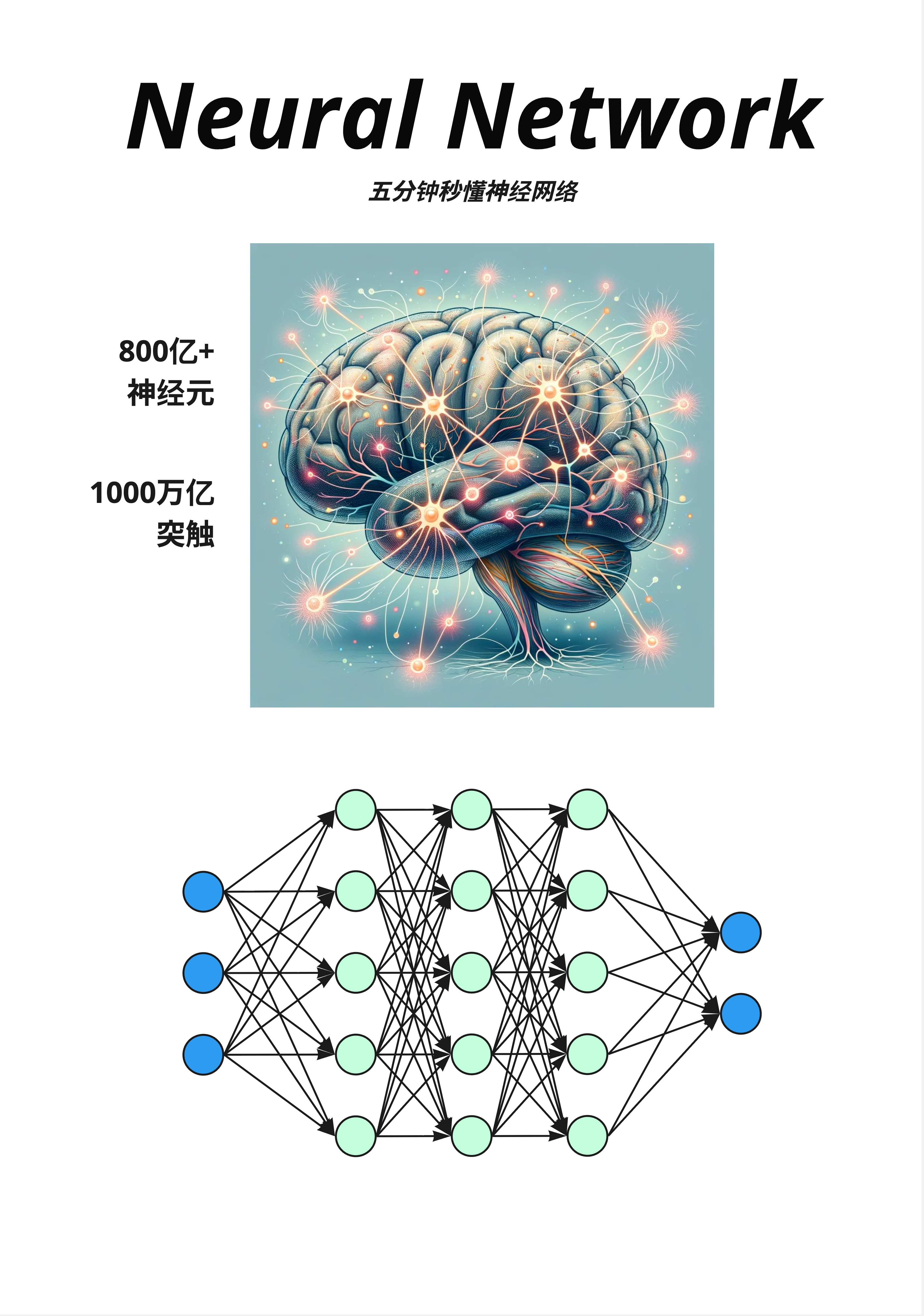
7.2.1 生物神经网络
人脑是世界上最复杂的"计算机":
- 800 亿+神经元:每个神经元都是一个小的处理单元
- 1000 万亿突触:神经元之间的连接
神经元通过电信号相互传递信息。当一个神经元接收到足够多的输入信号时,它会"激活"并向下游神经元发送信号。
7.2.2 人工神经网络
人工神经网络(Artificial Neural Network)是对生物神经网络的简化模拟:
- 节点:模拟神经元
- 连接:模拟突触,每个连接有一个"权重"
- 激活:当输入超过阈值时,节点被激活
但请注意:人工神经网络和真正的大脑差别很大。它只是借用了"神经网络"这个名字,实际上是一种数学模型。
7.3 神经网络能做什么?

7.3.1 学习"特征"
神经网络的神奇之处在于:它能自动学习数据的"特征"。
看这张图(MNIST 手写数字可视化):
- 10000 个点,每个点是一张手写数字图片
- 784 维(28×28 像素)的图片被压缩到 2D 显示
- 相同的数字自动聚集在一起!
0 聚在一起,1 聚在一起,2 聚在一起...
没有人告诉神经网络"0 长这样"、"1 长这样"。它通过训练数据自己学会了区分不同数字的特征。
7.3.2 这和 LLM 有什么关系?
同样的原理用在语言上:
- 神经网络学会了哪些词经常一起出现
- 学会了句子的语法结构
- 学会了词语的语义关系
最终,"国王"和"王后"的向量会很接近,而"国王"和"苹果"会很远——就像图中相同数字聚在一起一样。
7.4 神经网络的基本结构
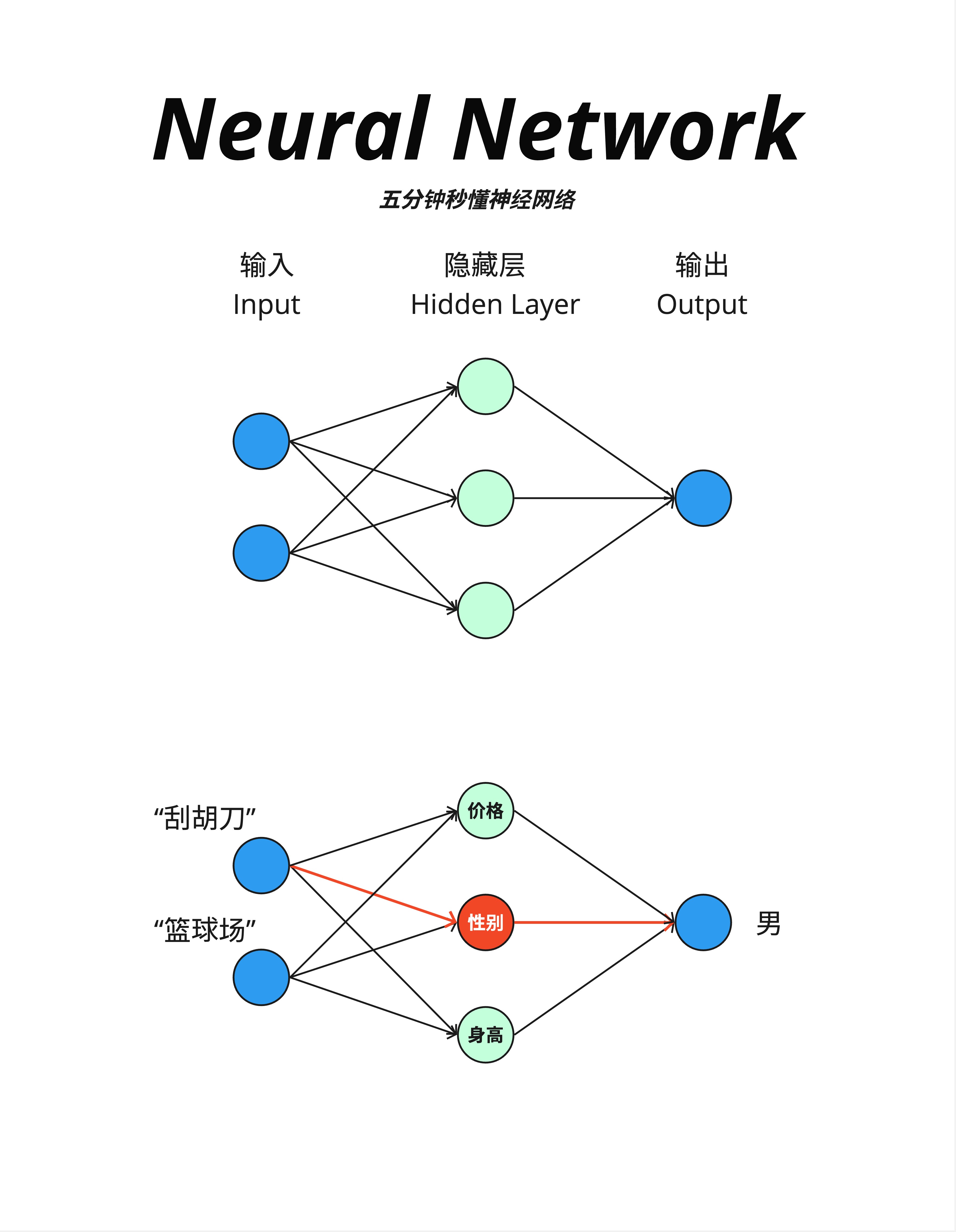
7.4.1 三层结构
最简单的神经网络有三层:
- 输入层(Input):接收原始数据
- 隐藏层(Hidden Layer):进行计算处理
- 输出层(Output):产生结果
7.4.2 一个直观的例子
图中下半部分展示了一个有趣的例子:
输入:
- "刮胡刀" → 一个向量
- "篮球场" → 一个向量
隐藏层的特征:
- 价格
- 性别(红色高亮)
- 身高
输出:
- "男"
神经网络学会了:刮胡刀和篮球场都和"男性"相关,所以输出"男"。
这就是神经网络的本质:从输入中提取特征,然后做出判断。
7.5 数学本质:矩阵乘法
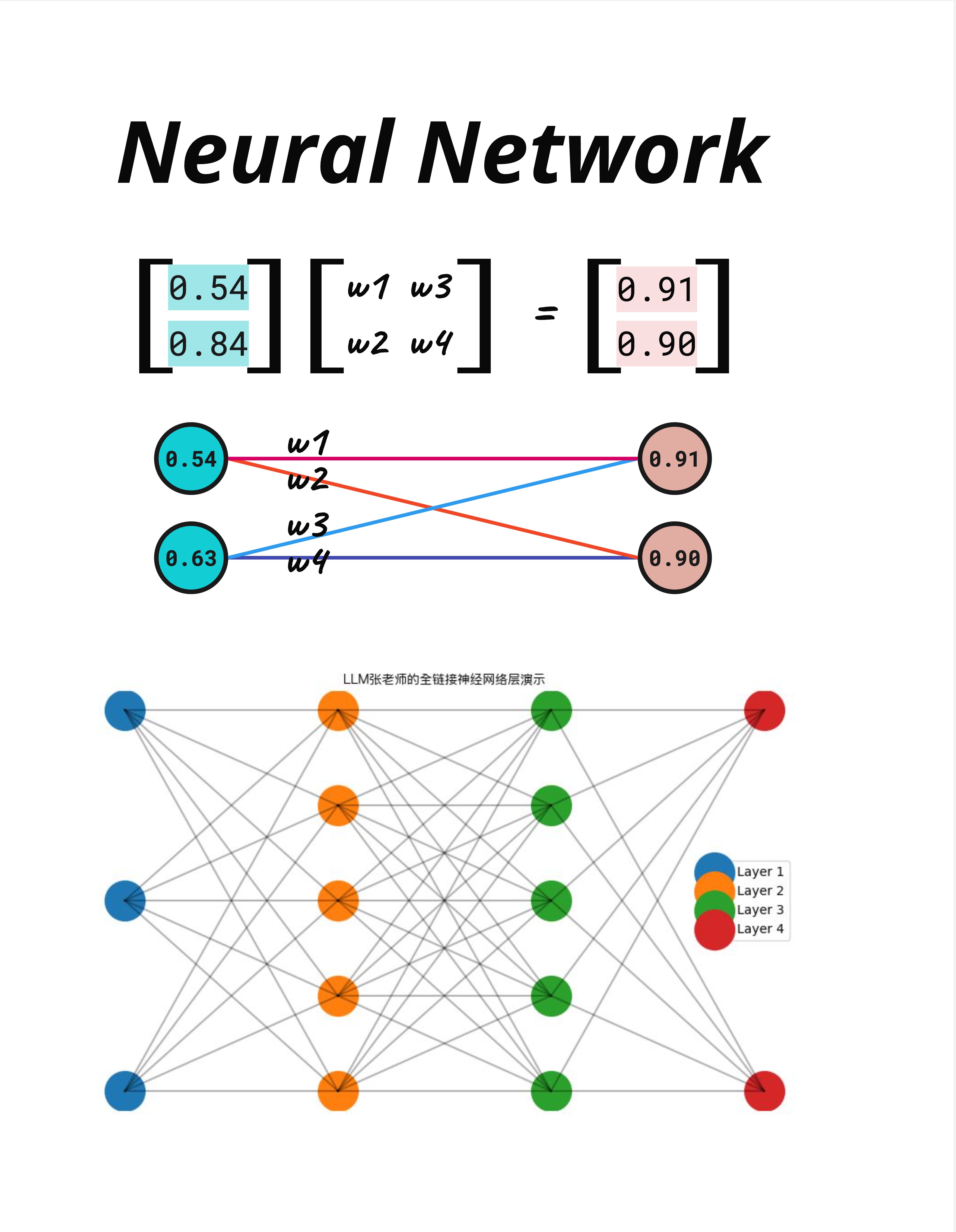
7.5.1 一切都是矩阵乘法
神经网络的核心计算其实非常简单:矩阵乘法。
看图中的例子:
输入向量 × 权重矩阵 = 输出向量
[0.54] [w1 w3] [0.91]
[0.84] × [w2 w4] = [0.90]就这么简单。输入是一个向量,乘以一个权重矩阵,得到输出向量。
7.5.2 可视化理解
图中下方展示了同样的过程用"网络图"表示:
- 左边两个蓝色节点(0.54, 0.63)是输入
- 右边两个粉色节点(0.91, 0.90)是输出
- 中间的线是权重(w1, w2, w3, w4)
每个输出节点的值 = 所有输入 × 对应权重的总和。
7.5.3 多层神经网络
图中最下方展示了一个多层网络(LLM张老师的全链接神经网络层演示):
- Layer 1(蓝色)→ Layer 2(橙色)→ Layer 3(绿色)→ Layer 4(红色)
- 每一层到下一层,都是一次矩阵乘法
- 层数越多,网络越"深"(这就是"深度学习"名字的由来)
7.6 PyTorch 实现
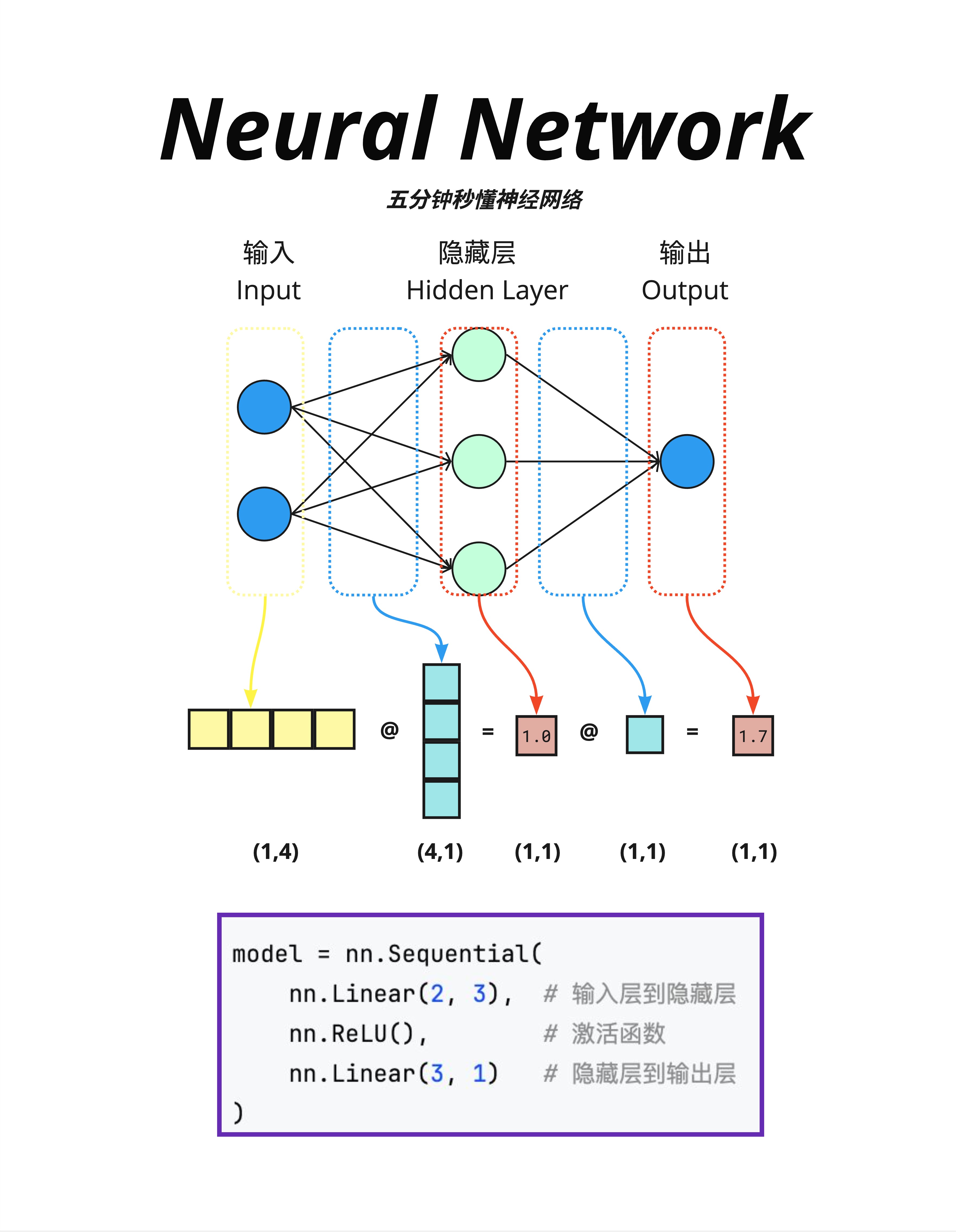
7.6.1 代码示例
# 代码示例
import torch.nn as nn
model = nn.Sequential(
nn.Linear(2, 3), # 输入层到隐藏层:2维 → 3维
nn.ReLU(), # 激活函数
nn.Linear(3, 1) # 隐藏层到输出层:3维 → 1维
)这段代码定义了一个简单的神经网络:
nn.Linear(2, 3):一个线性层,把 2 维输入变成 3 维输出nn.ReLU():激活函数,增加非线性nn.Linear(3, 1):把 3 维变成 1 维输出
7.6.2 矩阵维度变化
图中展示了维度变化:
输入 (1,4) @ 权重 (4,1) = 中间结果 (1,1) @ 权重 (1,1) = 输出 (1,1)理解维度变化是理解神经网络的关键:
(1,4):1 个样本,4 个特征(4,1):权重矩阵,把 4 维变成 1 维- 矩阵乘法规则:
(a,b) @ (b,c) = (a,c)
7.6.3 激活函数
你可能注意到了 nn.ReLU()。这是激活函数,它的作用是增加"非线性"。
如果没有激活函数,多层矩阵乘法可以合并成一层(线性变换的组合还是线性变换)。激活函数让网络能学习更复杂的模式。
ReLU 是最常用的激活函数,规则很简单:
ReLU(x) = max(0, x)正数不变,负数变成 0。
7.7 在 Transformer 中的神经网络
7.7.1 Feed Forward Network
在 Transformer 中,神经网络层被称为 Feed Forward Network(FFN,前馈网络) 或 全链接网络层。
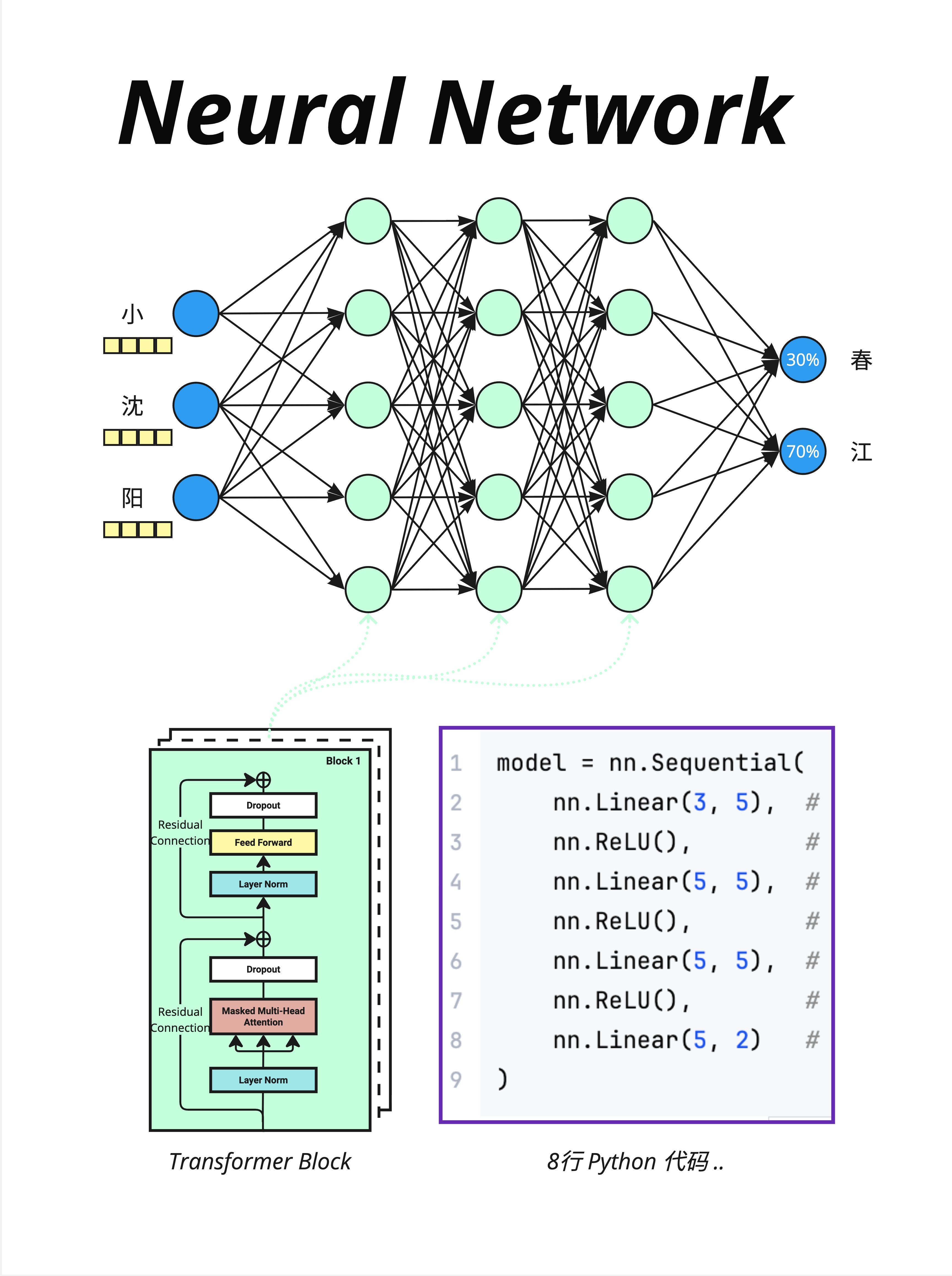
看图中的例子:
输入:小、沈、阳(三个 token 的向量) FFN 输出:每个 token 的新向量表示(维度不变)
注意:图中显示的"春=30%、江=70%"概率分布,实际上是由**最后的 LM Head(线性层 + Softmax)**产生的,而不是 FFN 本身。FFN 只是在处理和转换向量表示。
7.7.2 Transformer Block 结构
图中左下角展示了 Transformer Block 的结构:
Layer Norm
↓
Masked Multi-Head Attention
↓
Dropout + 残差连接
↓
Layer Norm
↓
Feed Forward(神经网络层)← 就是这里!
↓
Dropout + 残差连接Feed Forward 是每个 Block 的重要组成部分,和 Attention 交替出现。
7.7.3 简化的代码
图中右侧展示了简化的 PyTorch 代码:
model = nn.Sequential(
nn.Linear(3, 5), # 第1层
nn.ReLU(),
nn.Linear(5, 5), # 第2层
nn.ReLU(),
nn.Linear(5, 5), # 第3层
nn.ReLU(),
nn.Linear(5, 2) # 输出层
)8 行代码,就定义了一个神经网络!这就是为什么我们说"大模型就是两个文件"——代码真的很简洁。
7.8 参数都在哪里?
7.8.1 哪些地方有参数?
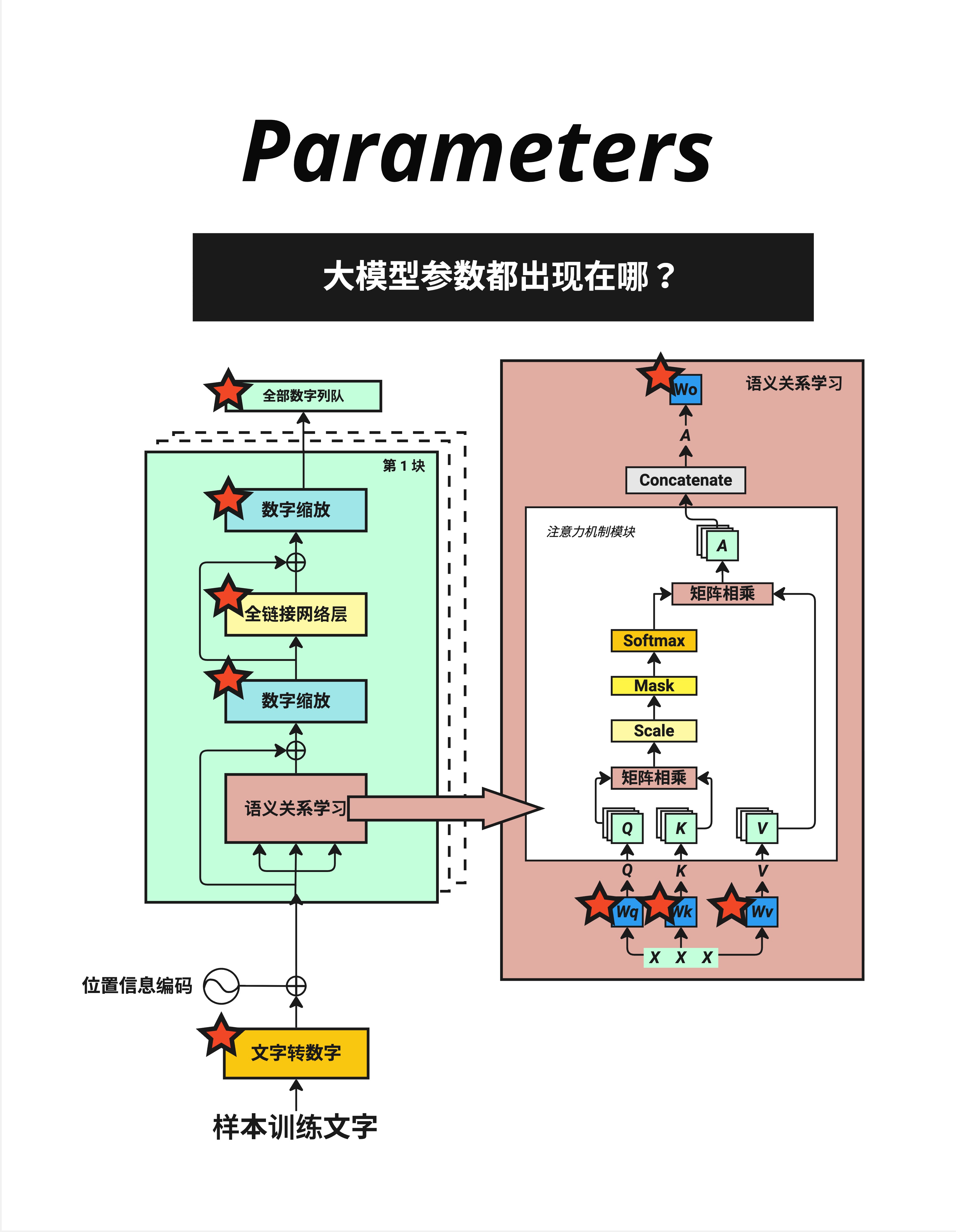
看这张图,红色星星标注了所有有参数的地方:
- 文字转数字(Embedding):词表大小 × 向量维度
- 全链接网络层(FFN):输入维度 × 输出维度
- 数字缩放(LayerNorm):γ 和 β 参数
- 语义关系学习(Attention):Wq、Wk、Wv、Wo 四个权重矩阵
- 全部数字列队(最终 Linear):向量维度 × 词表大小
7.8.2 参数量估算
对于一个典型的 Transformer:
| 组件 | 参数量公式 | LLaMA-7B 示例 |
|---|---|---|
| Embedding | vocab × d_model | 32000 × 4096 ≈ 1.3亿 |
| FFN(每层) | 3 × d_model × d_ff * | 3 × 4096 × 11008 ≈ 1.35亿 |
| Attention(每层) | 4 × d_model² | 4 × 4096² ≈ 0.67亿 |
| LayerNorm(每层) | 2 × d_model | 2 × 4096 ≈ 8K(很少) |
*LLaMA 使用 SwiGLU 激活函数,需要 3 个矩阵(gate、up、down),而非传统 FFN 的 2 个矩阵。
FFN 占了大部分参数! 这是一个常被忽视的事实。
7.8.3 一个有趣的观察
很多人以为 Attention 是 Transformer 的"主角",参数最多。但实际上:
- FFN 的参数量通常是 Attention 的 2-3 倍
- Attention 的强项是"理解关系",FFN 的强项是"存储知识"
有研究认为,模型的"知识"主要存储在 FFN 的权重中。
7.9 本章总结
7.9.1 核心认知
| 概念 | 解释 |
|---|---|
| 神经网络 | 输入 → 矩阵乘法 → 激活函数 → 输出 |
| 层 | 每一次矩阵乘法 + 激活函数 |
| 参数 | 矩阵中的数字,通过训练学习 |
| FFN | Transformer 中的神经网络层 |
7.9.2 记住这个公式
神经网络的本质:
输出 = 激活函数(输入 × 权重 + 偏置)用 PyTorch 表示:
nn.Linear(in_features, out_features) # 线性层
nn.ReLU() # 激活函数7.9.3 你只需要知道的
- 形状变化:神经网络改变向量的维度
- 可学习参数:权重矩阵是训练出来的
- FFN 的位置:在每个 Transformer Block 中,和 Attention 交替出现
- FFN 很重要:它存储了模型的大部分参数和"知识"
神经网络就是矩阵乘法的堆叠。理解 Transformer 不需要深入神经网络的细节,把它当作一个"处理器"就够了:输入向量进去,输出向量出来。
本章交付物
学完这一章,你应该能够:
- 解释神经网络的基本结构(输入层、隐藏层、输出层)
- 理解神经网络本质是矩阵乘法
- 知道 FFN 在 Transformer Block 中的位置
- 了解参数主要分布在哪些组件中
Part 2 总结
恭喜你完成了 Part 2:核心组件!
让我们回顾一下学到的内容:
| 章节 | 组件 | 核心作用 |
|---|---|---|
| 第4章 | Tokenization + Embedding | 文字 → Token ID → 向量 |
| 第5章 | Positional Encoding | 给向量添加位置信息 |
| 第6章 | LayerNorm + Softmax | 数字缩放 + 数字变概率 |
| 第7章 | 神经网络层(FFN) | 处理和存储知识 |
现在你已经理解了 Transformer 的所有"配件"。下一个 Part,我们将进入最核心的部分:Attention 机制——Transformer 真正的灵魂。
下一章预告
Part 3 的第一章(第 8 章),我们要先补一个数学基础:线性变换的几何意义。
这是理解 Attention 的关键。我们会用可视化的方式,让你真正"看懂"矩阵乘法在做什么。
准备好了吗?让我们进入 Attention 的世界!