一句话总结：Attention 机制的核心是用点积计算"相似度"——找出句子中哪些词和当前词最相关，然后把注意力集中在那里。这就是 Transformer 理解语言的秘密武器。

9.1 回顾：我们已经知道什么

在进入 Attention 之前，让我们回顾一下前面学到的内容：

章节	学到的概念	核心作用
第4章	Tokenization + Embedding	文字 → Token ID → 向量
第5章	Positional Encoding	给向量添加位置信息
第6章	LayerNorm + Softmax	数字缩放 + 数字变概率
第7章	神经网络层（FFN）	处理和存储知识
第8章	线性变换	矩阵乘法 = 计算相似度/投影

现在，我们终于要进入 Transformer 最核心的部分：Attention（注意力机制）。

9.2 Attention 在架构中的位置

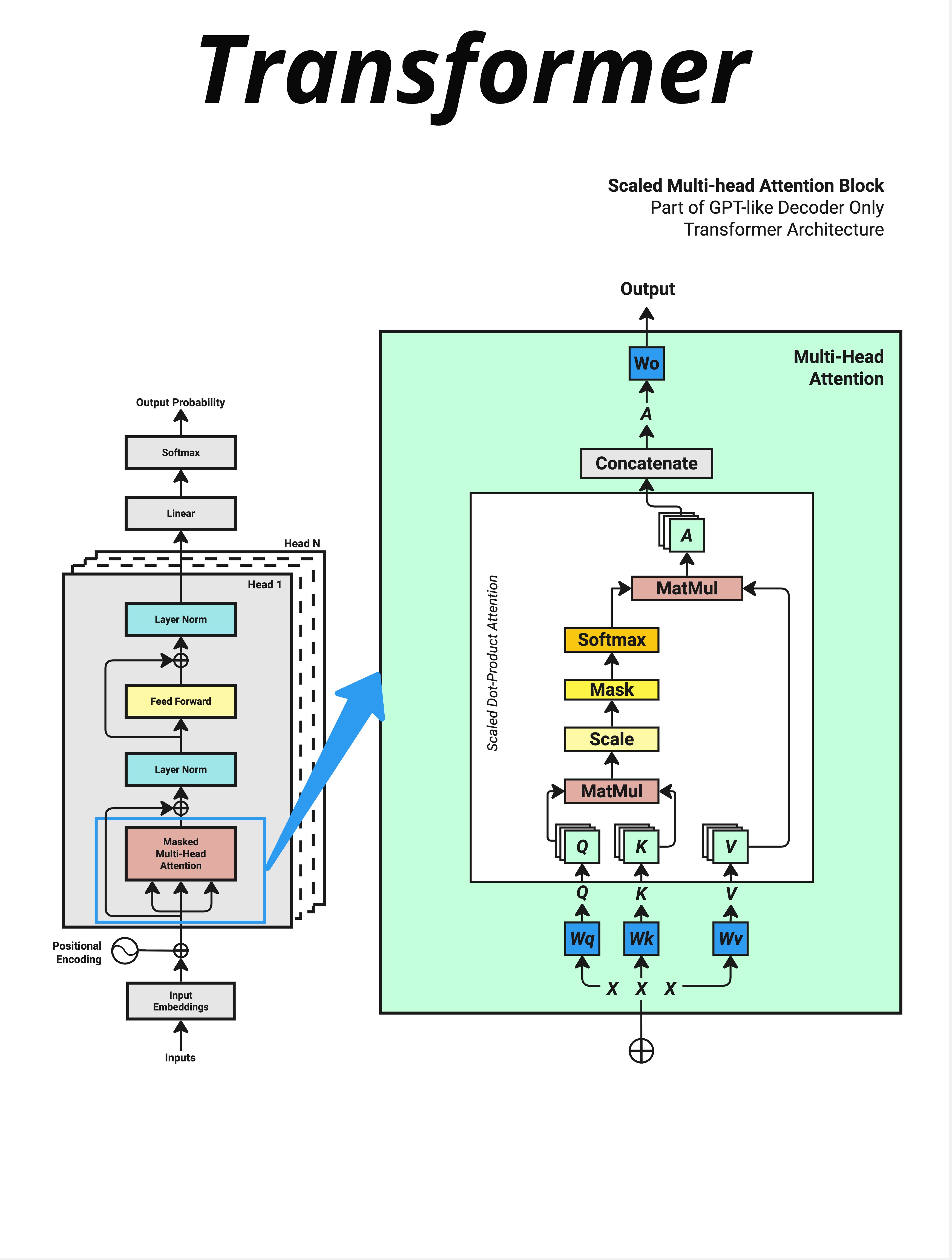
看这张图，左边是完整的 Transformer 架构，右边是 Multi-Head Attention 的内部结构。

9.2.1 Transformer Block 的结构

每个 Transformer Block 包含两个主要部分：

输入
  ↓
Layer Norm
  ↓
Masked Multi-Head Attention  ← 这就是我们要学的！
  ↓
残差连接 + Dropout
  ↓
Layer Norm
  ↓
Feed Forward（FFN）
  ↓
残差连接 + Dropout
  ↓
输出

Attention 是每个 Block 的第一个核心组件，它负责让模型"理解"词与词之间的关系。

9.2.2 Attention 的内部流程

右边的绿色框展示了 Scaled Dot-Product Attention 的完整流程：

输入 X
  ↓
生成 Q, K, V（通过 Wq, Wk, Wv 三个权重矩阵）
  ↓
MatMul（Q @ K^T，计算相似度）
  ↓
Scale（除以 √d_key，缩放）
  ↓
Mask（遮挡未来信息，仅在 Decoder 中使用）
  ↓
Softmax（转换为概率分布）
  ↓
MatMul（与 V 相乘，加权求和）
  ↓
Concatenate（多头合并）
  ↓
Wo（输出投影）
  ↓
输出

这一章，我们先建立 Attention 的几何直觉，理解为什么要用点积。下一章再详细讲 Q、K、V 是什么。

9.3 为什么需要 Attention？

9.3.1 语言理解的核心问题

考虑这个句子：

"小沈阳江西演唱会邀请了，"

当模型要预测下一个词时，它需要理解：

"邀请了"后面应该跟什么？
是"谁"被邀请？还是"邀请了谁"？
"小沈阳"和"邀请"有什么关系？
"江西演唱会"是地点还是事件？

每个词的含义，都依赖于它和其他词的关系。

9.3.2 传统方法的局限

在 Transformer 之前，处理序列的主流方法是 RNN（循环神经网络）：

词1 → 词2 → 词3 → 词4 → 词5 → ...
      ↘    ↘    ↘    ↘
      隐状态传递

RNN 的问题：

顺序处理：必须一个词一个词地处理，无法并行
长距离依赖：信息在传递过程中会衰减，很难记住很远的词
计算效率低：序列越长，计算时间越长

9.3.3 Attention 的解决方案

Attention 的核心思想是：让每个词都能直接"看到"所有其他词。

        词1  词2  词3  词4  词5
词1      ↔    ↔    ↔    ↔    ↔
词2      ↔    ↔    ↔    ↔    ↔
词3      ↔    ↔    ↔    ↔    ↔
词4      ↔    ↔    ↔    ↔    ↔
词5      ↔    ↔    ↔    ↔    ↔

每个词都可以和所有其他词建立联系，不需要通过中间状态传递。

这就像一个班级讨论：

RNN 模式：传话游戏，信息从第一个人传到最后一个人
Attention 模式：圆桌会议，每个人都能直接听到所有人的发言

9.4 点积：计算"相似度"的工具

9.4.1 回顾第8章的核心结论

在第8章，我们学到了点积的几何意义：

点积 = 余弦相似度 × 向量长度

两个向量的点积越大，说明它们的方向越接近，越"相似"。

这正是 Attention 需要的！

9.4.2 用点积找"相关的词"

假设每个词都有一个向量表示：

小    = [0.2, 0.8, 0.3, ...]
沈    = [0.3, 0.7, 0.4, ...]
阳    = [0.1, 0.9, 0.2, ...]
邀请  = [0.8, 0.2, 0.7, ...]

当我们想知道"邀请"和哪个词最相关时，可以计算点积：

邀请 · 小 = 0.8×0.2 + 0.2×0.8 + 0.7×0.3 = 0.53
邀请 · 沈 = 0.8×0.3 + 0.2×0.7 + 0.7×0.4 = 0.66
邀请 · 阳 = 0.8×0.1 + 0.2×0.9 + 0.7×0.2 = 0.40

结果显示"邀请"和"沈"的相似度最高（0.66），其次是"小"（0.53），最后是"阳"（0.40）。

9.4.3 矩阵乘法：批量计算所有相似度

如果要计算所有词两两之间的相似度，一个个算太慢了。

用矩阵乘法，一次搞定！

词向量矩阵 [n, d] @ 词向量矩阵转置 [d, n] = 相似度矩阵 [n, n]

结果是一个 n×n 的矩阵，其中位置 (i, j) 表示第 i 个词和第 j 个词的相似度。

9.5 Attention 热力图：可视化理解

9.5.1 Q @ K 的结果

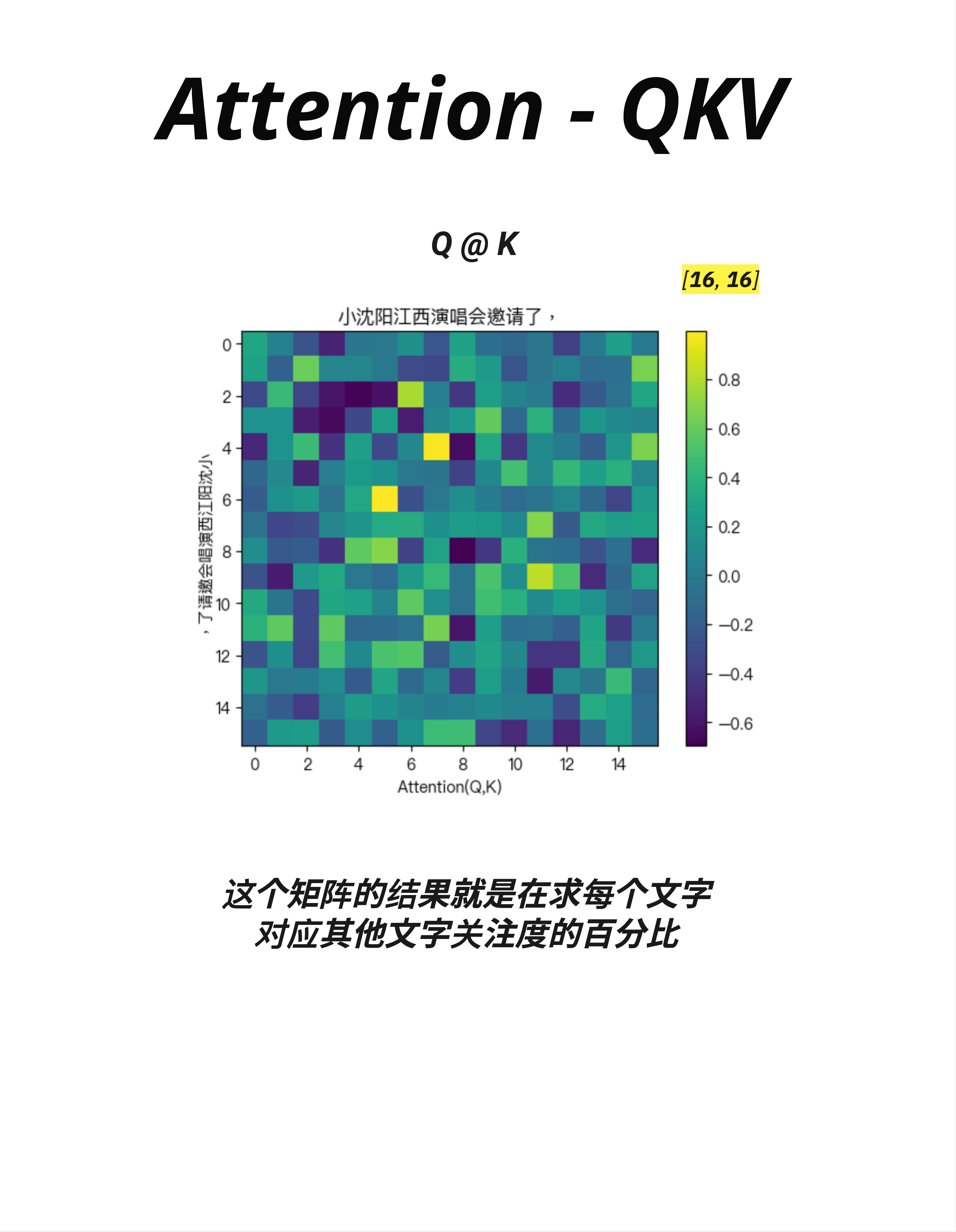
这张图展示了 Q @ K 的计算结果——一个 16×16 的注意力矩阵。

输入句子是："小沈阳江西演唱会邀请了，"（16 个 token）

9.5.2 如何解读热力图

横轴（X轴）：Query（查询），表示"谁在问"
纵轴（Y轴）：Key（键），表示"谁被问"
颜色深浅：表示相似度/注意力权重
- 黄色（亮）= 高相似度，高注意力
- 深蓝色（暗）= 低相似度，低注意力

9.5.3 从热力图中能看出什么

观察这张热力图：

对角线较亮：每个词对自己的注意力较高（这很自然）
某些位置特别亮：比如第 4-5 列（对应"阳"附近）有几个亮点，说明多个词都在"关注"这个位置
注意力分布不均匀：不是每个词都平等地关注所有词，而是有选择性地聚焦

核心洞察：这个矩阵的结果就是在求每个文字对应其他文字关注度的百分比。

9.5.4 这就是"注意力"的含义

Attention 的本质：

不是平等对待所有词
而是有选择地关注最相关的词
把"注意力"集中在重要的地方

就像你阅读时，眼睛不是均匀扫过每个字，而是在关键词上停留更久。

9.6 从相似度到注意力权重

9.6.1 问题：原始点积的值范围不确定

直接用点积有一个问题：结果的范围不固定。

点积结果：[3.5, -2.1, 8.7, 0.3, ...]

这些数字：

可正可负
大小不一
无法直接解释为"百分比"

9.6.2 解决方案：Softmax

还记得第6章的 Softmax 吗？它可以把任意数字转换成概率分布！

Softmax([3.5, -2.1, 8.7, 0.3]) = [0.05, 0.00, 0.94, 0.01]

现在结果变成了：

每个值都在 0-1 之间
所有值加起来 = 1（100%）
可以解释为"注意力分配的比例"

9.6.3 Scale：为什么要除以 √d

在 Softmax 之前，还有一个 Scale（缩放） 步骤：

Attention(Q, K, V) = softmax(QK^T / √d_key) × V

为什么要除以 √d_key？

原因：防止点积结果太大

当向量维度很高时（比如 d=512），点积的结果会很大：

512 个数相乘再相加
结果可能是几百甚至几千

这会导致 Softmax 的输出变得极端：

最大值接近 1
其他值接近 0
梯度消失，难以训练

除以 √d_key（比如 √512 ≈ 22.6）可以把结果缩放到合理范围。

9.7 完整的 Attention 公式

9.7.1 公式

\\text{Attention}(Q, K, V) = \\text{softmax}\\left(\\frac{QK^T}{\\sqrt{d_{key}}}\\right) V

9.7.2 拆解理解

让我们一步步理解这个公式：

第一步：Q @ K^T

计算 Query 和 Key 的相似度
结果是一个 [seq_len, seq_len] 的矩阵
每个位置 (i, j) 表示：第 i 个 token 对第 j 个 token 的"关注程度"

第二步：/ √d_key

缩放，防止数值太大
d_key 是 Key 向量的维度

第三步：Softmax

把相似度变成概率分布
每一行加起来等于 1

第四步：× V

用注意力权重对 Value 进行加权求和
结果是"根据注意力分配重新组合"的新表示

9.7.3 一个直观的类比

想象你在图书馆找书：

Query（Q）：你心里想找的内容（"我想找关于机器学习的书"）
Key（K）：每本书的标签/关键词（"Python", "机器学习", "烹饪", ...）
相似度（Q @ K）：你的需求和每本书的匹配程度
Softmax：根据匹配程度分配注意力
Value（V）：每本书的实际内容
输出（Attention × V）：你获取的信息，更多来自匹配度高的书

9.8 为什么点积是最佳选择？

9.8.1 计算效率

点积可以用矩阵乘法高效实现：

# 一行代码计算所有相似度
attention_scores = Q @ K.transpose(-2, -1)

GPU 对矩阵乘法有极致优化，这让 Attention 能够并行处理所有位置。

9.8.2 几何意义清晰

点积 = 余弦相似度 × 向量长度

这给了我们直观的理解：

向量方向相近 → 点积大 → 注意力高
向量方向相反 → 点积负 → 注意力低（Softmax 后接近 0）

9.8.3 可学习的灵活性

虽然点积本身是固定的操作，但 Q、K、V 是通过可学习的权重矩阵（Wq、Wk、Wv）生成的。

这意味着模型可以学习：

什么样的 Query 能找到相关的 Key
如何把原始向量转换成有意义的 Q、K、V

9.9 Self-Attention vs Cross-Attention

9.9.1 Self-Attention（自注意力）

在 GPT 这样的 Decoder-only 模型中，Q、K、V 都来自同一个序列：

输入："小沈阳江西演唱会邀请了，"
Q = 输入 @ Wq
K = 输入 @ Wk
V = 输入 @ Wv

每个词关注的是同一句话中的其他词——这叫 Self-Attention（自注意力）。

9.9.2 Cross-Attention（交叉注意力）

在 Encoder-Decoder 模型（如原始 Transformer、翻译模型）中，Q 来自一个序列，K、V 来自另一个序列：

Encoder 输入："Hello World"
Decoder 输入："你好"

Q = Decoder 输入 @ Wq
K = Encoder 输出 @ Wk
V = Encoder 输出 @ Wv

Decoder 的每个词关注的是 Encoder 中的词——这叫 Cross-Attention（交叉注意力）。

9.9.3 GPT 只用 Self-Attention

GPT 是 Decoder-only 架构，只使用 Self-Attention：

只有一个输入序列
每个词关注自己和之前的词
通过 Mask 防止"偷看"未来的词

9.10 本章总结

9.10.1 核心概念

概念	解释
Attention	让每个词能直接关注所有其他词
点积	计算两个向量相似度的工具
Q @ K	计算所有词两两之间的相似度矩阵
Scale	除以 √d_key，防止数值过大
Softmax	把相似度变成注意力权重（概率分布）
Self-Attention	Q、K、V 来自同一序列

9.10.2 Attention 公式

Attention(Q, K, V) = softmax(QK^T / √d_key) × V

9.10.3 核心认知

Attention 的几何本质是用点积计算"相似度"。通过 Q @ K 找出哪些词和当前词最相关，用 Softmax 把相似度变成注意力权重，最后用这些权重对 V 进行加权求和。这让模型能够动态地把注意力集中在最重要的位置。

本章交付物

学完这一章，你应该能够：

解释为什么 Attention 比 RNN 更适合处理序列
说出点积在 Attention 中的作用（计算相似度）
理解 Attention 热力图的含义
解释为什么要 Scale（除以 √d_key）
区分 Self-Attention 和 Cross-Attention

下一章预告

现在我们理解了 Attention 的几何逻辑——用点积计算相似度。

但还有一个关键问题没回答：Q、K、V 到底是什么？它们是怎么来的？

下一章，我们来详细拆解 Q、K、V 的生成过程，以及它们各自的含义。这是真正理解 Attention 的关键！