一句话总结:Q(Query)是"我在找什么",K(Key)是"我有什么标签",V(Value)是"我的实际内容"。Attention 就是用 Q 去匹配 K,找到相关的 V,然后加权求和得到输出。
10.1 本章目标
上一章我们建立了 Attention 的几何直觉:用点积计算相似度。
但还有几个关键问题没回答:
- Q、K、V 是什么意思?
- 它们是怎么从输入生成的?
- 整个 Attention 的维度变化是怎样的?
这一章,我们来完整追踪 Attention 的计算过程,把每一步的维度变化都搞清楚。
10.2 输入数据的形状
10.2.1 理解输入维度
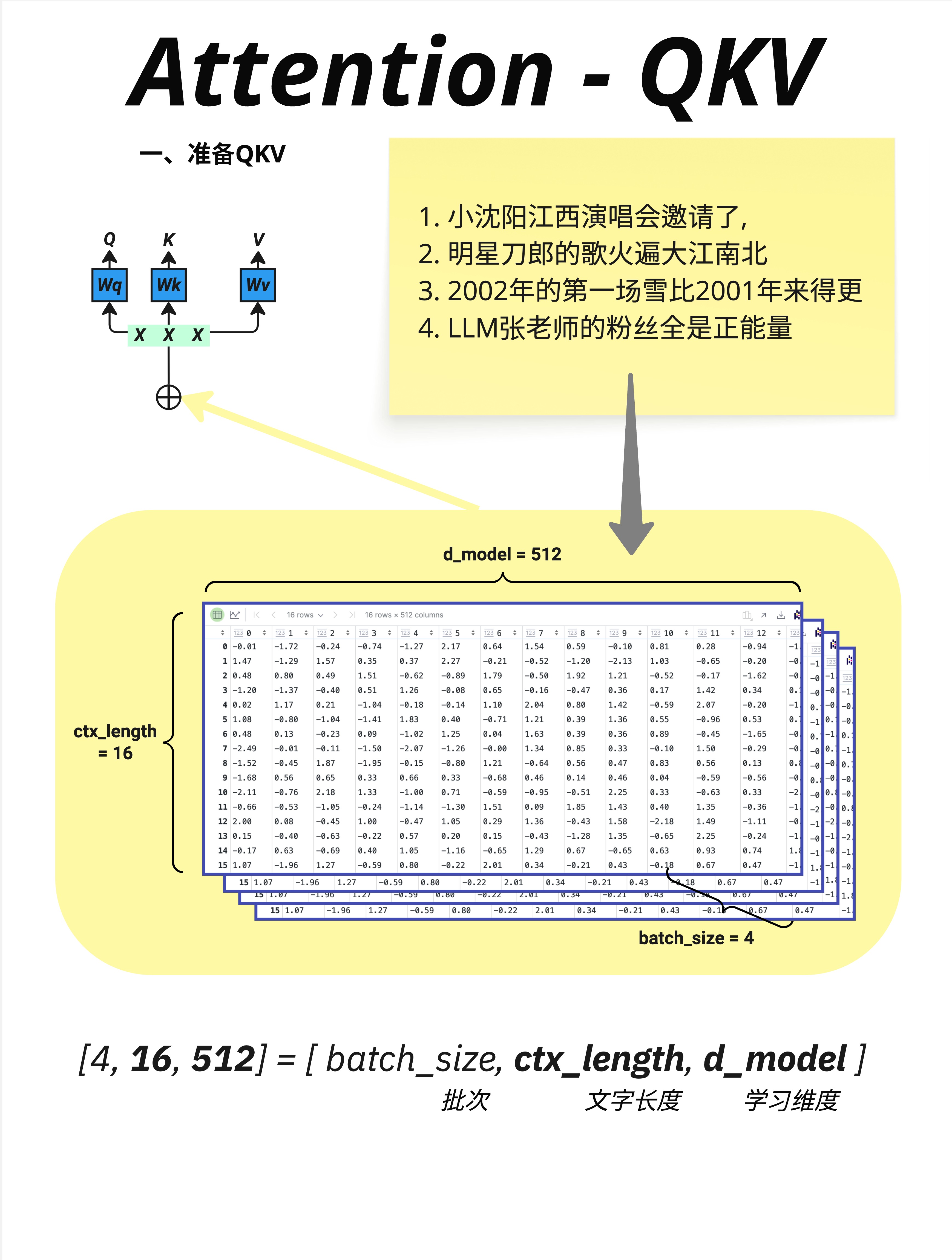
在实际训练中,我们会批量处理多个句子。输入数据的形状是:
X: [batch_size, ctx_length, d_model]以图中为例:
- batch_size = 4:同时处理 4 个句子(批次大小)
- ctx_length = 16:每个句子有 16 个 token(上下文长度)
- d_model = 512:每个 token 用 512 维向量表示(模型维度)
10.2.2 具体例子
图中展示了 4 个句子:
1. 小沈阳江西演唱会邀请了,
2. 明星刀郎的歌火遍大江南北
3. 2002年的第一场雪比2001年来得更
4. LLM张老师的粉丝全是正能量每个句子被切分成 16 个 token,每个 token 用 512 维向量表示。
所以总的输入形状是 [4, 16, 512]:
- 4 个句子
- 16 个位置
- 512 维向量
10.2.3 三个维度的含义
| 维度 | 英文 | 中文 | 含义 |
|---|---|---|---|
| batch_size | 批次 | 批次大小 | 同时处理多少个句子 |
| ctx_length | 上下文长度 | 序列长度 | 每个句子有多少个 token |
| d_model | 模型维度 | 学习维度 | 每个 token 的向量维度 |
10.3 生成 Q、K、V
10.3.1 核心思想
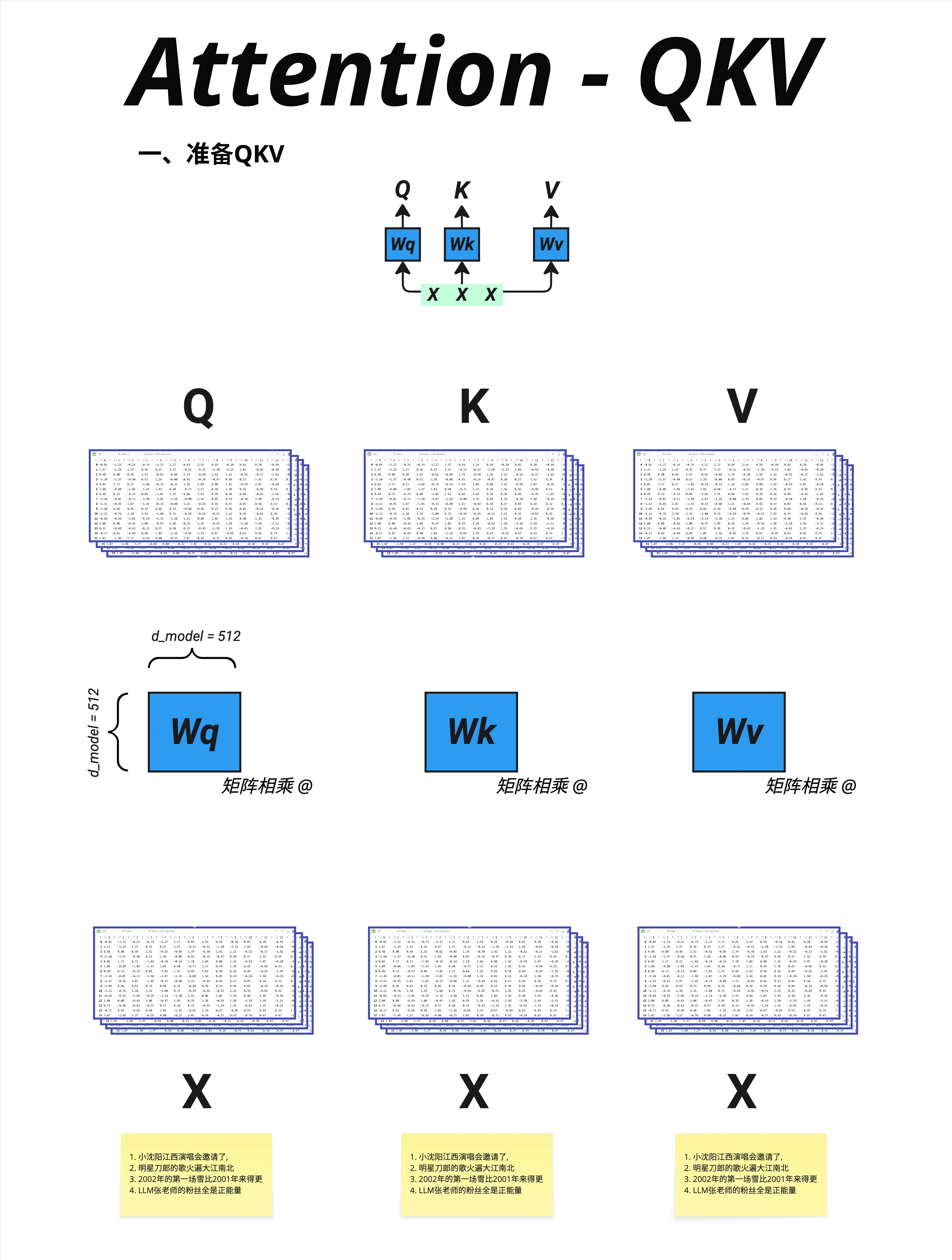
Q、K、V 都是从同一个输入 X 生成的,通过三个不同的权重矩阵:
Q = X @ Wq
K = X @ Wk
V = X @ Wv这三个权重矩阵(Wq、Wk、Wv)是可学习的参数,在训练过程中不断调整。
10.3.2 维度计算
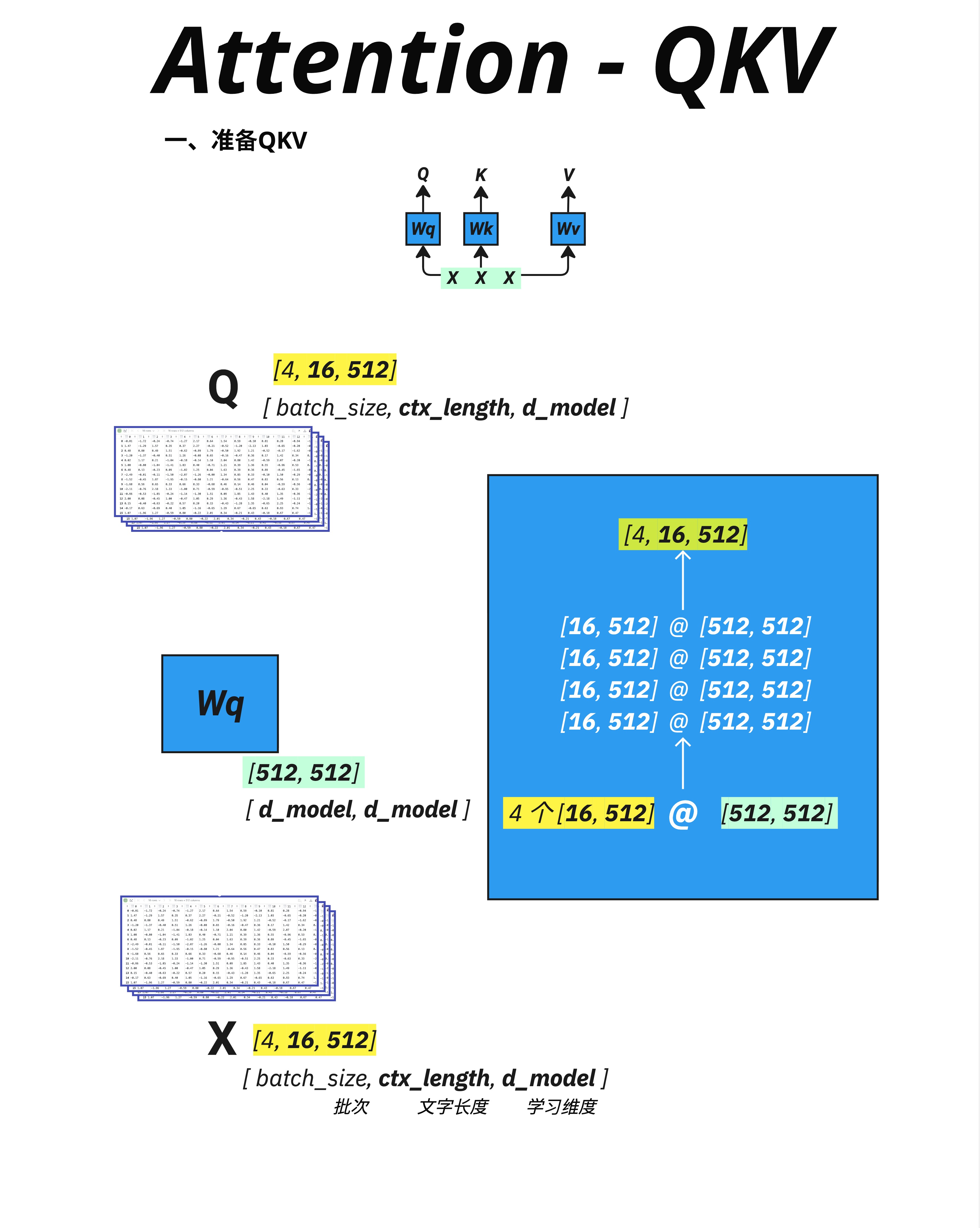
以生成 Q 为例:
X: [4, 16, 512] (batch_size, ctx_length, d_model)
Wq: [512, 512] (d_model, d_model)
Q: [4, 16, 512] (batch_size, ctx_length, d_model)矩阵乘法的维度规则:[..., A, B] @ [B, C] = [..., A, C]
所以:[4, 16, 512] @ [512, 512] = [4, 16, 512]
Q、K、V 的形状和输入 X 完全相同!
10.3.3 为什么需要三个不同的矩阵?
你可能会问:既然形状都一样,为什么要用三个不同的矩阵?
答案是:Q、K、V 承担不同的角色。
- Q(Query,查询):代表"我在找什么信息"
- K(Key,键):代表"我有什么信息可以被找到"
- V(Value,值):代表"如果被找到,我提供什么内容"
通过学习不同的 Wq、Wk、Wv,模型可以学会:
- 把同一个词转换成不同的"角色"
- 在不同的"语义空间"中进行匹配
10.3.4 一个直观的类比
想象一个图书馆检索系统:
| 角色 | 类比 | 作用 |
|---|---|---|
| Query (Q) | 读者的搜索词 | "我想找关于机器学习的书" |
| Key (K) | 每本书的索引标签 | "机器学习, Python, 入门" |
| Value (V) | 书的实际内容 | 整本书的内容 |
当你搜索时:
- 用你的 Query 和每本书的 Key 比较
- 找到匹配度高的书
- 返回这些书的 Value(内容)
10.4 第一次矩阵乘法:Q @ K^T
10.4.1 计算相似度矩阵
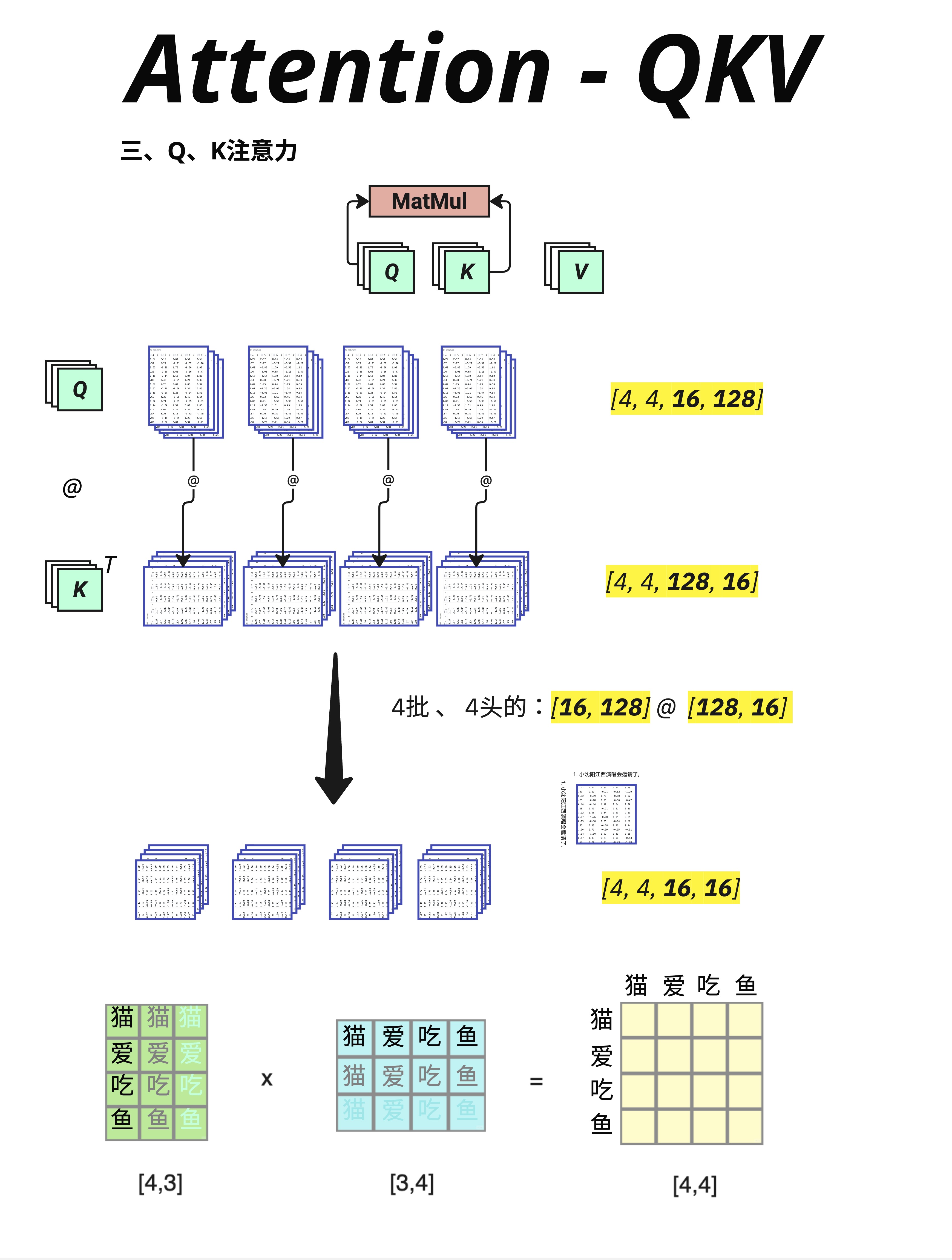
有了 Q 和 K,下一步是计算它们的相似度:
Q @ K^T注意:K 需要转置(K^T),因为我们要让 Q 的每一行和 K 的每一行做点积。
10.4.2 维度变化
Q: [4, 16, 128] (batch_size, ctx_length, d_key)
K^T: [4, 128, 16] (batch_size, d_key, ctx_length)
结果: [4, 16, 16] (batch_size, ctx_length, ctx_length)这里的 d_key = 128 是因为在 Multi-Head Attention 中,d_model 会被分成多个 head。每个 head 的维度是 d_key = d_model / num_heads = 512 / 4 = 128。这个我们下一章详细讲。
10.4.3 结果的含义
结果是一个 [4, 16, 16] 的矩阵:
- 4 个句子
- 每个句子有一个 16×16 的"注意力矩阵"
- 位置 (i, j) 表示:第 i 个 token 对第 j 个 token 的关注程度
图中下方用"猫爱吃鱼"做了一个简化示例:
猫 爱 吃 鱼
猫 [ ]
爱 [ ]
吃 [ ]
鱼 [ ]每个位置的值 = 对应 Q 行向量和 K 列向量的点积。
10.5 Scale:为什么除以 √d_key
10.5.1 缩放操作
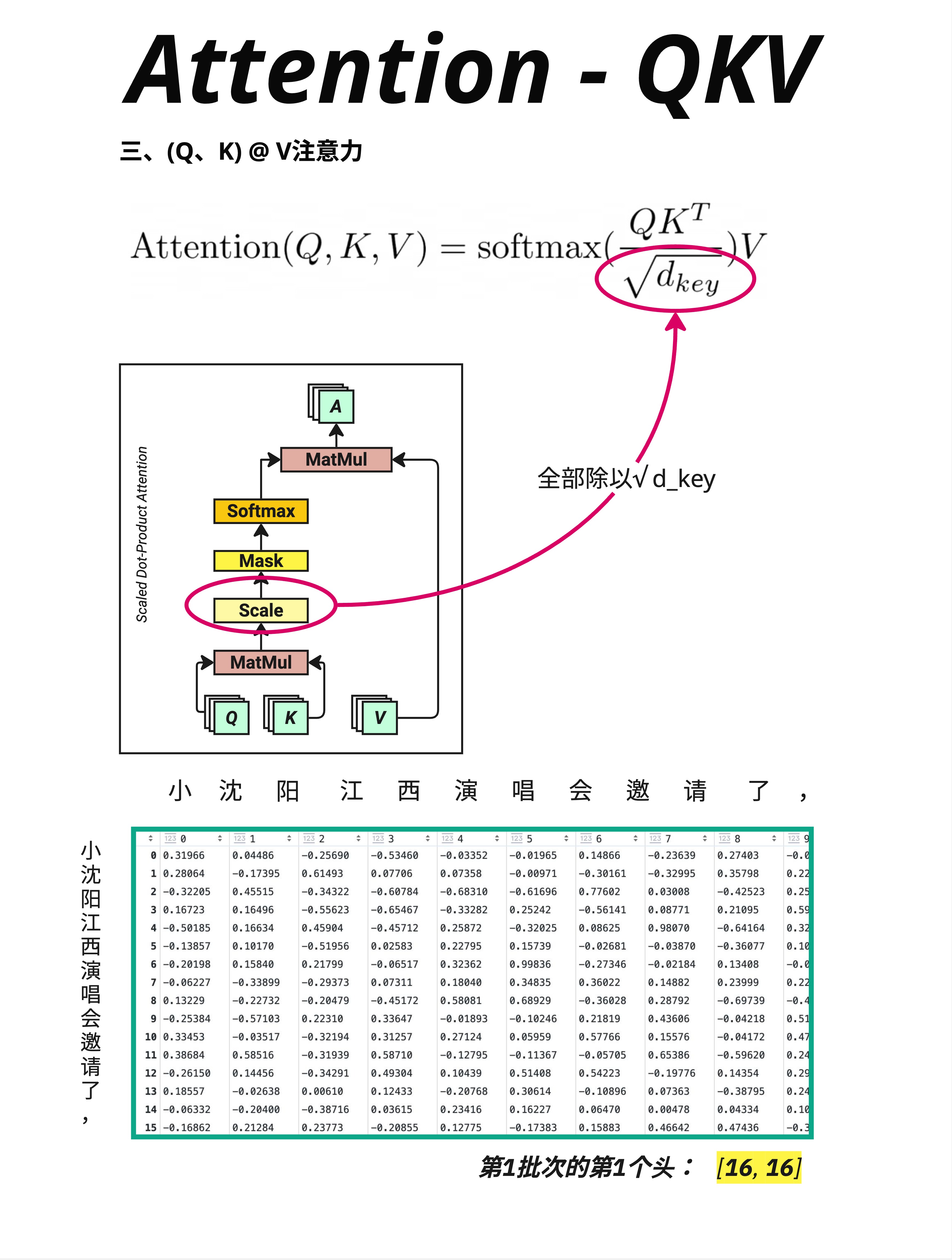
Q @ K^T 的结果需要缩放:
Attention Scores = (Q @ K^T) / √d_key图中显示的是除以 √d_key 后的结果,数值从原来的大范围(可能是几十上百)变成了更小的范围(大多在 -1 到 1 之间)。
10.5.2 为什么要缩放?
问题:当 d_key 很大时(比如 128),点积的结果会很大。
点积 = Σ(q_i × k_i) # 128 个数相乘再相加如果每个 q_i 和 k_i 的方差是 1,那么点积的方差大约是 d_key。
后果:数值太大会让 Softmax 变得极端。
Softmax([100, 1, 2]) ≈ [1.0, 0.0, 0.0] # 极端分布
Softmax([1.0, 0.1, 0.2]) ≈ [0.4, 0.3, 0.3] # 平滑分布解决方案:除以 √d_key 把数值缩放回合理范围。
点积 / √128 ≈ 点积 / 11.310.5.3 公式中的位置
这个 √d_key 就是 Scale 操作。
10.6 Mask:防止"偷看"未来
10.6.1 为什么需要 Mask?
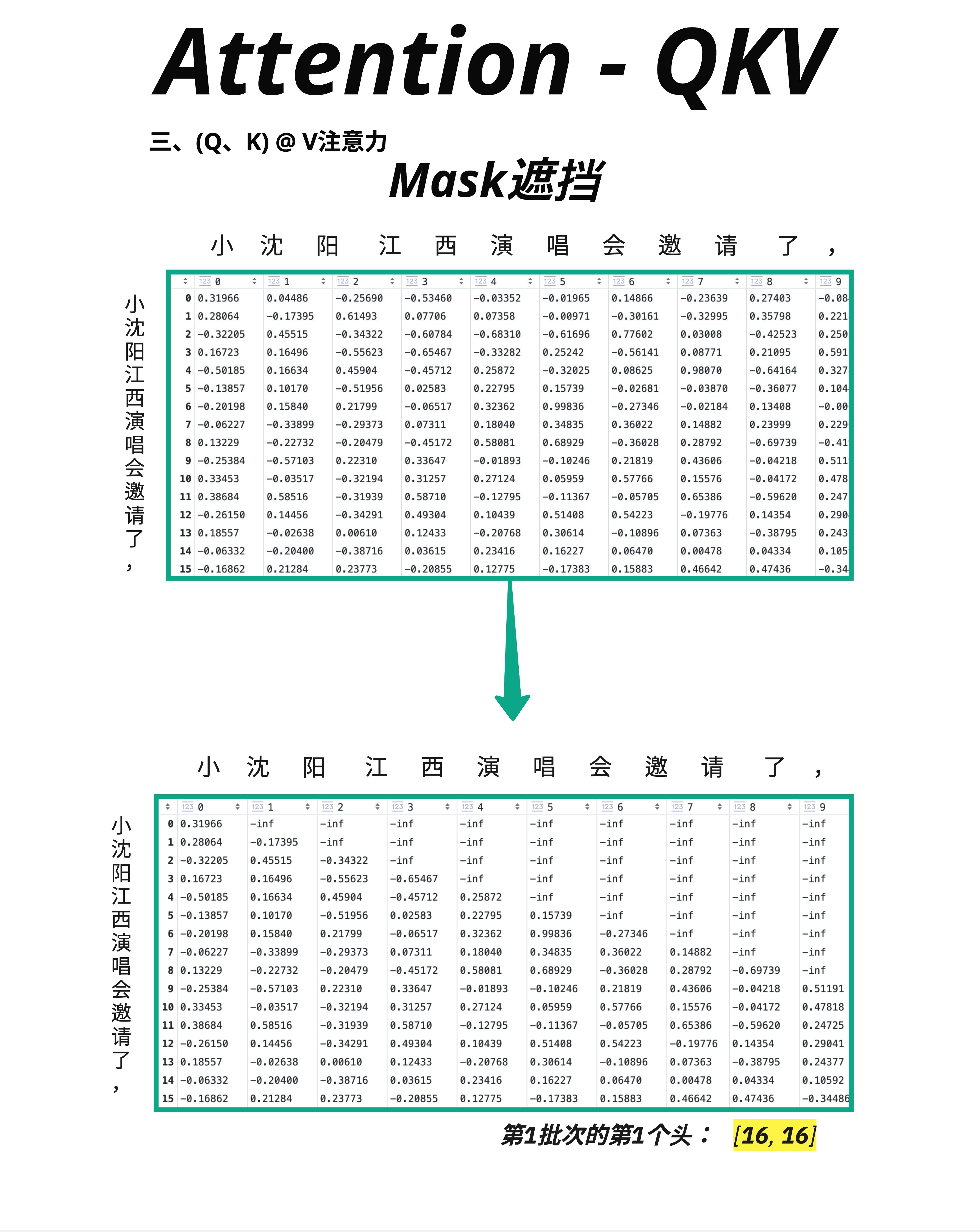
在 GPT 这样的自回归模型中,预测下一个词时不能看到未来的词。
比如预测"小沈阳江西演唱会邀请了____",模型不能看到答案。
但是 Q @ K 会计算所有位置之间的相似度,包括未来的位置!
10.6.2 Mask 的实现
解决方案:用一个三角形 Mask 把未来的位置"遮住"。
原始注意力矩阵: Mask 后:
[0.3, 0.2, 0.1, 0.4] [0.3, -∞, -∞, -∞ ]
[0.2, 0.5, 0.2, 0.1] → [0.2, 0.5, -∞, -∞ ]
[0.1, 0.3, 0.4, 0.2] [0.1, 0.3, 0.4, -∞ ]
[0.2, 0.1, 0.3, 0.4] [0.2, 0.1, 0.3, 0.4]把右上角(未来的位置)设为负无穷(-inf)。
10.6.3 为什么用 -inf?
因为 Softmax 会把 -inf 变成 0:
Softmax([0.3, -∞, -∞, -∞]) = [1.0, 0.0, 0.0, 0.0]这样,经过 Softmax 后,未来位置的注意力权重就变成 0 了——模型"看不到"未来。
10.6.4 图中的示例
图中展示了 Mask 前后的变化:
- 上方矩阵:原始的 Scale 后结果
- 下方矩阵:Mask 后结果,右上角变成了 -inf(图中可能显示为极小的数)
10.7 Softmax:变成概率分布
10.7.1 转换过程
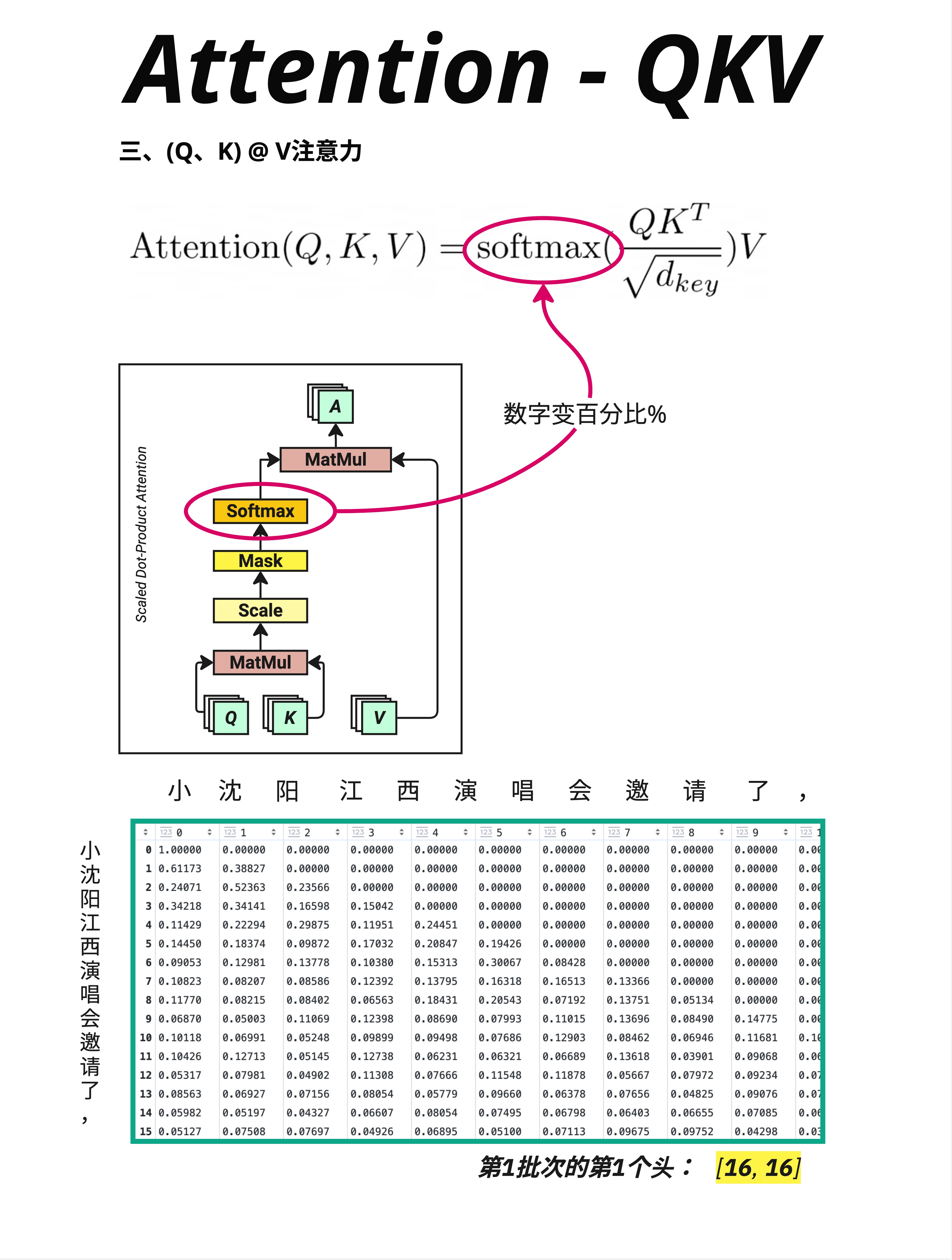
Mask 之后,对每一行应用 Softmax:
Softmax 前:[0.32, 0.04, -inf, -inf, ...]
Softmax 后:[0.52, 0.48, 0.00, 0.00, ...]10.7.2 Softmax 的作用
- 归一化:每一行的和变成 1
- 放大差异:大的值变得更大,小的值变得更小
- 处理 -inf:-inf 变成 0
10.7.3 图中的观察
看图中的数据:
- 第 0 行("小"):[1.00000, 0.00000, 0.00000, ...]
- 只能看到自己,所以自己的权重是 100%
- 第 1 行("沈"):[0.61173, 0.38827, 0.00000, ...]
- 可以看到"小"和"沈",注意力分配为 61% 和 39%
- 后面的行可以看到更多位置,注意力分布更分散
10.7.4 这就是"注意力权重"
Softmax 的输出就是注意力权重矩阵——每个位置应该分配多少注意力给其他位置。
10.8 第二次矩阵乘法:Attention @ V
10.8.1 加权求和
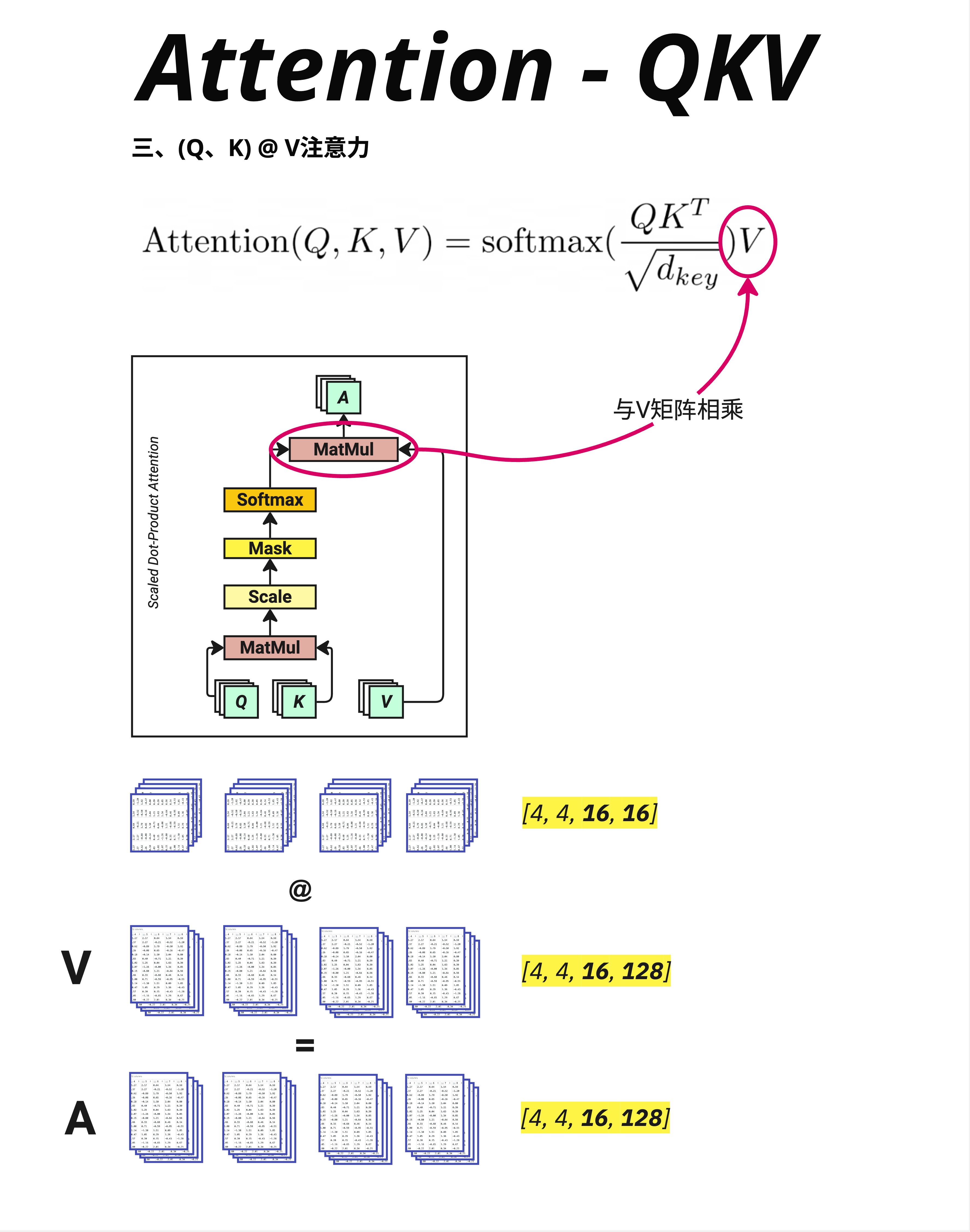
有了注意力权重,下一步是用它对 V 进行加权求和:
Output = Attention_Weights @ V10.8.2 维度变化
Attention_Weights: [4, 4, 16, 16] (batch, heads, ctx_len, ctx_len)
V: [4, 4, 16, 128] (batch, heads, ctx_len, d_key)
Output: [4, 4, 16, 128] (batch, heads, ctx_len, d_key)注意:这里显示的是 Multi-Head 的情况,有 4 个 head。
10.8.3 这一步在做什么?
每个位置的输出 = 所有位置的 V 的加权平均,权重由注意力分数决定。
output[i] = Σ(attention_weight[i,j] × V[j])如果第 i 个 token 对第 j 个 token 的注意力是 0.7,对第 k 个 token 的注意力是 0.3,那么:
output[i] = 0.7 × V[j] + 0.3 × V[k]输出是"根据注意力重新组合"的向量表示。
10.9 Attention 输出的含义
10.9.1 输出维度
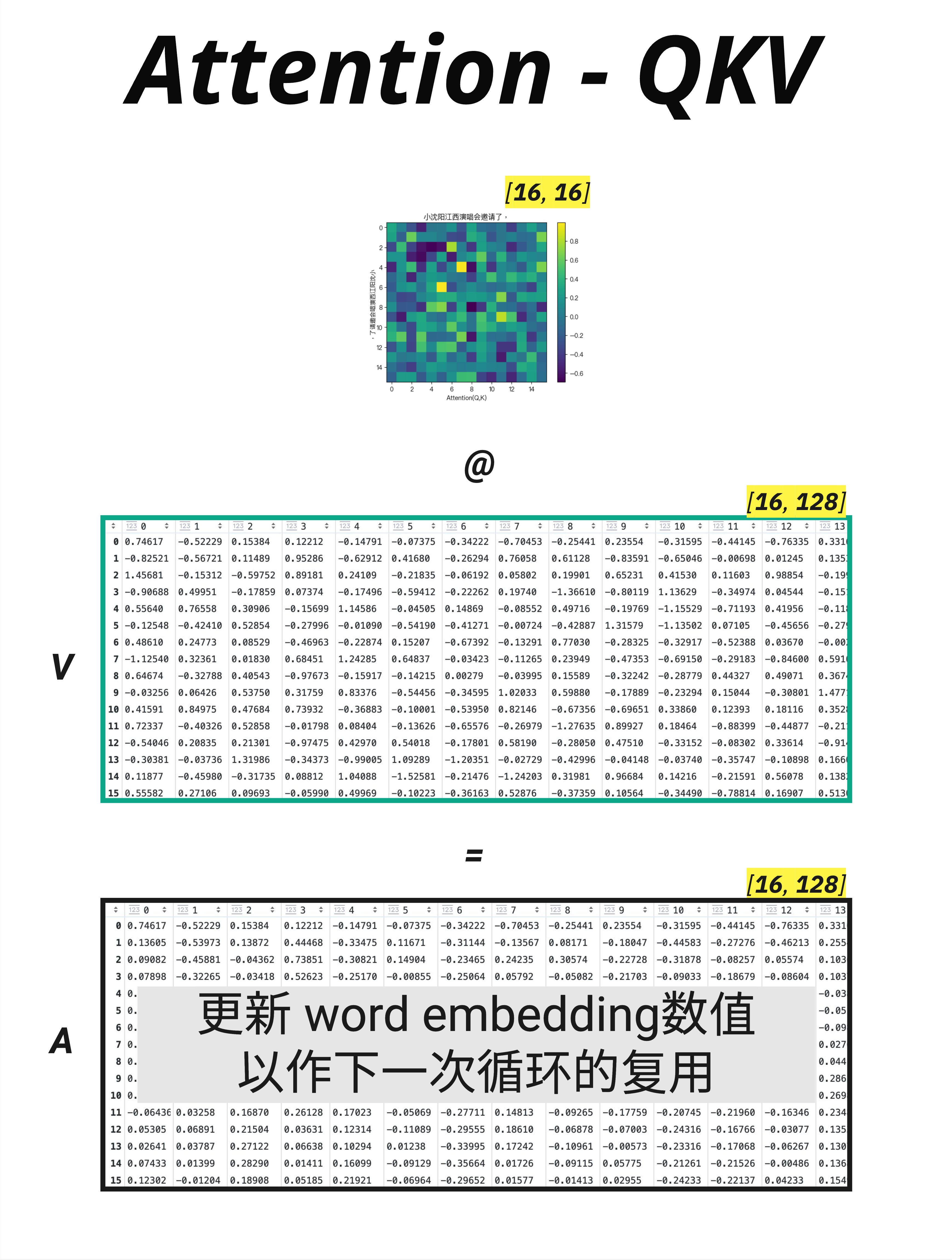
经过 Attention @ V,每个 token 得到一个新的向量表示:
输出: [batch_size, ctx_length, d_key] = [4, 16, 128](在 Multi-Head 情况下,还需要把多个 head 的输出合并,这是下一章的内容)
10.9.2 输出的语义
这个输出有什么特别之处?
它融合了上下文信息!
原始输入中,每个 token 的向量只包含自己的信息。
经过 Attention 后,每个 token 的向量变成了整个上下文的加权组合。
10.9.3 图中的说明
图中的黄色标注说得很清楚:
更新 word embedding 数值,以作下一次循环的复用
Attention 的输出会:
- 替代原来的 embedding
- 作为下一层(FFN 或下一个 Block)的输入
- 层层叠加,不断融合更多信息
10.10 完整的 Attention 计算流程
10.10.1 流程图
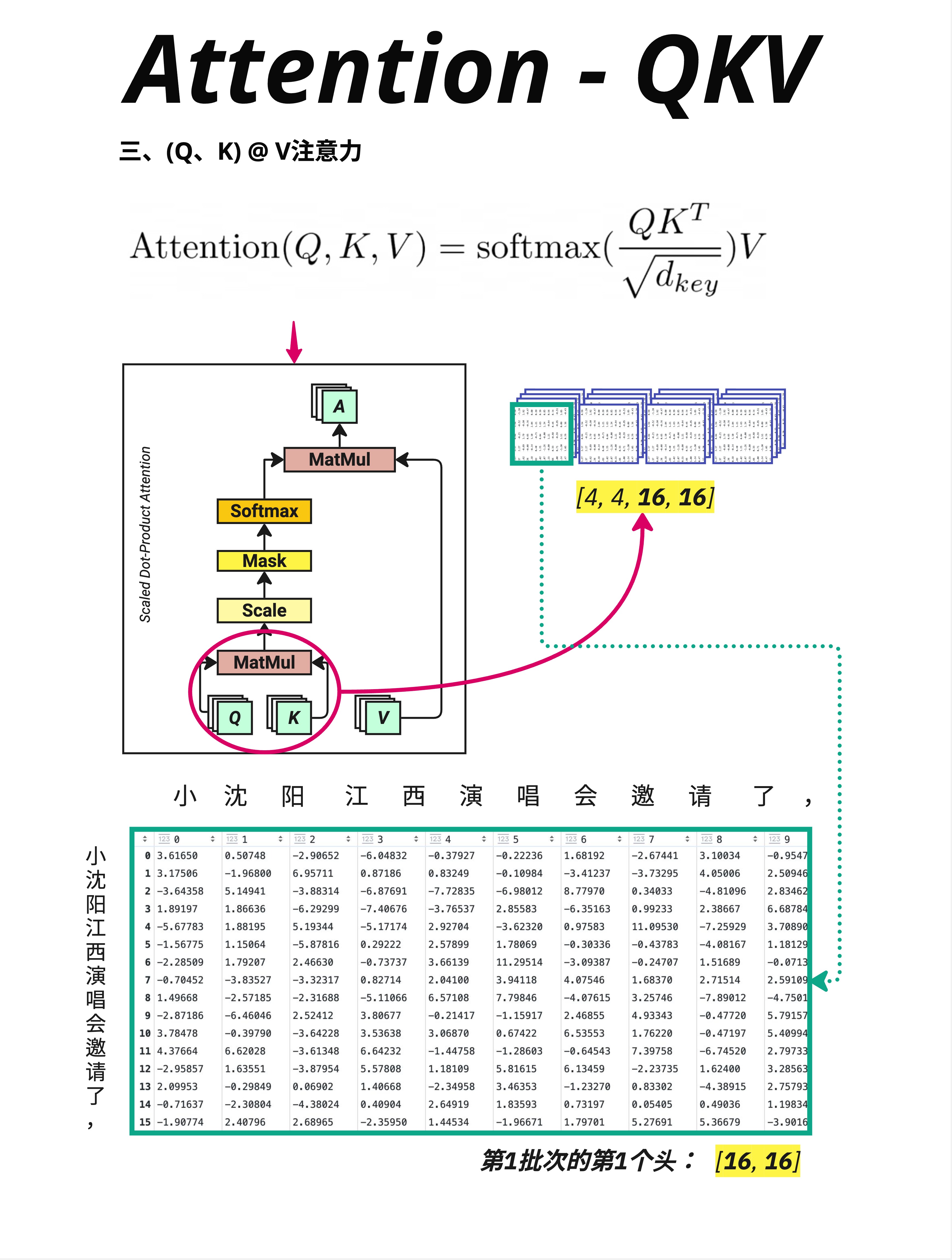
让我们把整个流程串起来:
步骤1:生成 Q, K, V
Q = X @ Wq [4, 16, 512]
K = X @ Wk [4, 16, 512]
V = X @ Wv [4, 16, 512]
↓
步骤2:计算相似度
scores = Q @ K^T [4, 16, 16]
↓
步骤3:缩放
scores = scores / √d_key [4, 16, 16]
↓
步骤4:Mask(可选,仅 Decoder)
scores[mask] = -inf [4, 16, 16]
↓
步骤5:Softmax
weights = softmax(scores) [4, 16, 16]
↓
步骤6:加权求和
output = weights @ V [4, 16, 512]10.10.2 PyTorch 代码
# 代码示例
import torch
import torch.nn.functional as F
def attention(Q, K, V, mask=None):
"""
计算 Scaled Dot-Product Attention
Args:
Q: [batch, seq_len, d_k]
K: [batch, seq_len, d_k]
V: [batch, seq_len, d_v]
mask: [batch, 1, seq_len] or [batch, seq_len, seq_len]
Returns:
output: [batch, seq_len, d_v]
attention_weights: [batch, seq_len, seq_len]
"""
d_k = Q.size(-1)
# 步骤2: Q @ K^T
scores = torch.matmul(Q, K.transpose(-2, -1))
# 步骤3: Scale
scores = scores / (d_k ** 0.5)
# 步骤4: Mask
if mask is not None:
scores = scores.masked_fill(mask == 0, float('-inf'))
# 步骤5: Softmax
attention_weights = F.softmax(scores, dim=-1)
# 步骤6: 加权求和
output = torch.matmul(attention_weights, V)
return output, attention_weights10.11 Q、K、V 的深层理解
10.11.1 三者的关系
| 角色 | 生成方式 | 作用 | 参与的计算 |
|---|---|---|---|
| Q | X @ Wq | 表示"我在找什么" | Q @ K^T |
| K | X @ Wk | 表示"我是什么"(标签) | Q @ K^T |
| V | X @ Wv | 表示"我有什么内容" | Attention @ V |
10.11.2 为什么 K 和 V 要分开?
你可能会问:K 和 V 都来自同一个输入,为什么要用两个不同的矩阵?
答案:解耦"匹配"和"提取"。
- K 负责"被匹配":决定哪些位置应该被关注
- V 负责"被提取":决定关注后提取什么信息
这给了模型更大的灵活性。
10.11.3 一个例子
考虑句子:"The cat sat on the mat"
当处理 "sat" 时:
- Q("sat") 可能在找"谁做了这个动作"
- K("cat") 的表示可能包含"我是一个主语"
- V("cat") 的表示可能包含"我是一只猫"
Q 和 K 的匹配告诉我们:sat 应该关注 cat。 V 告诉我们:关注 cat 后,获取的是"猫"的语义信息。
10.12 本章总结
10.12.1 核心概念
| 概念 | 形状 | 含义 |
|---|---|---|
| X | [batch, seq, d_model] | 输入向量 |
| Wq/Wk/Wv | [d_model, d_model] | 可学习的投影矩阵 |
| Q | [batch, seq, d_model] | 查询向量,"我在找什么" |
| K | [batch, seq, d_model] | 键向量,"我是什么" |
| V | [batch, seq, d_model] | 值向量,"我有什么内容" |
| Scores | [batch, seq, seq] | 相似度矩阵 |
| Weights | [batch, seq, seq] | 注意力权重(概率分布) |
| Output | [batch, seq, d_model] | 融合上下文后的表示 |
10.12.2 计算流程
X → [Wq, Wk, Wv] → Q, K, V
↓
Q @ K^T (相似度)
↓
/ √d_key (缩放)
↓
Mask (遮挡未来)
↓
Softmax (归一化)
↓
@ V (加权求和)
↓
Output10.12.3 核心认知
Q、K、V 是 Attention 的三个主角。Q 代表"查询",K 代表"键",V 代表"值"。通过 Q @ K 找到相关的位置,用注意力权重对 V 加权求和,得到融合了上下文信息的新表示。这就是 Attention 让模型"理解"语言的方式。
本章交付物
学完这一章,你应该能够:
- 说出 Q、K、V 各自的含义
- 解释它们是如何从输入 X 生成的
- 追踪 Attention 计算过程中的维度变化
- 理解 Mask 的作用(防止看到未来)
- 解释为什么要 Scale(除以 √d_key)
下一章预告
这一章我们学习了单头 Attention 的完整计算过程。
但实际的 Transformer 使用的是 Multi-Head Attention(多头注意力)——把 Attention 分成多个"头",每个头关注不同的信息。
为什么要这样做?多个头是怎么工作的?下一章,我们来揭开 Multi-Head Attention 的神秘面纱!