一句话总结:学习率决定了每次更新参数时"走多大一步"。太大会震荡发散,太小会收敛太慢,只有合适的学习率才能让模型稳定地学到知识。
17.1 什么是学习率?
17.1.1 参数更新的基本公式
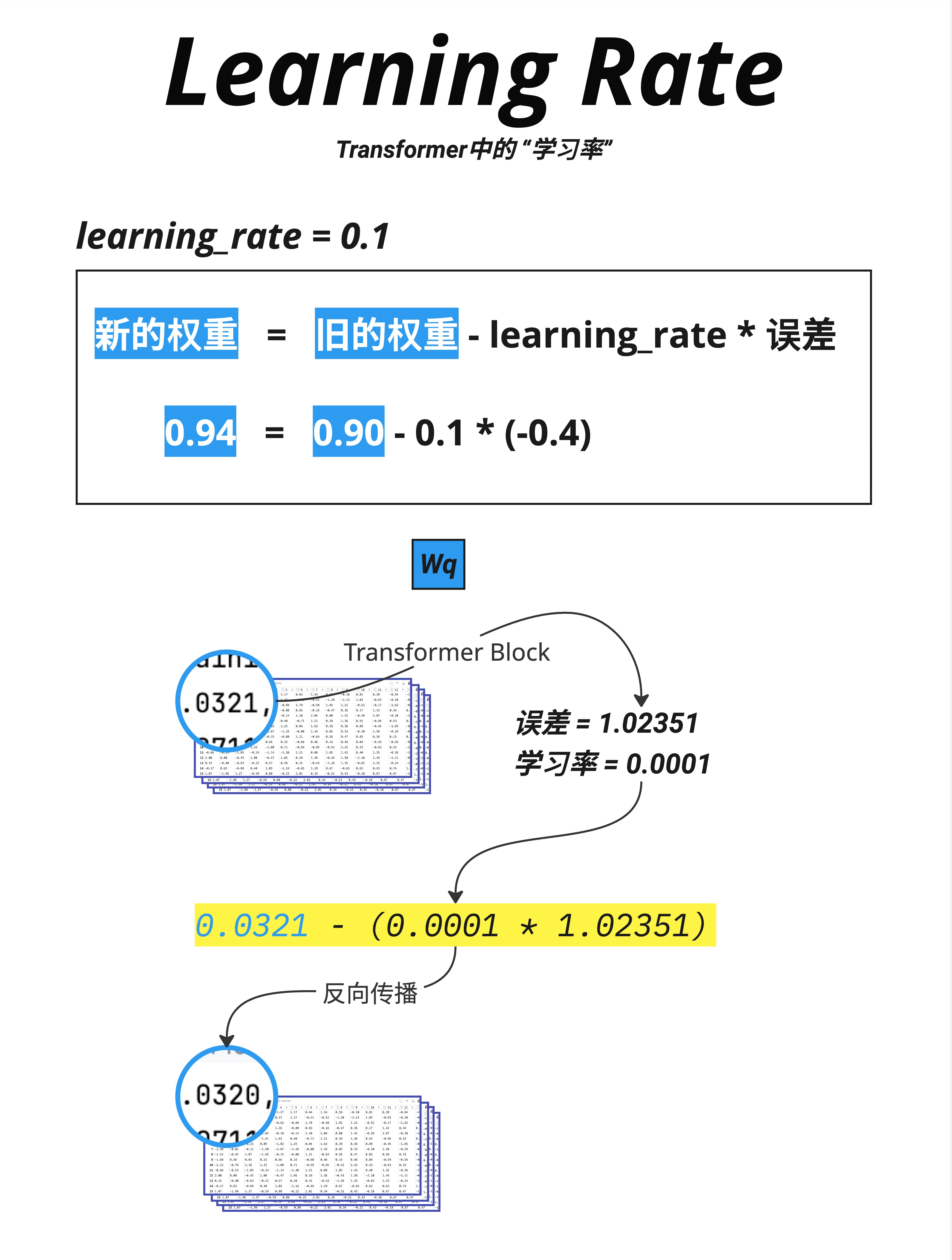
神经网络训练的核心是梯度下降:根据损失函数的梯度来更新参数。
基本公式:
新的权重 = 旧的权重 - learning_rate × 误差梯度或者用数学符号:
θ_new = θ_old - lr × ∂Loss/∂θ17.1.2 图中的具体例子
图中展示了一个简单的例子:
learning_rate = 0.1
旧权重 = 0.90
误差梯度 = -0.4
新权重 = 0.90 - 0.1 × (-0.4)
= 0.90 + 0.04
= 0.94因为梯度是负的(-0.4),说明增大这个权重可以减小损失,所以权重从 0.90 增加到 0.94。
17.1.3 学习率的作用
学习率(learning_rate,简称 lr)决定了每次更新的"步长":
- lr = 0.1:每次走梯度的 10%
- lr = 0.01:每次走梯度的 1%
- lr = 0.001:每次走梯度的 0.1%
17.2 学习率的三种情况
17.2.1 可视化理解
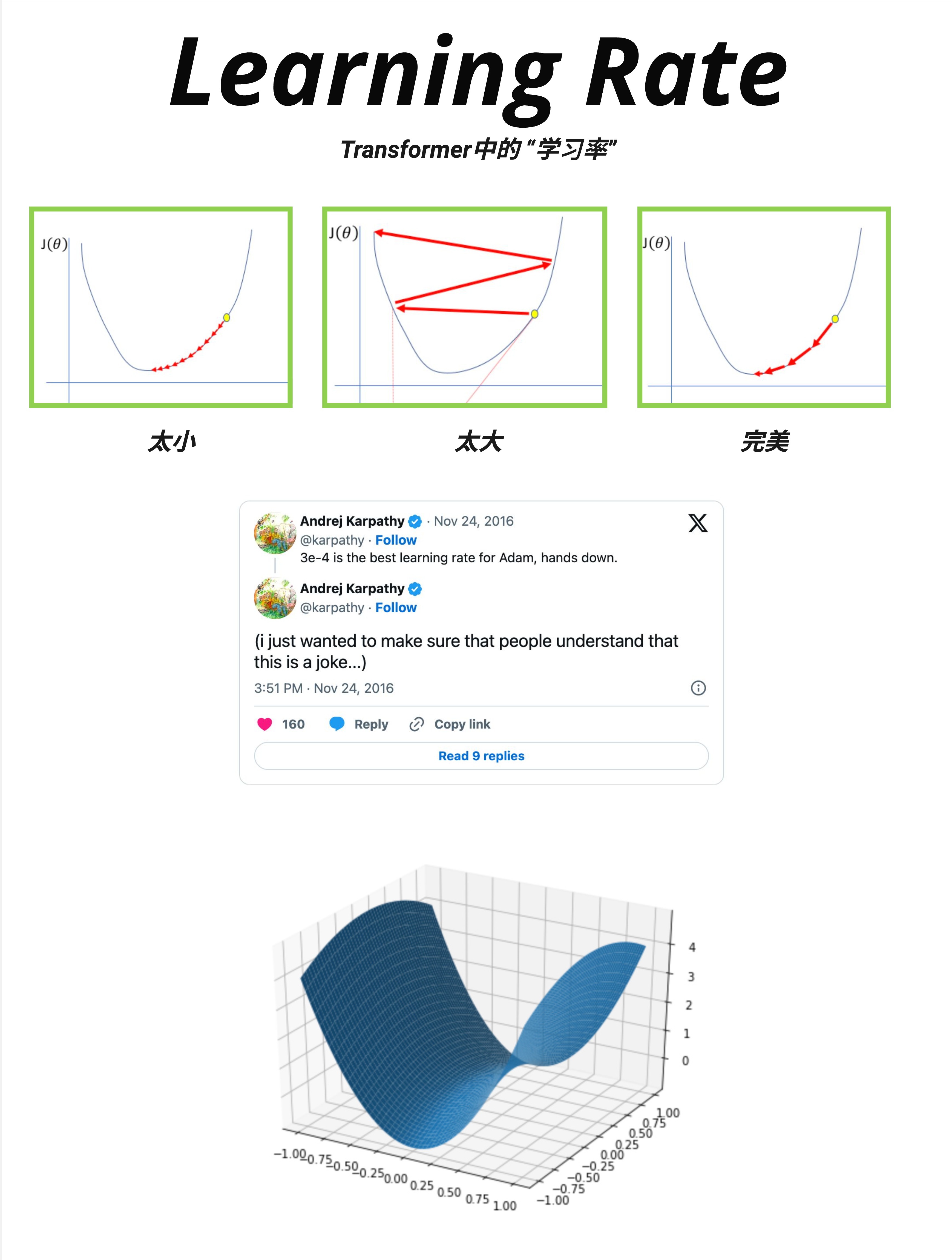
这张图展示了三种学习率的效果:
太小(左图):
- 每一步都很小
- 需要很多步才能到达最低点
- 训练时间很长
- 可能卡在局部最优
太大(中图):
- 每一步都很大
- 会在最低点附近来回震荡
- 可能跳过最低点
- 甚至可能发散(越来越差)
完美(右图):
- 步长适中
- 稳定地下降到最低点
- 收敛快且稳定
17.2.2 Andrej Karpathy 的玩笑
图中还引用了 Andrej Karpathy 的推特:
"3e-4 is the best learning rate for Adam, hands down."
"(i just wanted to make sure that people understand that this is a joke...)"
这个"玩笑"反映了一个有趣的现实:3×10⁻⁴ (0.0003) 确实是一个常用的起始学习率,在很多情况下效果不错。
但当然,最佳学习率取决于具体任务、模型大小、批次大小等因素。
17.2.3 损失景观(Loss Landscape)
图中下方展示了一个 3D 的损失景观:
- X、Y 轴:两个参数的值
- Z 轴:损失值
这个曲面有山有谷,训练的目标是找到最低点(全局最优)。
学习率决定了我们在这个曲面上"走"的速度。
17.3 哪些参数会被更新?
17.3.1 Transformer 中的可学习参数
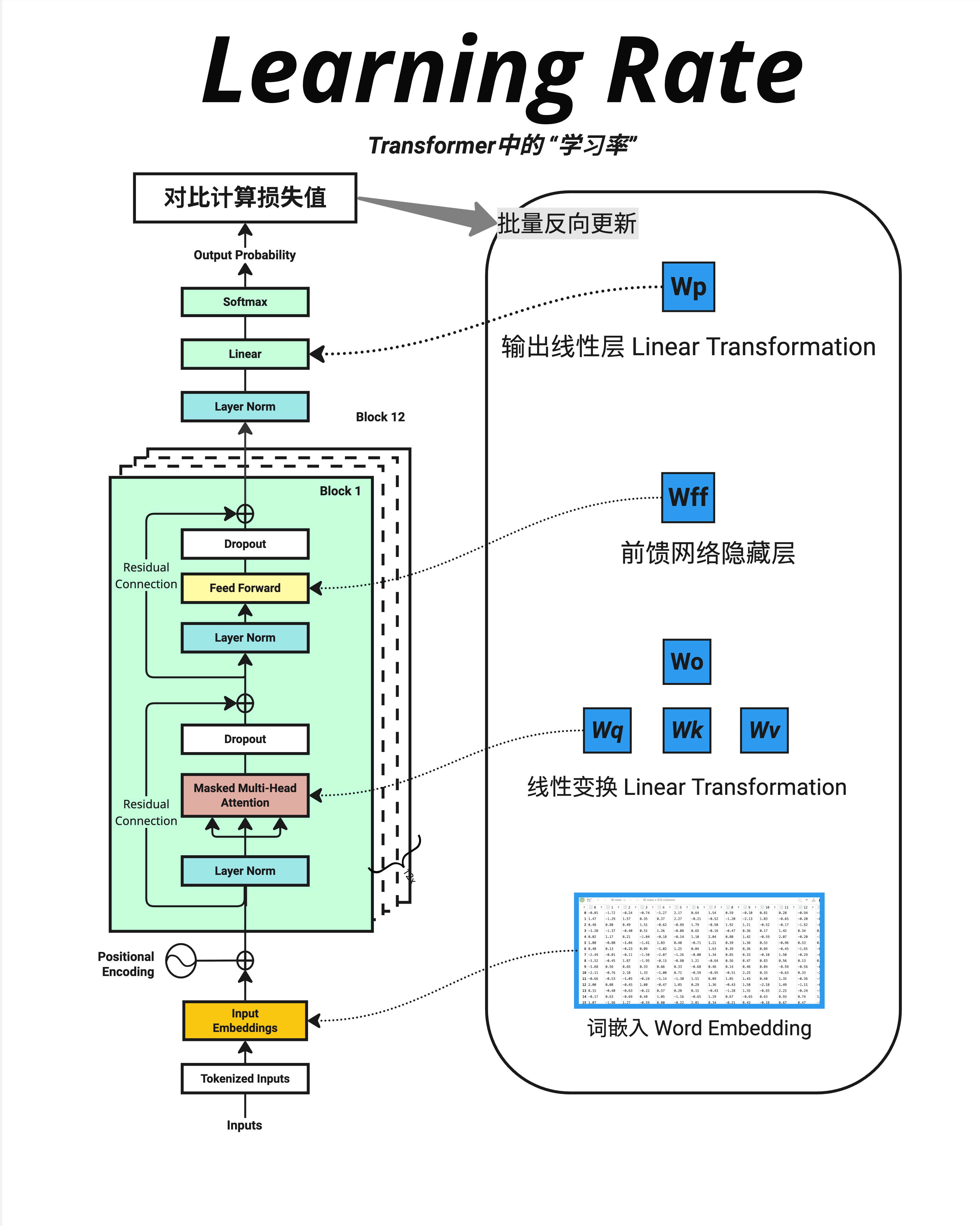
这张图展示了 Transformer 中所有可学习参数的位置:
1. 词嵌入 Word Embedding
- 每个词的向量表示
- 参数量:
vocab_size × d_model
2. Attention 层的权重
- Wq、Wk、Wv:生成 Q、K、V 的矩阵
- Wo:输出投影矩阵
- 每层参数量:
4 × d_model²
3. FFN 层的权重
- Wff:前馈网络的权重
- 每层参数量:
2 × d_model × d_ff
4. 输出线性层 Wp
- 映射到词表
- 参数量:
d_model × vocab_size
17.3.2 批量反向更新
图中标注了"批量反向更新"的流程:
计算损失值(对比预测和真实)
↓
反向传播
↓
计算每个参数的梯度
↓
批量更新所有参数所有参数在同一时间被更新,使用各自的梯度和相同的学习率。
17.4 PyTorch 实现
17.4.1 代码示例
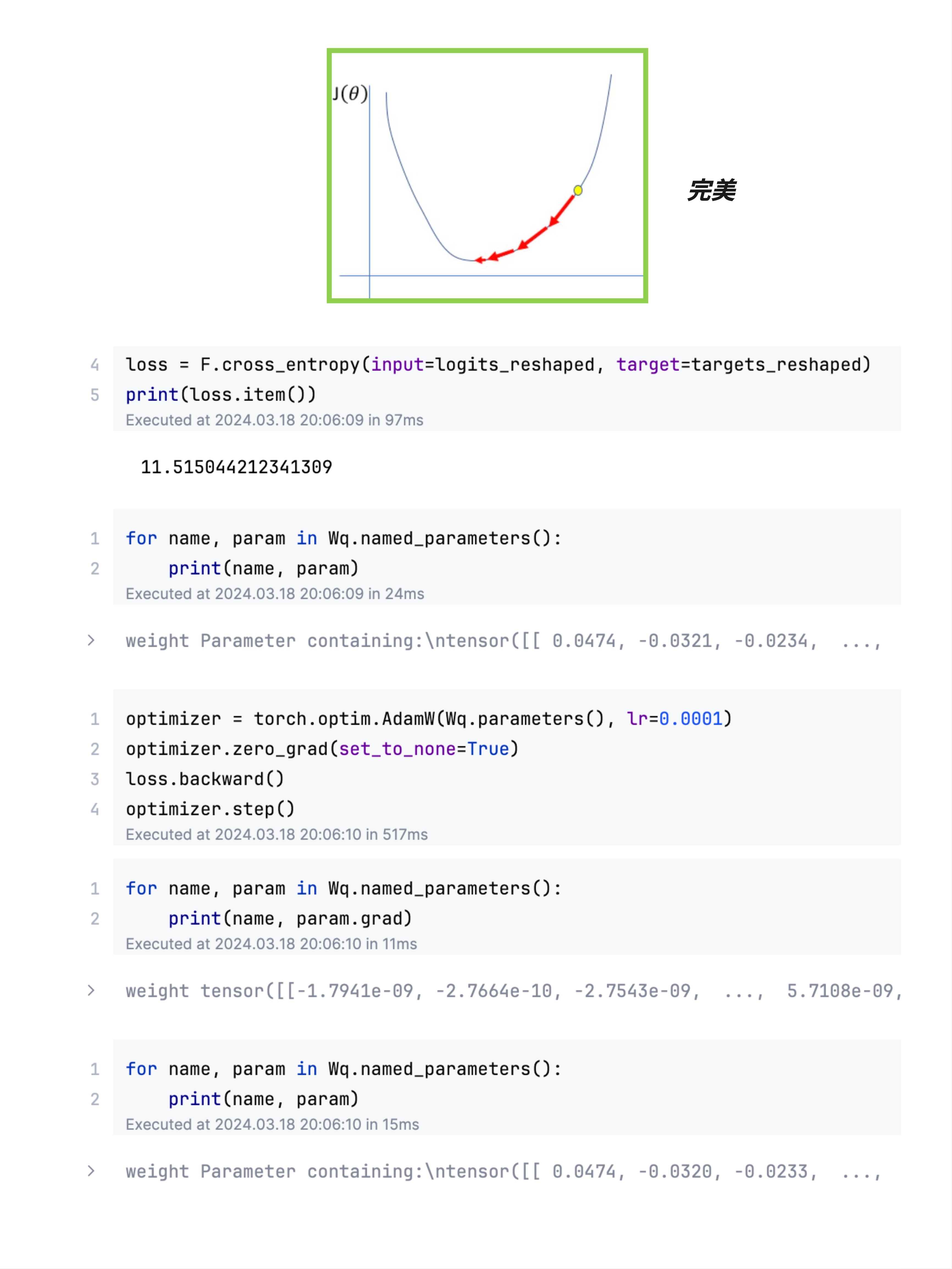
这张图展示了 PyTorch 中的训练代码:
# 代码示例
import torch
import torch.nn.functional as F
# 1. 计算损失
loss = F.cross_entropy(input=logits_reshaped, target=targets_reshaped)
print(loss.item()) # 输出:11.515044212341309
# 2. 查看更新前的参数
for name, param in Wq.named_parameters():
print(name, param)
# weight Parameter containing:
# tensor([[ 0.0474, -0.0321, -0.0234, ...
# 3. 创建优化器并执行一步更新
optimizer = torch.optim.AdamW(Wq.parameters(), lr=0.0001)
optimizer.zero_grad() # 清空之前的梯度
loss.backward() # 计算梯度
optimizer.step() # 更新参数
# 4. 查看梯度
for name, param in Wq.named_parameters():
print(name, param.grad)
# weight tensor([[-1.7941e-09, -2.7664e-10, -2.7543e-09, ...
# 5. 查看更新后的参数
for name, param in Wq.named_parameters():
print(name, param)
# weight Parameter containing:
# tensor([[ 0.0474, -0.0320, -0.0233, ...17.4.2 关键步骤解释
loss.backward():计算所有参数的梯度optimizer.zero_grad():清空梯度(否则会累加)optimizer.step():根据梯度和学习率更新参数
17.4.3 参数变化观察
图中可以看到参数的微小变化:
更新前:0.0474, -0.0321, -0.0234, ...
更新后:0.0474, -0.0320, -0.0233, ...变化非常微小(第四位小数),因为:
- 学习率很小(0.0001)
- 梯度也很小(~10⁻⁹)
但经过成千上万次更新,这些微小的变化会累积成显著的学习效果。
17.5 常用的优化器
17.5.1 SGD(随机梯度下降)
最基本的优化器:
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)更新公式:
θ = θ - lr × gradient17.5.2 Adam
最常用的优化器,自适应调整每个参数的学习率:
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)特点:
- 维护梯度的一阶矩(均值)和二阶矩(方差)
- 自动为每个参数调整学习率
- 对稀疏梯度效果好
17.5.3 AdamW
Adam 的改进版,修复了权重衰减的问题:
optimizer = torch.optim.AdamW(model.parameters(), lr=0.0001, weight_decay=0.01)大模型训练的首选优化器。
17.5.4 常见配置
| 模型 | 优化器 | 初始学习率 | Weight Decay |
|---|---|---|---|
| GPT-2 | Adam | 2.5e-4 | 0.01 |
| GPT-3 | Adam | 6e-5 ~ 2e-4 | 0.1 |
| LLaMA | AdamW | 3e-4 | 0.1 |
17.6 学习率调度
17.6.1 为什么需要调度?
一个固定的学习率往往不是最优的:
- 训练初期:需要较大的学习率快速下降
- 训练后期:需要较小的学习率精细调整
17.6.2 常见的调度策略
Warmup + Cosine Decay(最常用):
学习率
↑
| /\
| / \__
| / \___
| / \____
+------------------------→ 训练步数
↑ ↑
warmup cosine decay- Warmup 阶段:学习率从很小逐渐增加到目标值
- Decay 阶段:学习率按余弦函数逐渐减小
17.6.3 PyTorch 实现
# 代码示例
from torch.optim.lr_scheduler import CosineAnnealingLR, LinearLR, SequentialLR
# 基础优化器
optimizer = torch.optim.AdamW(model.parameters(), lr=3e-4)
# Warmup:前 1000 步线性增加
warmup_scheduler = LinearLR(
optimizer,
start_factor=0.1, # 从 lr×0.1 开始
total_iters=1000
)
# Cosine decay:之后余弦衰减
cosine_scheduler = CosineAnnealingLR(
optimizer,
T_max=100000, # 总步数
eta_min=1e-5 # 最小学习率
)
# 组合
scheduler = SequentialLR(
optimizer,
schedulers=[warmup_scheduler, cosine_scheduler],
milestones=[1000]
)
# 训练循环中
for step in range(total_steps):
loss = train_step(...)
optimizer.step()
scheduler.step() # 更新学习率17.6.4 为什么要 Warmup?
训练初期:
- 参数是随机初始化的
- 梯度方向可能不准确
- 大学习率容易导致不稳定
Warmup 让模型先"热身":
- 从小学习率开始
- 逐渐增加到目标值
- 给模型时间找到正确的方向
17.7 学习率与其他超参数的关系
17.7.1 批次大小(Batch Size)
更大的批次 → 可以用更大的学习率
经验法则(Linear Scaling Rule):
如果批次大小翻倍,学习率也可以翻倍原因:更大的批次意味着梯度估计更准确,可以走更大的步。
17.7.2 模型大小
更大的模型 → 通常需要更小的学习率
| 模型规模 | 参数量 | 典型学习率 |
|---|---|---|
| Small | ~100M | 3e-4 ~ 1e-3 |
| Medium | ~1B | 1e-4 ~ 3e-4 |
| Large | ~10B | 3e-5 ~ 1e-4 |
| XL | ~100B+ | 1e-5 ~ 3e-5 |
17.7.3 Weight Decay
Weight Decay(权重衰减)是一种正则化技术:
θ = θ - lr × (gradient + weight_decay × θ)它倾向于让权重变小,防止过拟合。
常见值:0.01 ~ 0.1
17.8 实践建议
17.8.1 如何选择学习率?
-
从常用值开始:
- Adam/AdamW:3e-4 是个好起点
- 大模型:1e-4 或更小
-
观察训练曲线:
- 损失平稳下降 → 学习率合适
- 损失震荡 → 学习率太大
- 损失下降太慢 → 学习率太小
-
使用学习率查找器:
- 从很小的学习率开始
- 逐渐增大,观察损失
- 选择损失下降最快的区域
17.8.2 常见问题诊断
| 现象 | 可能原因 | 解决方案 |
|---|---|---|
| 损失不下降 | 学习率太小 | 增大学习率 |
| 损失剧烈震荡 | 学习率太大 | 减小学习率 |
| 损失突然变 NaN | 学习率过大 / 数值溢出 | 减小学习率,检查数据 |
| 损失下降后又上升 | 过拟合 / 学习率未衰减 | 加入衰减,增加正则化 |
17.8.3 我的推荐配置
# 推荐的训练配置
optimizer = torch.optim.AdamW(
model.parameters(),
lr=3e-4, # 初始学习率
betas=(0.9, 0.95), # Adam 的动量参数
weight_decay=0.1 # 权重衰减
)
# Warmup + Cosine Decay
total_steps = 100000
warmup_steps = 2000
scheduler = get_cosine_schedule_with_warmup(
optimizer,
num_warmup_steps=warmup_steps,
num_training_steps=total_steps
)17.9 本章总结
17.9.1 核心公式
新权重 = 旧权重 - 学习率 × 梯度
θ_new = θ_old - lr × ∂Loss/∂θ17.9.2 学习率的影响
| 学习率 | 效果 |
|---|---|
| 太大 | 震荡、发散 |
| 太小 | 收敛慢、卡住 |
| 合适 | 稳定收敛 |
17.9.3 常用配置
| 组件 | 推荐值 |
|---|---|
| 优化器 | AdamW |
| 初始学习率 | 1e-4 ~ 3e-4 |
| Weight Decay | 0.01 ~ 0.1 |
| 调度 | Warmup + Cosine Decay |
| Warmup 步数 | 总步数的 1-5% |
17.9.4 核心认知
学习率是训练神经网络最重要的超参数之一。它决定了每次更新的步长:太大会震荡发散,太小会收敛太慢。配合 Warmup 和 Cosine Decay 等调度策略,可以让训练更加稳定高效。对于大模型,常用 AdamW 优化器,配合 3e-4 左右的学习率和 0.1 左右的 weight decay。
本章交付物
学完这一章,你应该能够:
- 解释学习率在参数更新中的作用
- 理解学习率太大/太小的影响
- 知道常用的优化器(SGD、Adam、AdamW)
- 了解学习率调度的必要性(Warmup + Decay)
Part 4 总结
恭喜你完成了 Part 4:完整架构!
让我们回顾这五章学到的内容:
| 章节 | 主题 | 核心内容 |
|---|---|---|
| 第 13 章 | 残差连接与 Dropout | 梯度直通、防过拟合 |
| 第 14 章 | 词嵌入+位置信息 | 相加而非拼接的设计 |
| 第 15 章 | 完整前向传播 | 从输入到输出的完整流程 |
| 第 16 章 | 训练 vs 推理 | 并行训练、串行推理 |
| 第 17 章 | 学习率 | 步长控制与调度策略 |
现在你已经理解了 Transformer 的完整工作原理!从输入的文字,到最终输出的预测,每一步都清清楚楚。
下一章预告
Part 5 将进入代码实现阶段:
- 第 18 章:手写 Model.py - 模型定义
- 第 19 章:手写 Train.py - 训练循环
- 第 20 章:手写 Inference.py - 推理逻辑
我们将从零开始,一行一行地实现一个完整的 GPT 模型!