English中文日本語

当序列长度从千级跃升到百万级，O(n^2) 的 Full Attention 成为不可逾越的瓶颈。Sparse Attention 通过"选择性关注"降低复杂度，而 Infini Attention 则用压缩记忆实现理论上无限的上下文窗口。

24.1 Full Attention 的瓶颈：为什么 n^2 是致命的？

24.1.1 从数字看问题

让我们先直观感受一下 Full Attention 的计算量。标准的 Self-Attention 需要计算一个 N x N 的注意力矩阵，其中 N 是序列长度：

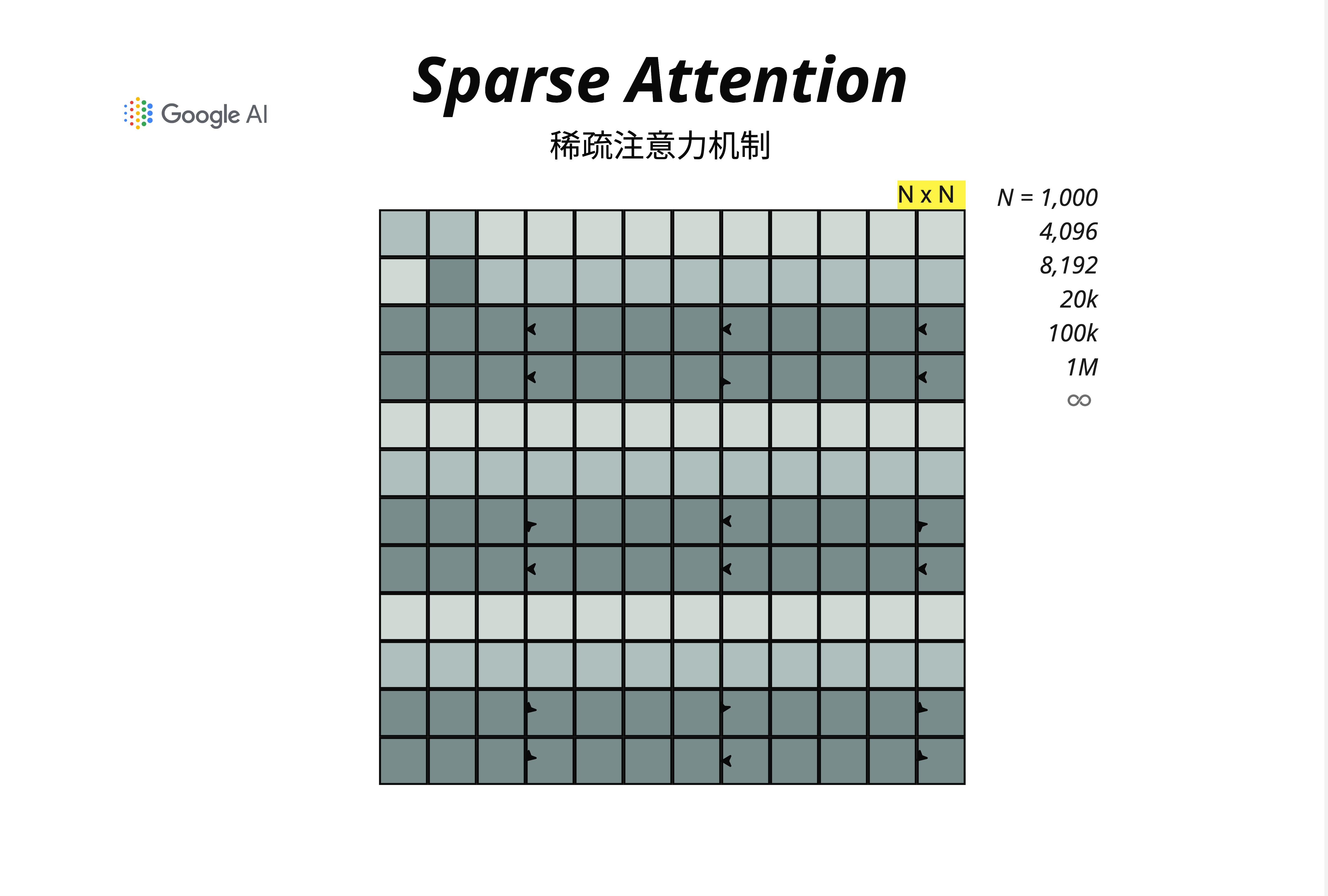
Sparse Attention 介绍

看看这些数字：

  • N = 1,000 时：需要计算 1,000,000 个注意力分数
  • N = 4,096 时：需要计算约 1,600 万个注意力分数
  • N = 8,192 时：需要计算约 6,700 万个注意力分数
  • N = 100,000 时：需要计算 100 亿个注意力分数
  • N = 1,000,000 时：需要计算 1 万亿个注意力分数

这就是 O(n^2) 的可怕之处：当序列长度增加 10 倍，计算量增加 100 倍。

24.1.2 内存才是真正的杀手

计算量还不是最致命的问题。真正的瓶颈在于显存。

在 Attention 计算中，我们需要存储完整的 N x N 注意力矩阵。假设使用 FP16（每个数占 2 字节）：

序列长度注意力矩阵大小单层显存占用
4,0964096 x 409632 MB
8,1928192 x 8192128 MB
32,76832768 x 327682 GB
131,072131072 x 13107232 GB

一个 32 层的模型，光注意力矩阵就可能吃掉整块 GPU 的显存！

24.1.3 现实需求 vs 技术瓶颈

但现实世界的需求却在不断推动上下文窗口的扩展：

  • 长文档理解：一本书可能有 50 万字，约 100 万 tokens
  • 代码分析：一个完整的代码仓库可能有数万行代码
  • 多轮对话：长时间的对话历史需要被记住
  • 视频理解：一小时视频可能产生数十万个 token

这就引出了本章的核心问题：如何在不牺牲太多性能的前提下，突破 O(n^2) 的限制？

24.2 Sparse Attention：不是所有 token 都值得关注

24.2.1 核心直觉

想象你在阅读一本小说。当你读到第 500 页的某个句子时，你真的需要同时关注第 1 页到第 499 页的每一个词吗？

显然不需要。你可能只需要关注：

  1. 最近读过的内容（局部上下文）
  2. 章节开头的关键句（全局锚点）
  3. 之前提到的重要人物和地点（关键信息）

Sparse Attention 的核心思想就是：让每个 token 只关注"真正重要"的其他 token，而不是所有 token。

24.2.2 从 Full Attention 到 Sparse Attention

Full Attention 就像一个完全连接的图——每个节点都与其他所有节点相连：

BigBird 稀疏模式

图中上方展示了 Full Attention：一个 N x N 的稠密矩阵，对应一个全连接图。每个词（如 "The", "firm", "for", "York" 等）都与其他所有词有连接。

而 Sparse Attention 则是一个稀疏连接的图——只保留"重要"的连接，大大减少计算量。

24.2.3 三种基本稀疏模式

Sparse Attention 的关键在于如何选择"重要"的连接。业界发展出三种主要的稀疏模式：

1. Random Attention（随机注意力）

随机选择一些 token 进行关注。虽然看起来很粗暴，但理论上可以保证信息在图中的传播。

2. Window/Sliding Window Attention（滑动窗口注意力）

每个 token 只关注其周围固定窗口内的 token。这基于一个假设：局部上下文通常最重要。

3. Global Attention（全局注意力）

指定某些特殊 token（如 [CLS] 或句首词）与所有其他 token 相连。这些"枢纽"token 负责收集和分发全局信息。

24.3 Longformer 与 BigBird：稀疏模式的组合艺术

24.3.1 构建稀疏注意力矩阵

让我们逐步看看如何构建一个有效的 Sparse Attention 矩阵：

稀疏注意力机制构建步骤

第 1 步：Random Tokens

首先，随机选择一些位置进行关注（图中黄色格子）。这保证了即使相距很远的 token 也有机会直接交换信息。

第 2 步：Window Tokens

在随机注意力的基础上，添加滑动窗口。每个 token 都关注其左右邻居（图中对角线附近的黄色区域）。

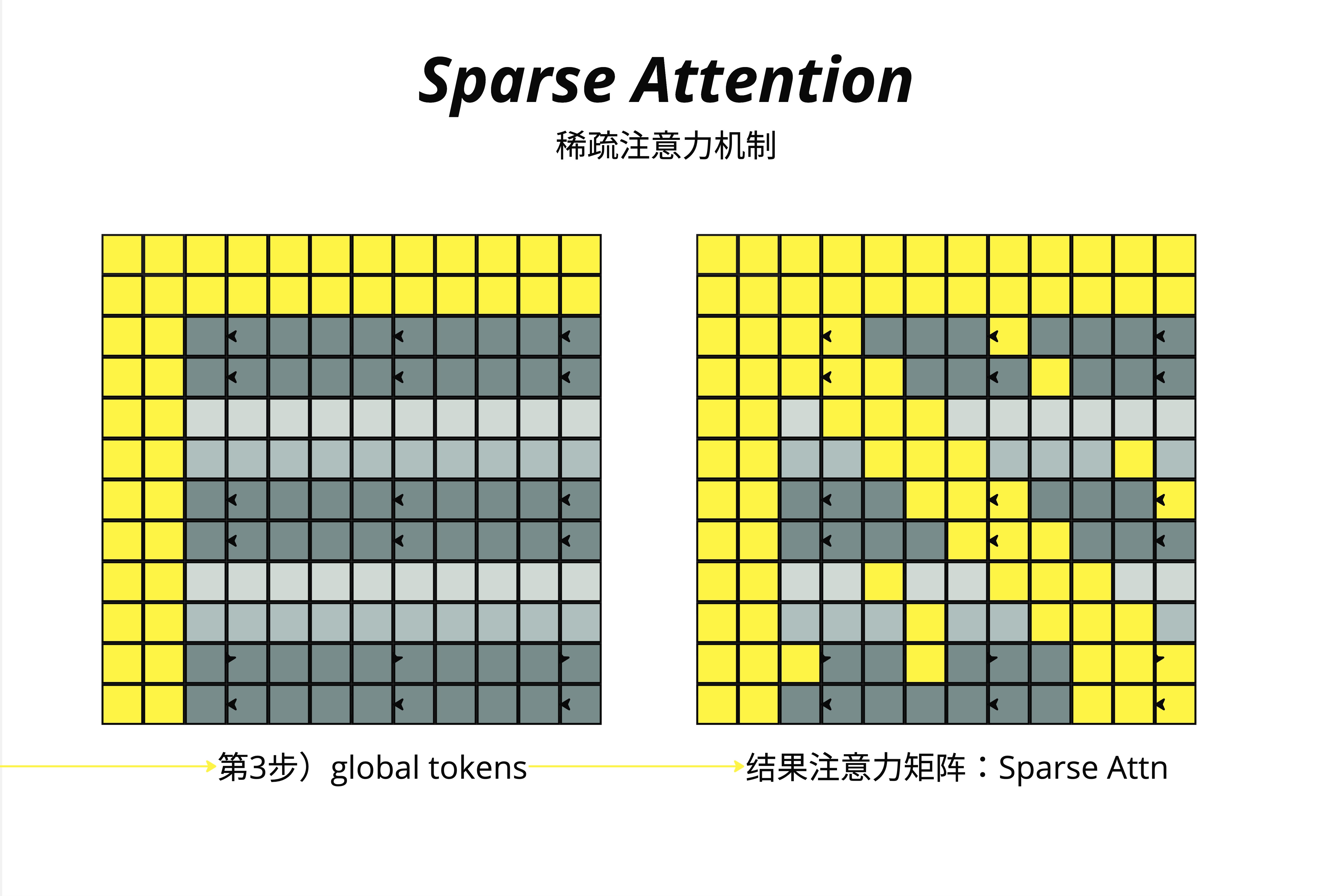
全局注意力与最终稀疏矩阵

第 3 步：Global Tokens

选择某些特殊位置作为"全局枢纽"。图中可以看到，某些行和列被完全填充为黄色——这些位置的 token 可以看到所有其他 token，同时也被所有其他 token 看到。

最终结果：Sparse Attention 矩阵

将三种模式叠加，得到最终的稀疏注意力矩阵。黄色区域是需要计算注意力的位置，灰色区域直接跳过。

24.3.2 BigBird：Random + Window + Global = 强大

BigBird（由 Google 提出）是 Sparse Attention 的经典实现，它组合了三种稀疏模式：

BigBird Attention = Random + Window + Global
BigBird 架构

从图中可以清晰看到：

  • Random（左下）：稀疏的随机连接，用图论的话说就是"随机边"
  • Window（中下）：环形的邻居连接，每个节点连接其相邻节点
  • Global（右下）：星形的全局连接，中心节点连接所有其他节点
  • BigBird（最右）：三者的组合，形成一个既有局部性又有全局性的连接图

24.3.3 复杂度分析

假设：

  • 序列长度为 n
  • 滑动窗口大小为 w
  • 全局 token 数量为 g
  • 随机连接数量为 r

则 BigBird 的复杂度为：

O(n × (w + g + r))

当 w, g, r 都是常数时，复杂度降为 O(n)，相比 Full Attention 的 O(n^2) 是质的飞跃！

24.3.4 Longformer vs BigBird

特性LongformerBigBird
滑动窗口有有
全局注意力任务相关的 token固定位置 + 随机
随机注意力无有
主要应用长文档理解通用 NLP
复杂度O(n)O(n)

Longformer 更简洁，BigBird 通过随机注意力提供了理论保证：任意两个 token 之间的最短路径是 O(1) 的。

24.4 Sliding Window Attention：局部性假设

24.4.1 为什么局部性假设成立？

语言具有强烈的局部性：

  • 语法依赖：主语和谓语通常相距不远
  • 指代消解：代词通常指代最近出现的名词
  • 语义连贯：相邻的句子通常在讨论同一个话题

这意味着，对于大多数 token，其最相关的信息就在附近。

24.4.2 Sliding Window 的工作原理

# 伪代码：Sliding Window Attention
def sliding_window_attention(Q, K, V, window_size):
    n = Q.shape[0]
    output = []

    for i in range(n):
        # 只关注窗口内的 token
        start = max(0, i - window_size // 2)
        end = min(n, i + window_size // 2 + 1)

        # 计算局部注意力
        local_K = K[start:end]
        local_V = V[start:end]

        scores = Q[i] @ local_K.T / sqrt(d_k)
        weights = softmax(scores)
        output.append(weights @ local_V)

    return stack(output)

24.4.3 层叠增加感受野

单层 Sliding Window 的感受野很有限。但如果我们堆叠多层呢？

假设窗口大小为 w=5：

  • 第 1 层后：每个 token 能"看到" 5 个 token
  • 第 2 层后：每个 token 能"看到" 9 个 token
  • 第 L 层后：每个 token 能"看到" 1 + L×(w-1) 个 token

12 层 Transformer 配合 w=512 的窗口，理论感受野可达 6000+ tokens！

24.4.4 Mistral 的 Sliding Window 实践

Mistral 7B 使用了 Sliding Window Attention，窗口大小为 4096。结合 32 层的深度，实际感受野足够处理大多数任务。

关键技巧：Rolling Buffer KV Cache

传统 KV Cache：存储所有历史 token 的 K, V
Rolling Buffer：只存储最近 window_size 个 token 的 K, V

这使得推理时的显存占用恒定，不随对话长度增长！

24.5 Linear Attention：从 O(n^2) 到 O(n)

24.5.1 标准 Attention 的数学

回顾标准 Attention 的计算：

Attention(Q, K, V) = softmax(Q @ K^T / sqrt(d_k)) @ V

计算顺序是：

  1. Q @ K^T → N x N 矩阵（这是 O(n^2) 的来源）
  2. softmax → N x N 矩阵
  3. 结果 @ V → N x d 矩阵

24.5.2 矩阵乘法的结合律

这里有一个关键观察：矩阵乘法满足结合律！

(Q @ K^T) @ V = Q @ (K^T @ V)

如果我们能先计算 K^T @ V，就能避免生成 N x N 的中间矩阵：

  • K^T @ V → d x d 矩阵
  • Q @ 结果 → N x d 矩阵

复杂度从 O(n^2 × d) 降到 O(n × d^2)！

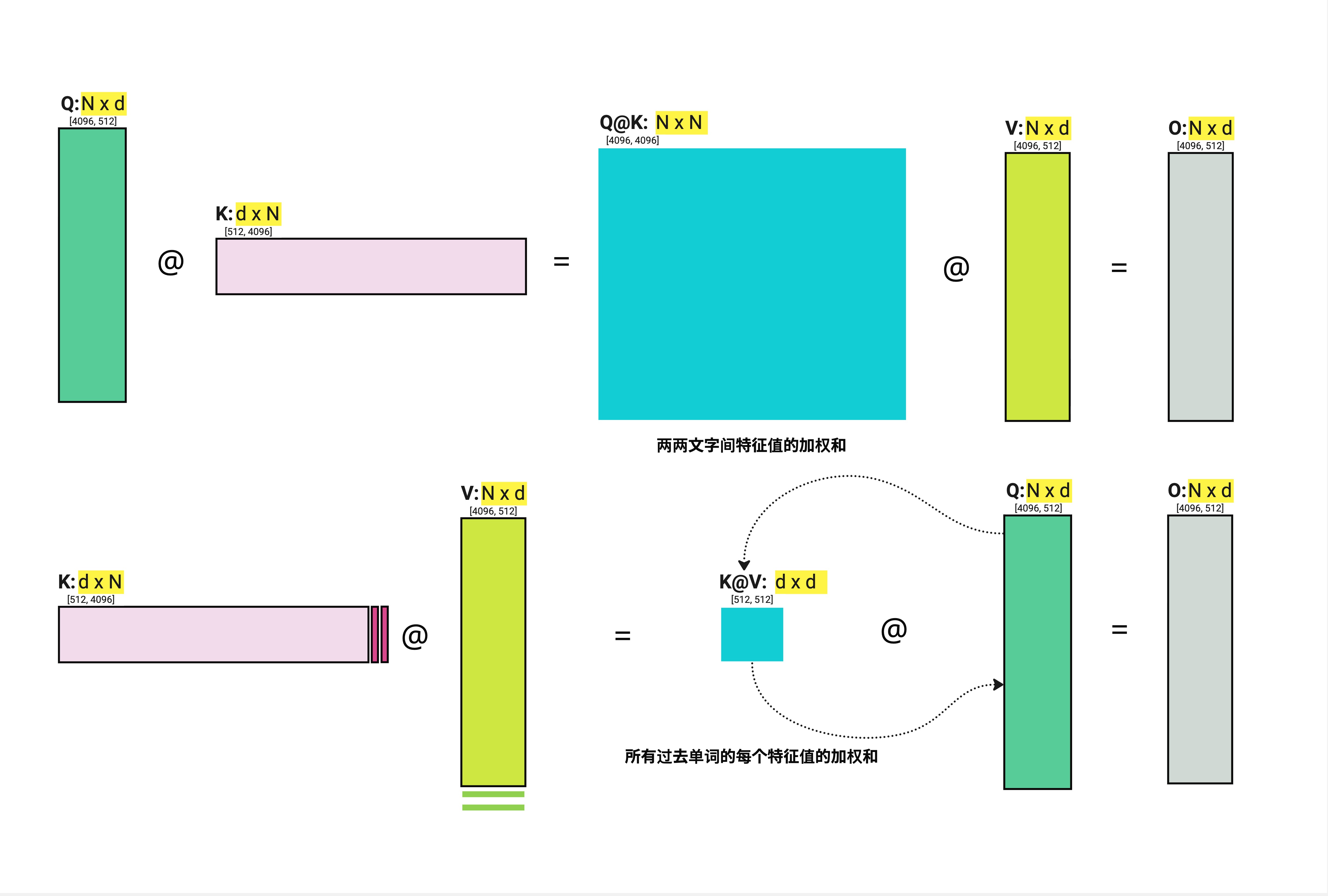
Linear Attention 原理

图中上半部分展示了标准的 Dot-Product Attention：

  • Q (N x d) @ K^T (d x N) = N x N 矩阵（青色大方块，代表"两两文字间特征值的加权和"）
  • 结果 @ V = 输出

图中下半部分展示了 Linear Attention：

  • K^T (d x N) @ V (N x d) = d x d 矩阵（青色小方块，代表"所有过去单词的每个特征值的加权和"）
  • Q @ 结果 = 输出

关键区别：中间矩阵从 N x N 变成了 d x d。当 N >> d 时，这是巨大的节省！

24.5.3 Softmax 的问题

但这里有个问题：标准 Attention 中间有个 softmax，它破坏了结合律。

softmax(Q @ K^T) @ V ≠ Q @ softmax(K^T) @ V

Linear Attention 的解决方案：用核函数（Kernel Function）替代 softmax。

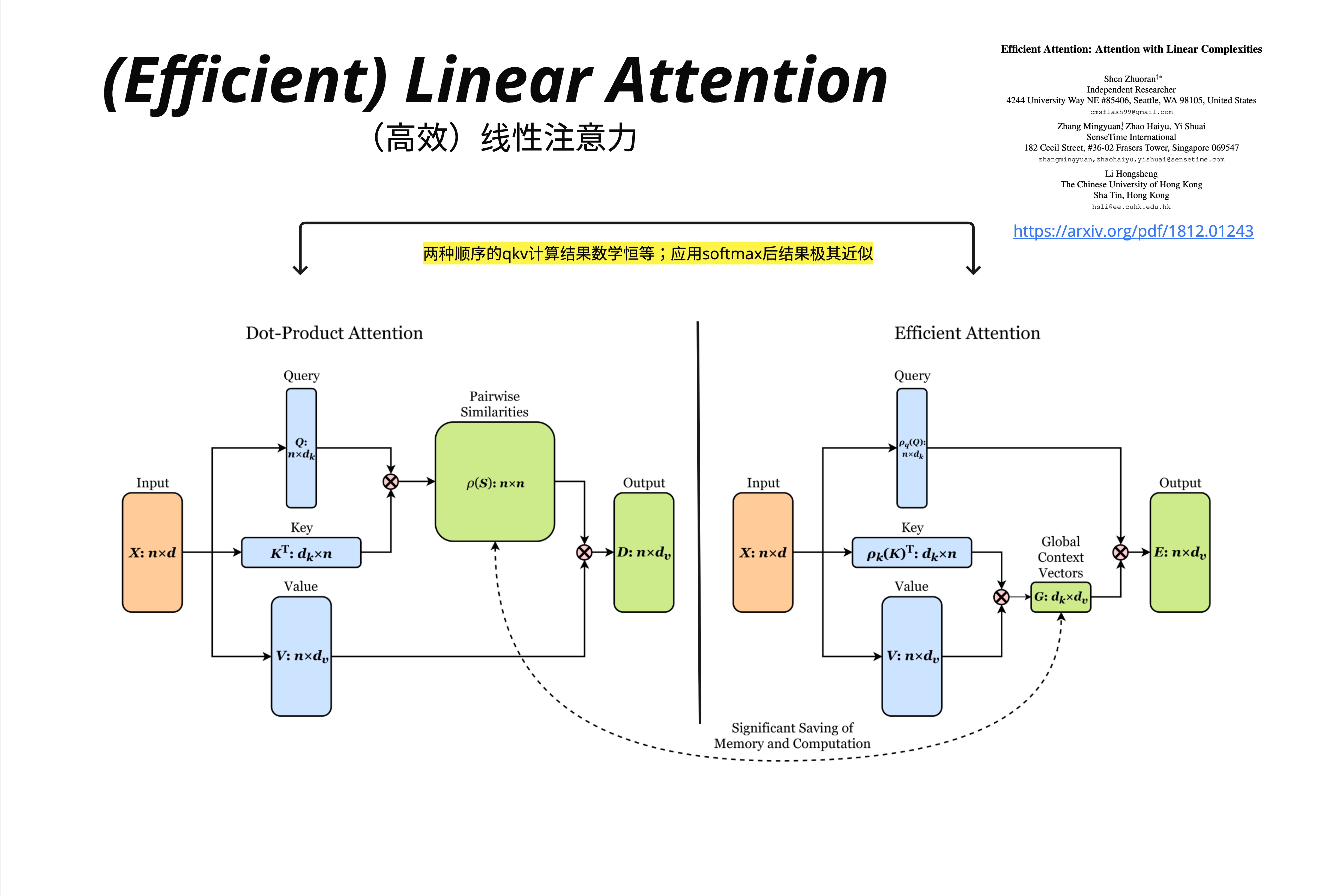
Efficient Linear Attention 论文

Efficient Attention 论文（arXiv: 1812.01243）提出：

标准 Attention: softmax(Q @ K^T) @ V
Linear Attention: φ(Q) @ φ(K)^T @ V = φ(Q) @ (φ(K)^T @ V)

其中 φ 是一个特征映射函数。论文指出："两种顺序的 QKV 计算结果数学恒等；应用 softmax 后结果极其近似"。

24.5.4 Linear Attention 的实现

# 伪代码：Linear Attention
def linear_attention(Q, K, V, feature_map):
    """
    Q, K, V: [batch, seq_len, d_model]
    feature_map: 特征映射函数，如 elu(x) + 1
    """
    # 应用特征映射
    Q_prime = feature_map(Q)  # [batch, seq_len, d_model]
    K_prime = feature_map(K)  # [batch, seq_len, d_model]

    # 先计算 K^T @ V（关键！）
    KV = einsum('bnd,bnm->bdm', K_prime, V)  # [batch, d_model, d_model]

    # 再计算 Q @ (K^T @ V)
    output = einsum('bnd,bdm->bnm', Q_prime, KV)  # [batch, seq_len, d_model]

    # 归一化
    Z = einsum('bnd,bd->bn', Q_prime, K_prime.sum(dim=1))
    output = output / Z.unsqueeze(-1)

    return output

24.5.5 Linear Attention 的局限

Linear Attention 并非完美：

  1. 表达能力下降：去掉 softmax 后，注意力分布的"尖锐度"降低
  2. 训练不稳定：某些核函数会导致数值问题
  3. 实际效果：在很多任务上不如标准 Attention

这也是为什么 Linear Attention 并未成为主流的原因。但它的思想——改变计算顺序来降低复杂度——启发了后续很多工作。

24.6 Infini Attention：无限上下文的终极方案

24.6.1 问题：KV Cache 的线性增长

即使使用了 Sliding Window，传统方法在处理超长上下文时仍有问题：

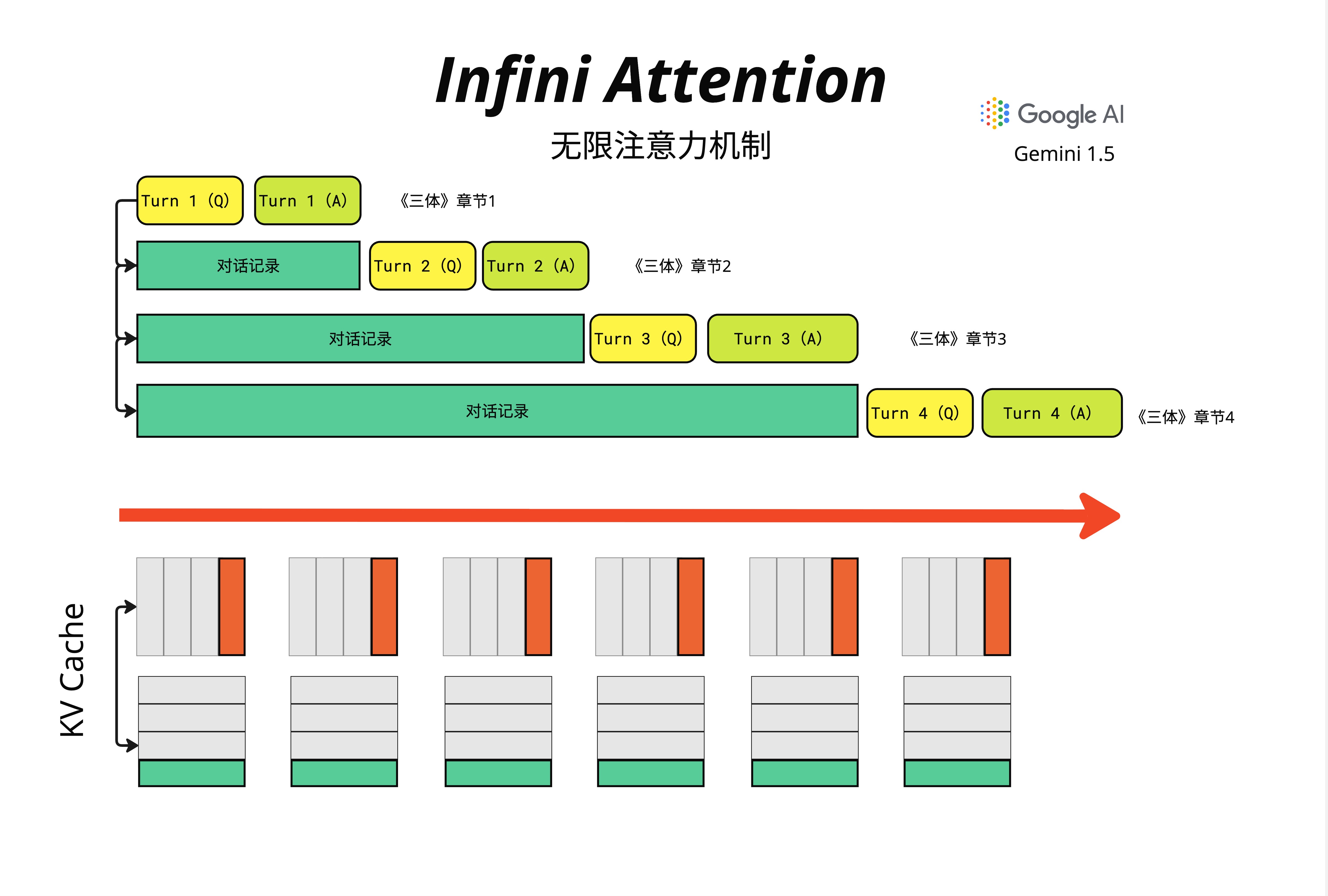
Infini Attention 对话流程

图中展示了一个阅读《三体》的场景：

  • Turn 1：读《三体》章节 1
  • Turn 2：之前的对话成为"对话记录"，继续读章节 2
  • Turn 3：对话记录更长了，继续读章节 3
  • Turn 4：对话记录越来越长...

传统的 KV Cache（图下方）会线性增长——每一轮对话都要缓存更多的 K 和 V。当对话持续很久或者需要处理整本书时，显存会爆炸。

24.6.2 Infini Attention 的核心思想

Google 在 2024 年提出的 Infini Attention 给出了一个优雅的解决方案：

用固定大小的"压缩记忆"来存储无限长的历史信息。

核心架构如下：

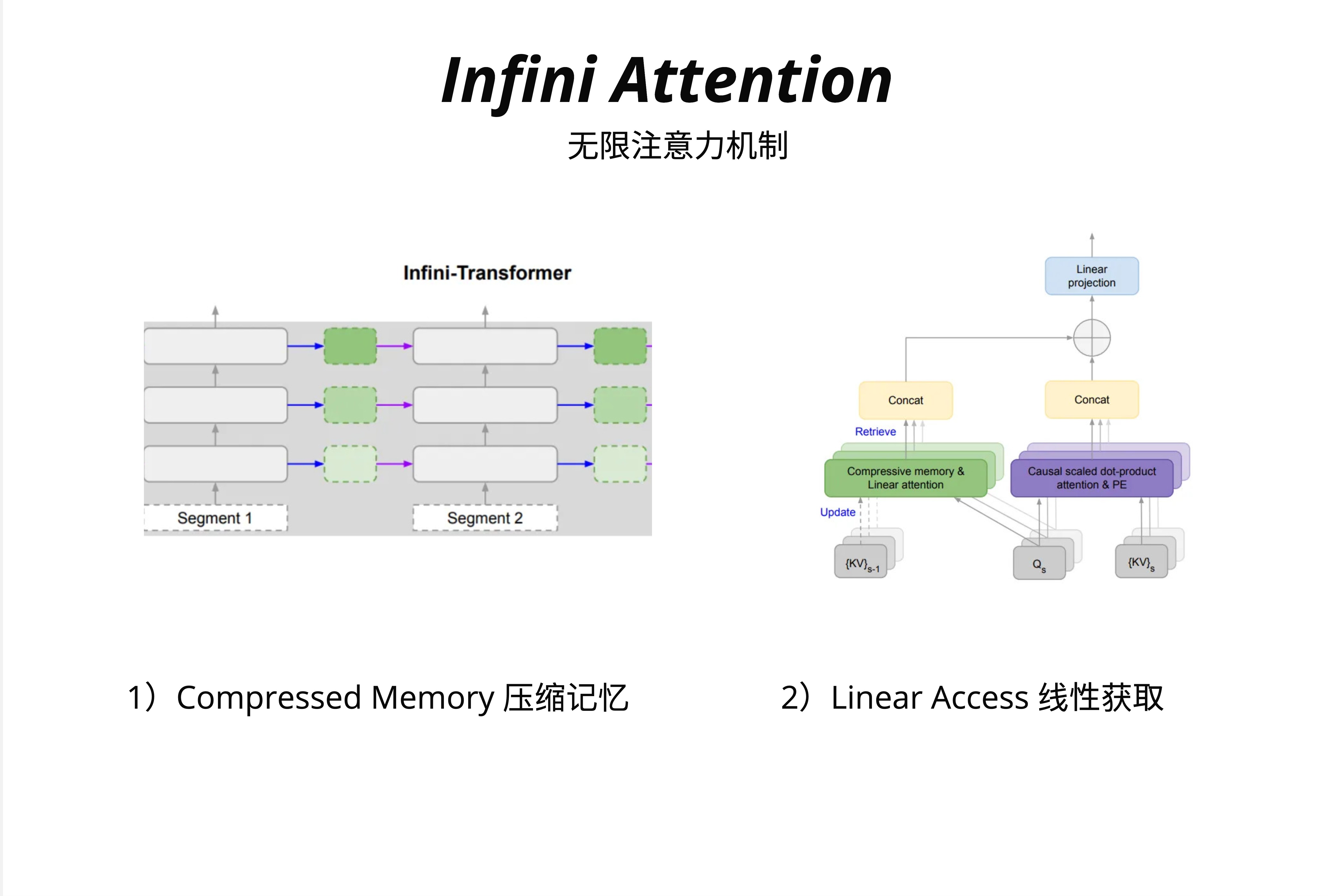
Infini-Transformer 架构

Infini-Transformer 有两个关键组件：

1. Compressed Memory（压缩记忆）

左侧展示了整体架构：输入被分成多个 Segment，每个 Segment 处理后，其信息被压缩并传递给下一个 Segment。绿色虚线框表示压缩后的记忆，它的大小是固定的，不随历史长度增长。

2. Linear Access（线性访问）

右侧展示了单个 Attention 层的内部结构：

  • 当前 Segment 的 Q、K、V 进入系统
  • 同时，前一个 Segment 的压缩记忆 {KV}_{s-1} 也参与计算
  • 通过 "Compressive memory & Linear attention" 模块，从压缩记忆中检索（Retrieve）信息
  • 通过 "Causal scaled dot-product attention" 处理当前 Segment 的局部信息
  • 两者 Concat 后，通过 Linear projection 输出
  • 同时，当前 Segment 的信息被压缩（Update）到记忆中，供下一个 Segment 使用

24.6.3 压缩记忆的数学原理

Infini Attention 使用了 Linear Attention 的思想来实现压缩记忆。

回忆 Linear Attention：

Output = Q @ (K^T @ V) / (Q @ K^T @ 1)

这里 K^T @ V 是一个 d x d 的矩阵，它压缩了所有历史 token 的信息！

Infini Attention 的关键洞察：我们可以增量更新这个压缩矩阵：

# 伪代码：Infini Attention 的记忆更新
class InfiniAttention:
    def __init__(self, d_model):
        # 压缩记忆：固定大小的 d x d 矩阵
        self.memory = zeros(d_model, d_model)
        self.normalizer = zeros(d_model)

    def forward(self, Q, K, V):
        # 1. 从压缩记忆中检索（使用 Linear Attention）
        memory_output = Q @ self.memory / (Q @ self.normalizer + eps)

        # 2. 当前 segment 的局部注意力（标准 Attention）
        local_output = standard_attention(Q, K, V)

        # 3. 融合两者
        beta = sigmoid(learned_gate)  # 可学习的门控
        output = beta * memory_output + (1 - beta) * local_output

        # 4. 更新压缩记忆（增量式）
        self.memory = self.memory + K.T @ V
        self.normalizer = self.normalizer + K.sum(dim=0)

        return output

24.6.4 为什么这能实现"无限"？

关键在于：压缩记忆的大小是固定的（d x d），与历史长度无关。

无论你处理了 1 万、10 万还是 100 万个 token，memory 矩阵的大小始终是 d_model x d_model。

这就像人类的记忆：我们不可能记住生活中的每一个细节，但我们会不断压缩和更新我们的记忆，保留最重要的信息。

24.6.5 Gemini 1.5：Infini Attention 的实战验证

Gemini 1.5 与 Infini Attention

Google 在 Gemini 发布几周后就推出了支持 1M Token 上下文的 Gemini 1.5，被认为使用了 Infini Attention 技术。

图中列出了 Infini Attention 的优势与局限性：

优势：

  • 把"过去"的信息压缩成"重点总结"来实现无限上下文窗口
  • 不需要重新训练基座模型（可以通过微调实现）

局限性：

  • 不可避免的信息丢失（压缩必然伴随信息损失）

24.6.6 Infini Attention vs 其他方法

方法复杂度显存占用信息损失实现难度
Full AttentionO(n^2)O(n^2)无简单
Sparse AttentionO(n)O(n)轻微中等
Linear AttentionO(n)O(n)中等中等
Infini AttentionO(1)*O(1)*有压缩损失复杂

*注：O(1) 是指相对于历史长度；每个 segment 内部仍有计算开销。

24.7 技术组合：实现超长上下文的完整方案

24.7.1 不是非此即彼

在实际应用中，这些技术往往是组合使用的：

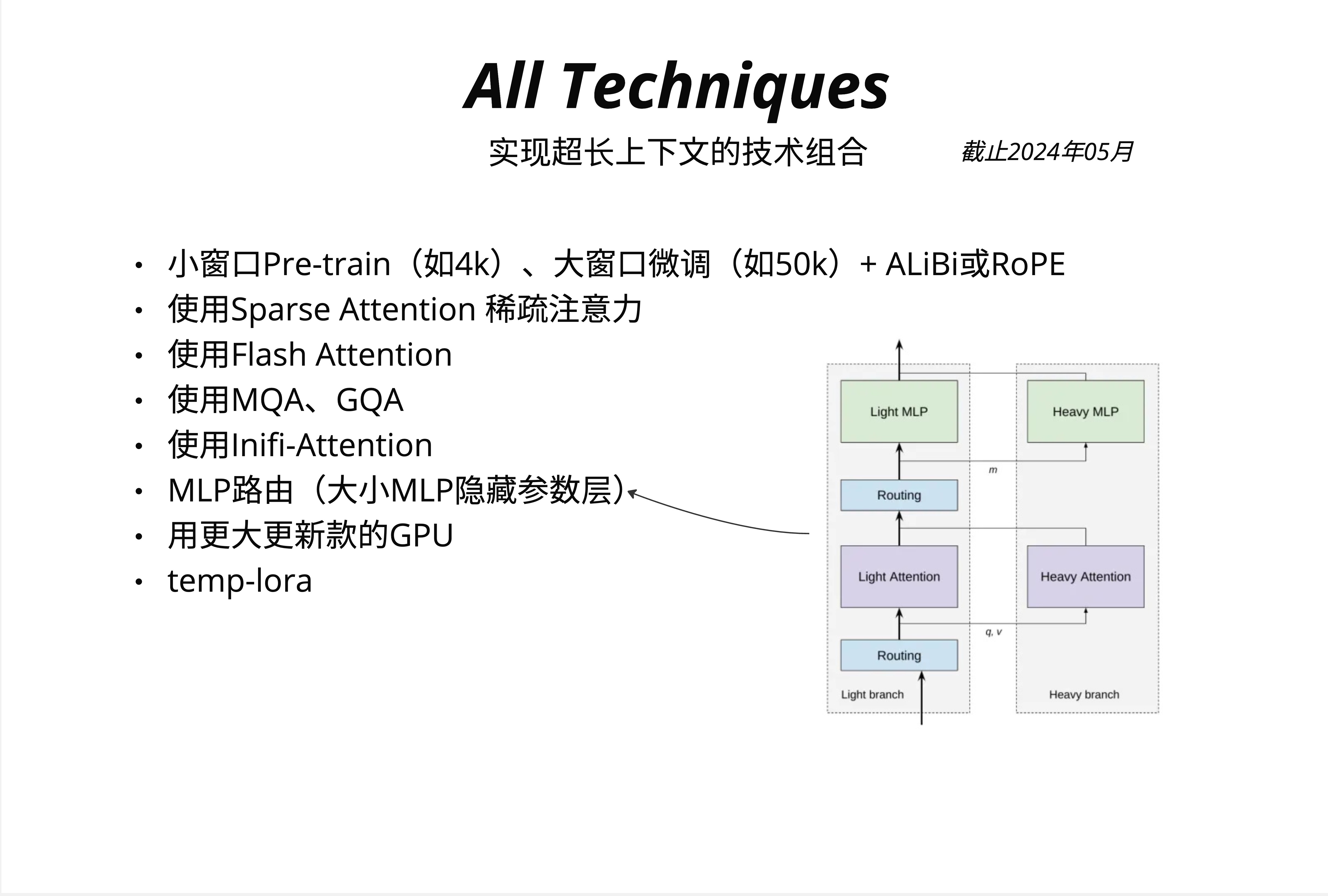
所有技术组合

截至 2024 年 5 月，实现超长上下文的主流技术组合包括：

  1. 小窗口 Pre-train + 大窗口微调 + ALiBi/RoPE

    • 预训练时使用较小窗口（如 4k）
    • 微调时扩展到更大窗口（如 50k）
    • 使用可外推的位置编码（ALiBi 或 RoPE）

  2. 使用 Sparse Attention 稀疏注意力

    • BigBird 风格的组合稀疏模式
    • 或 Longformer 风格的窗口 + 全局注意力

  3. 使用 Flash Attention

    • 不改变数学计算，但大幅降低显存占用
    • 几乎是现代 LLM 的标配

  4. 使用 MQA、GQA

    • 减少 KV Cache 的显存占用
    • 详见第 23 章

  5. 使用 Infini-Attention

    • 实现理论上无限的上下文窗口

  6. MLP 路由（大小 MLP 隐藏参数层）

    • 图中右侧展示了 Light/Heavy branch 的路由架构
    • 简单 token 走 Light Attention + Light MLP
    • 复杂 token 走 Heavy Attention + Heavy MLP

  7. 用更大更新款的 GPU

    • 最直接但最昂贵的方案

  8. temp-lora

    • 临时性的 LoRA 适配器

24.7.2 选择建议

根据你的具体需求选择合适的技术组合：

场景 1：处理长文档（10k-50k tokens）

推荐：Flash Attention + GQA + Sliding Window
原因：成熟稳定，效果好

场景 2：超长文档（50k-200k tokens）

推荐：Flash Attention + Sparse Attention + RoPE/ALiBi
原因：需要更激进的稀疏化

场景 3：极长上下文（200k+ tokens）或持续对话

推荐：Infini Attention + Flash Attention
原因：只有压缩记忆才能 handle 无限增长

24.8 手算示例：理解稀疏模式的效果

24.8.1 Full Attention 计算量

假设序列长度 N = 8，维度 d = 4。

Full Attention 需要计算：

  • Q @ K^T：(8×4) @ (4×8) → 64 个输出元素，每个需要 4 次乘法 = 256 次乘法
  • 结果 @ V：(8×8) @ (8×4) → 32 个输出元素，每个需要 8 次乘法 = 256 次乘法
  • 总计约 512 次乘法

24.8.2 Sliding Window（w=3）计算量

每个位置只看 3 个邻居：

  • 每个位置 Q @ K^T：3 个 key，每个需要 4 次乘法 = 12 次
  • 8 个位置：8 × 12 = 96 次乘法
  • V 的加权和：8 个位置 × 3 个 value × 4 维 = 96 次乘法
  • 总计约 192 次乘法

节省了 62%！（192 vs 512）

24.8.3 Linear Attention 计算量

先算 K^T @ V：4 x 8 @ 8 x 4 = 128 次乘法 再算 Q @ 结果：8 x 4 @ 4 x 4 = 128 次乘法 总计约 256 次乘法

看起来节省不多？因为 N=8 太小了。当 N=1000, d=64 时：

  • Full Attention：约 1000 x 1000 x 64 = 6400 万次乘法
  • Linear Attention：约 1000 x 64 x 64 x 2 = 800 万次乘法

节省了 87.5%！

24.9 常见误区

误区 1：Sparse Attention 会丢失重要信息

澄清：设计良好的稀疏模式（如 BigBird）通过全局 token 和随机连接，确保信息可以在整个序列中传播。实验表明，在大多数 NLP 任务上，Sparse Attention 的性能与 Full Attention 相当。

误区 2：Linear Attention 完全等价于 Standard Attention

澄清：Linear Attention 去掉了 softmax，这意味着注意力分布不再是真正的概率分布。在某些需要"尖锐"注意力的任务上，Linear Attention 表现会下降。

误区 3：Infini Attention 可以无损记住所有历史

澄清：压缩必然伴随信息损失。Infini Attention 的压缩记忆更像是"摘要"而非"完整备份"。对于需要精确回忆早期细节的任务，可能不如直接存储。

误区 4：这些技术互相排斥

澄清：这些技术是可以组合的！Flash Attention（优化实现）+ Sparse Attention（减少计算量）+ Infini Attention（处理无限历史）可以叠加使用。

24.10 本章要点回顾

  1. Full Attention 的 O(n^2) 瓶颈：序列长度增加 10 倍，计算量增加 100 倍，显存是更大的瓶颈

  2. Sparse Attention 的三种模式：

    • Random：随机连接，保证信息传播
    • Window：局部连接，捕捉局部依赖
    • Global：全局枢纽，收集分发全局信息

  3. BigBird = Random + Window + Global：组合三种模式，复杂度降为 O(n)

  4. Linear Attention 的核心技巧：改变计算顺序，先算 K^T @ V，用核函数替代 softmax

  5. Infini Attention 的创新：

    • 固定大小的压缩记忆
    • 增量更新
    • 融合局部注意力和记忆检索

  6. 实践建议：根据上下文长度需求选择合适的技术组合

24.11 延伸阅读

  1. Longformer: "Longformer: The Long-Document Transformer" (Beltagy et al., 2020)
  2. BigBird: "Big Bird: Transformers for Longer Sequences" (Zaheer et al., 2020)
  3. Linear Attention: "Efficient Attention: Attention with Linear Complexities" (Shen et al., 2018)
  4. Infini Attention: "Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention" (Google, 2024)
  5. Flash Attention: 见第 21 章
  6. Mistral Sliding Window: Mistral 7B Technical Report

24.12 下一章预告

我们已经讨论了如何处理长序列。下一章，我们将深入探讨位置编码的革新——从绝对位置编码到相对位置编码（RoPE、ALiBi），这些技术如何让模型在更长的序列上保持良好的外推能力。

引用本文 / Cite
Zhang, W. (2026). 第 24 章：Sparse 与 Infinite Attention. In Transformer 架构：从直觉到实现. https://waylandz.com/llm-transformer-book/第24章-Sparse与Infinite-Attention
@incollection{zhang2026transformer_第24章_Sparse与Infinite_Attention,
  author = {Zhang, Wayland},
  title = {第 24 章：Sparse 与 Infinite Attention},
  booktitle = {Transformer 架构：从直觉到实现},
  year = {2026},
  url = {https://waylandz.com/llm-transformer-book/第24章-Sparse与Infinite-Attention}
}