一句话总结:位置编码从"固定加法"演进到"旋转乘法"再到"注意力偏置",RoPE 用旋转矩阵让相对位置自然涌现,ALiBi 用线性惩罚让远距离 token 自动衰减,而 YaRN 则让模型突破训练时的上下文长度限制。
25.1 位置编码的演进全景
在第 5 章,我们学习了 Transformer 原始的 Sinusoidal 位置编码。那是 2017 年的方案。六年过去了,位置编码领域发生了翻天覆地的变化。

25.1.1 为什么需要更好的位置编码?
让我们先回顾一下 Sinusoidal 的局限性:
绝对位置编码的问题:
- 优势:计算速度较快
- 劣势:
- 文字间相对位置信息不明显
- 推理窗口受训练长度限制
传统相对位置编码(如 T5)的问题:
- 优势:可学习文字间相对信息
- 劣势:
- 计算量增大
- 部分实现方式与 KV Cache 不兼容
注意:RoPE 也是一种相对位置编码,但它的设计允许 KV Cache 正常工作——这正是 LLaMA 选择 RoPE 的原因之一。
这就引出了一个核心问题:我们能否设计一种位置编码,既能捕获相对位置信息,又能高效推理?
25.1.2 五种主流方案
目前主流的位置编码方案有五种:
| 方案 | 英文全称 | 中文名 | 代表模型 |
|---|---|---|---|
| T5 Relative | Relative Positional Embeddings | 相对位置编码 | T5 |
| Sinusoidal | Sine & Cosine Embedding Positions | 正余弦位置编码 | 原始 Transformer |
| RoPE | Rotary Position Embedding | 旋转位置编码 | LLaMA, GPT-NeoX |
| YaRN | Yet another RoPE extensioN | RoPE 扩展 | Code Llama, Qwen |
| ALiBi | Attention with Linear Bias | 线性偏置项位置编码 | BLOOM, MPT |
本章我们将深入讲解 RoPE、ALiBi 和 YaRN 这三种现代方案。
25.2 Sinusoidal 回顾:加法的局限
在深入新方案之前,让我们快速回顾 Sinusoidal 的工作方式。
25.2.1 Sinusoidal 的核心思想
Sinusoidal 位置编码的公式:
PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
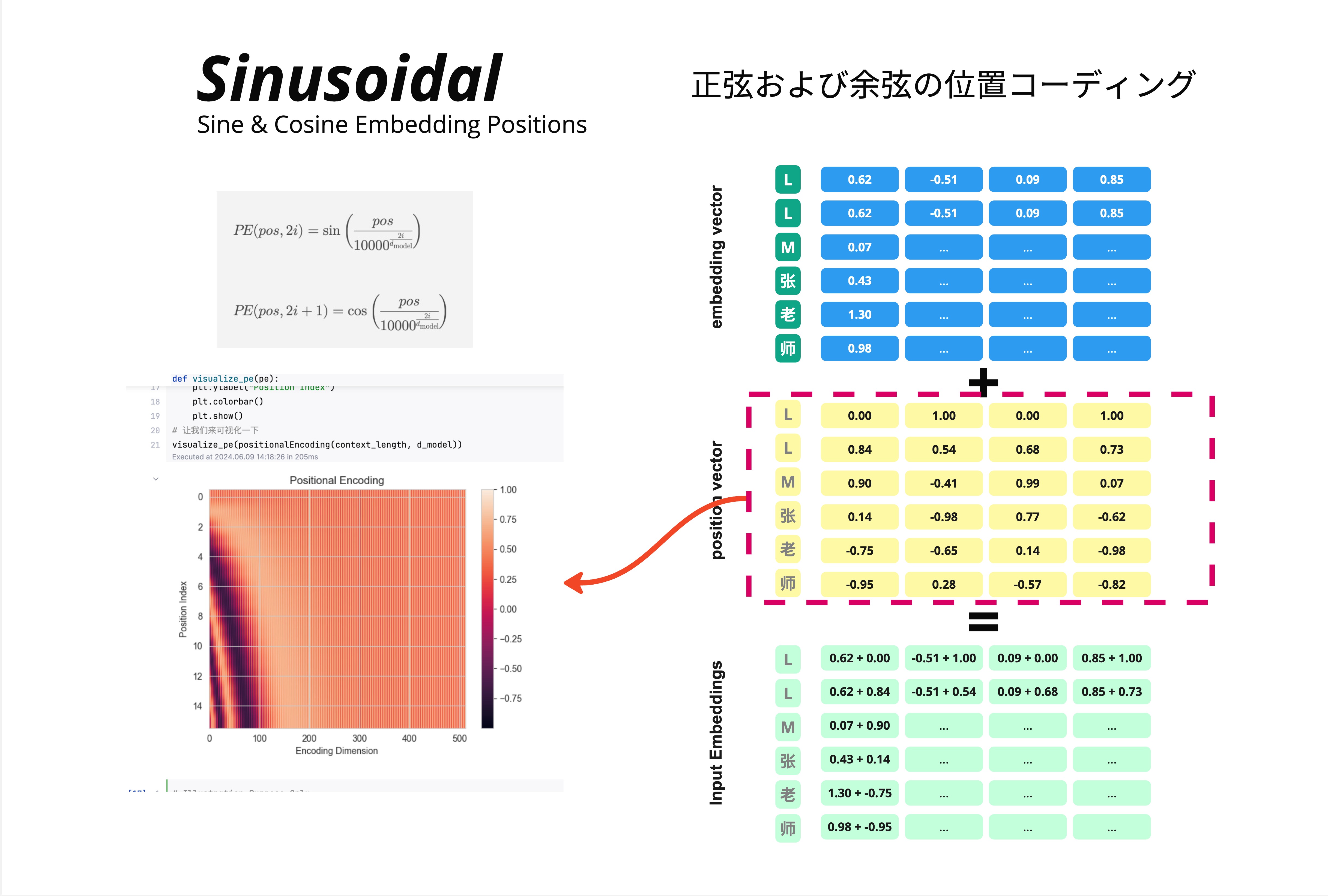
PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))工作方式很简单:把位置向量加到词向量上。
以"LLM张老师"为例:
Embedding 向量(语义信息):
| 字 | 维度1 | 维度2 | 维度3 | 维度4 |
|---|---|---|---|---|
| L | 0.62 | -0.51 | 0.09 | 0.85 |
| L | 0.62 | -0.51 | 0.09 | 0.85 |
| M | 0.07 | ... | ... | ... |
Position 向量(位置信息):
| 位置 | 维度1 | 维度2 | 维度3 | 维度4 |
|---|---|---|---|---|
| 1 | 0.00 | 1.00 | 0.00 | 1.00 |
| 2 | 0.84 | 0.54 | 0.68 | 0.73 |
| 3 | 0.90 | -0.41 | 0.99 | 0.07 |
Input Embeddings = Embedding + Position
25.2.2 为什么"加法"有局限?
关键问题在于:加法操作发生在进入 Attention 之前。
当我们计算 Q 和 K 的点积时:
Q = (x + PE_m) * W_Q
K = (x + PE_n) * W_K
Q · K = ?展开后会得到四项交叉项,位置信息和语义信息混在一起,很难解耦。
更严重的问题是:Sinusoidal 编码的是绝对位置。模型学到的是"位置 5"的模式,而不是"相距 3 个位置"的模式。当推理长度超过训练长度时,模型会遇到从未见过的绝对位置,性能急剧下降。
这就是为什么早期的 GPT 模型有严格的上下文长度限制:训练多长,就只能用多长。
25.3 RoPE:旋转位置编码
2021 年,苏剑林提出了 RoPE(Rotary Position Embedding),彻底改变了位置编码的范式。
25.3.1 核心直觉:从加法到乘法
RoPE 的革命性想法:不再把位置信息加到词向量上,而是用旋转矩阵对 Q、K 向量进行旋转。
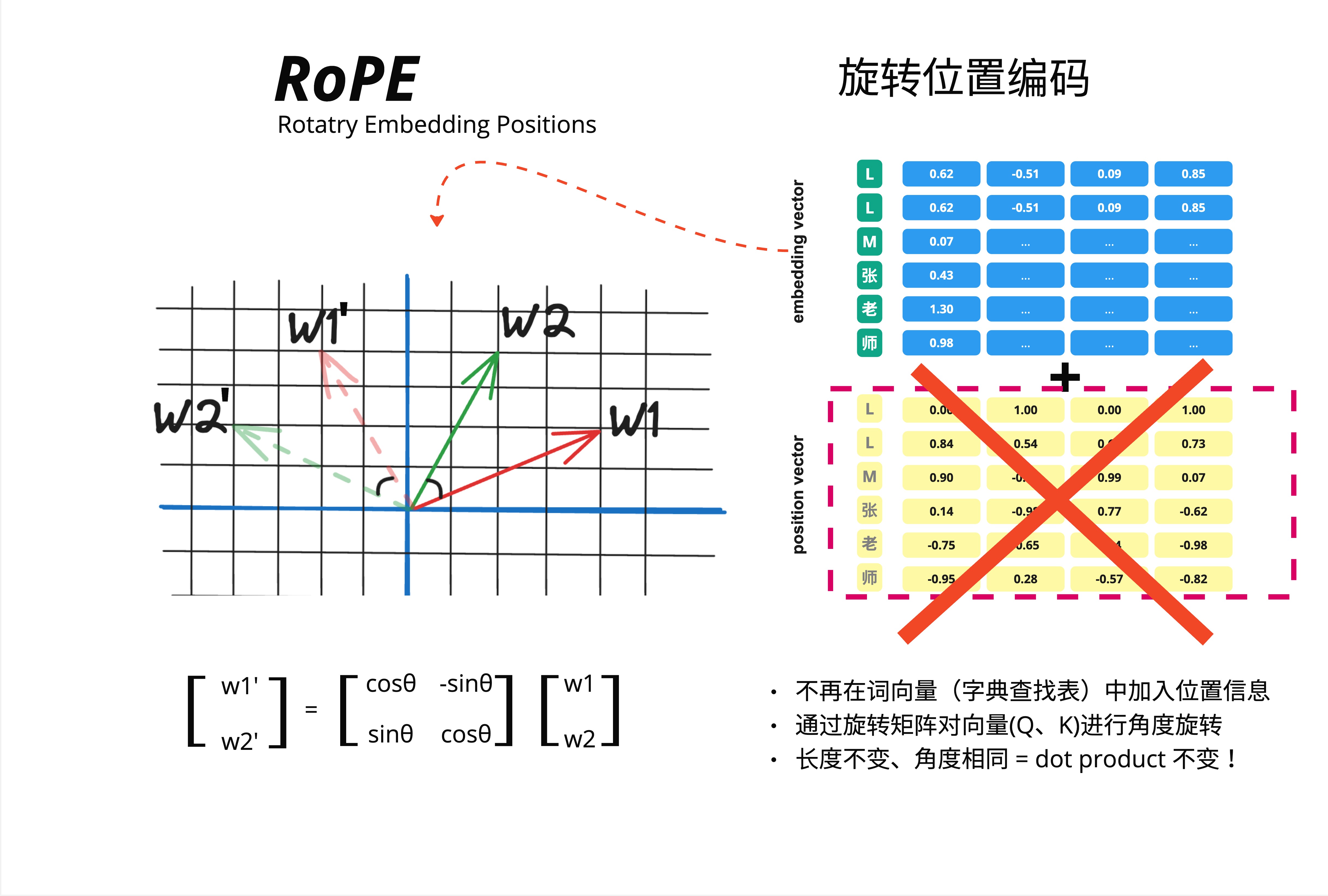
看图中的对比:
Sinusoidal(加法):
- embedding vector + position vector = input embeddings
RoPE(旋转):
- 不再在词向量(字典查找表)中加入位置信息
- 通过旋转矩阵对向量(Q、K)进行角度旋转
- 长度不变、角度相同 = dot product 不变!
这个"长度不变、角度相同"是什么意思?让我们用 2D 来理解。
25.3.2 2D 旋转的几何直觉
想象在二维平面上有两个向量 w1 和 w2:
w1' w2
\ /
\ /
w2' \/ w1
\ /
\ /如果我们把 w1 和 w2 都旋转相同的角度 theta:
- w1 变成 w1'
- w2 变成 w2'
关键观察:w1 和 w2 之间的夹角没有变!
既然夹角没变,那么它们的点积(dot product)也没变:
w1 · w2 = |w1| |w2| cos(angle)
w1' · w2' = |w1'| |w2'| cos(angle) # 相同!这就是 RoPE 的核心洞察:如果我们把位置信息编码成旋转角度,那么相对位置自然就体现在两个向量的相对旋转角度中。
25.3.3 旋转矩阵
2D 旋转矩阵的形式是:
[w1'] [cos(theta) -sin(theta)] [w1]
[w2'] = [sin(theta) cos(theta)] [w2]对于位置 m 的 token,旋转角度是 m * theta。
25.3.4 高维度的处理
真实的词向量不是 2D 的,而是 768D 或 4096D。RoPE 的处理方式是:把高维向量拆成多个 2D 子空间,每个子空间独立旋转。
假设 d=6(6 维向量),会被拆成 d/2=3 对:
- 第 1-2 维:用角度 theta_1 旋转
- 第 3-4 维:用角度 theta_2 旋转
- 第 5-6 维:用角度 theta_d/2 旋转
每对维度使用不同的基础频率,类似于 Sinusoidal 中不同维度有不同频率的思想。
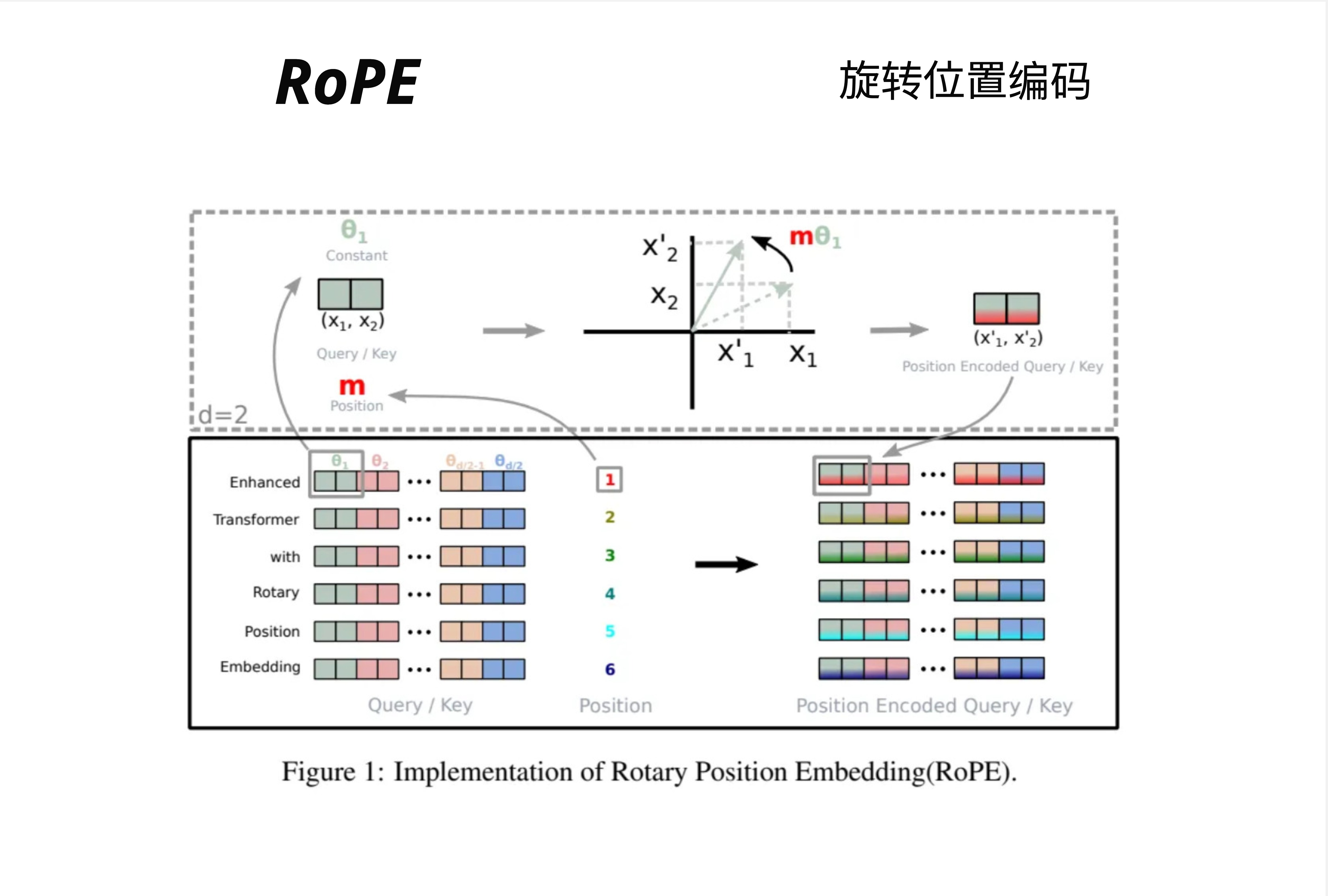
图中展示了完整的流程:
- Query/Key 向量(左侧彩色方块)
- 结合位置 m(1, 2, 3, 4, 5, 6...)
- 在 2D 平面上旋转 m * theta
- 得到 Position Encoded Query/Key(右侧彩色方块)
25.3.5 完整的旋转矩阵
对于 d 维向量,完整的旋转矩阵是一个分块对角矩阵:
[cos(m*theta_1) -sin(m*theta_1) 0 0 ... 0 0 ]
[sin(m*theta_1) cos(m*theta_1) 0 0 ... 0 0 ]
R_m = [ 0 0 cos(m*theta_2) -sin(m*theta_2) ... 0 0 ]
[ 0 0 sin(m*theta_2) cos(m*theta_2) ... 0 0 ]
[ ... ... ... ... ... ... ... ]
[ 0 0 0 0 ... cos(m*theta_d/2) -sin(m*theta_d/2)]
[ 0 0 0 0 ... sin(m*theta_d/2) cos(m*theta_d/2)]每个 2x2 块是一个独立的旋转矩阵。
25.3.6 频率的选择
论文建议使用:
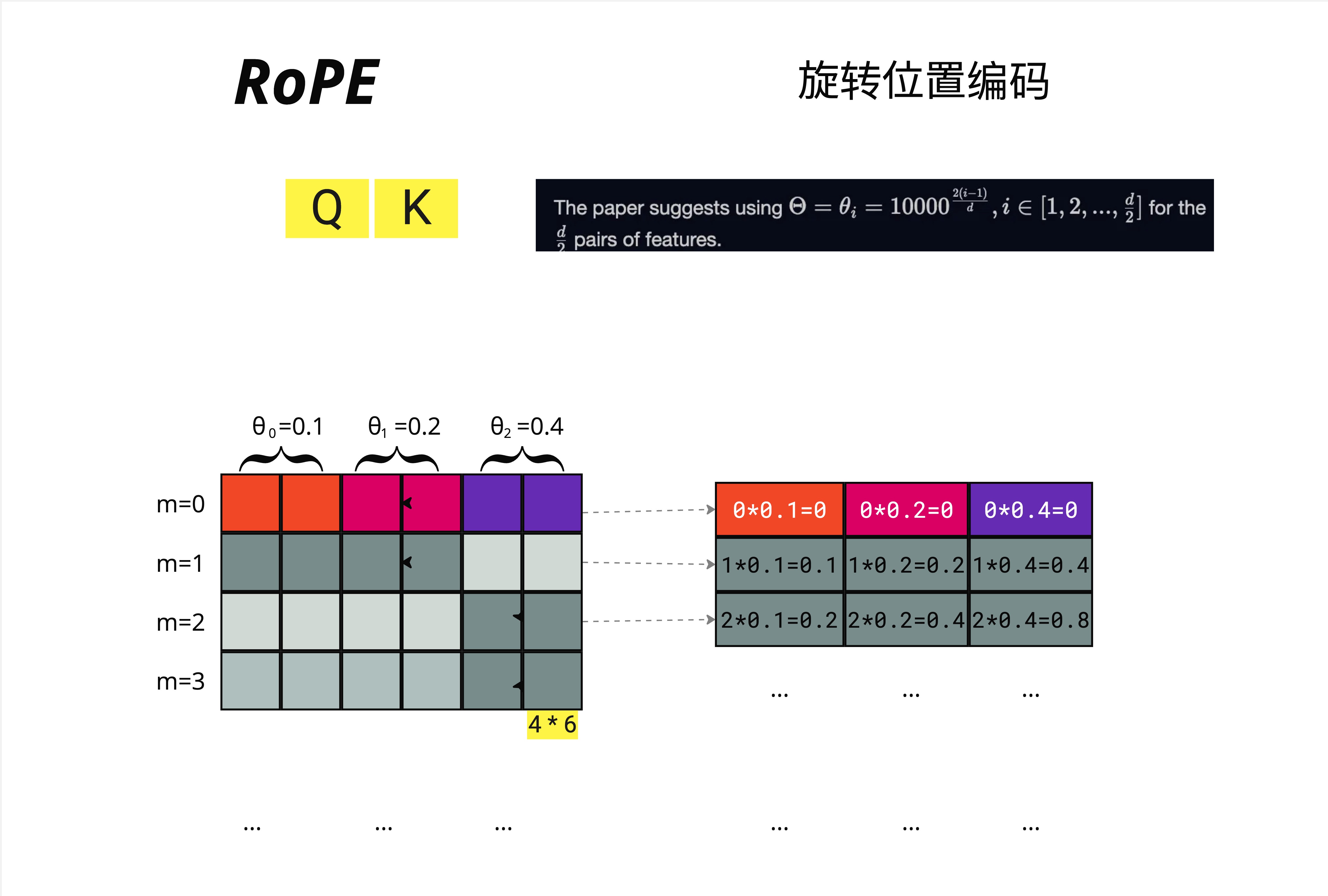
theta_i = 10000^(-2(i-1)/d), i = 1, 2, ..., d/2例如,对于 d=6 的向量:
- theta_0 = 0.1
- theta_1 = 0.2
- theta_2 = 0.4
位置 m 对应的旋转角度:
| 位置 m | 第 1 对 | 第 2 对 | 第 3 对 |
|---|---|---|---|
| m=0 | 0*0.1=0 | 0*0.2=0 | 0*0.4=0 |
| m=1 | 1*0.1=0.1 | 1*0.2=0.2 | 1*0.4=0.4 |
| m=2 | 2*0.1=0.2 | 2*0.2=0.4 | 2*0.4=0.8 |
| m=3 | ... | ... | ... |
25.3.7 为什么 RoPE 能编码相对位置?
这是 RoPE 最精妙的地方。
假设位置 m 的 Query 是 q_m,位置 n 的 Key 是 k_n。
应用 RoPE 后:
- q_m' = R_m * q_m(旋转 m * theta)
- k_n' = R_n * k_n(旋转 n * theta)
计算注意力分数时:
q_m' · k_n' = (R_m * q_m)^T * (R_n * k_n)
= q_m^T * R_m^T * R_n * k_n
= q_m^T * R_(n-m) * k_n关键来了:R_m^T * R_n = R_(n-m),这是旋转矩阵的性质!
所以最终的注意力分数只依赖于相对位置 (n-m),而不是绝对位置 m 和 n!
这就是 RoPE 的魔法:通过旋转操作,相对位置信息自然涌现,无需显式计算。
25.3.8 RoPE 的长期衰减特性
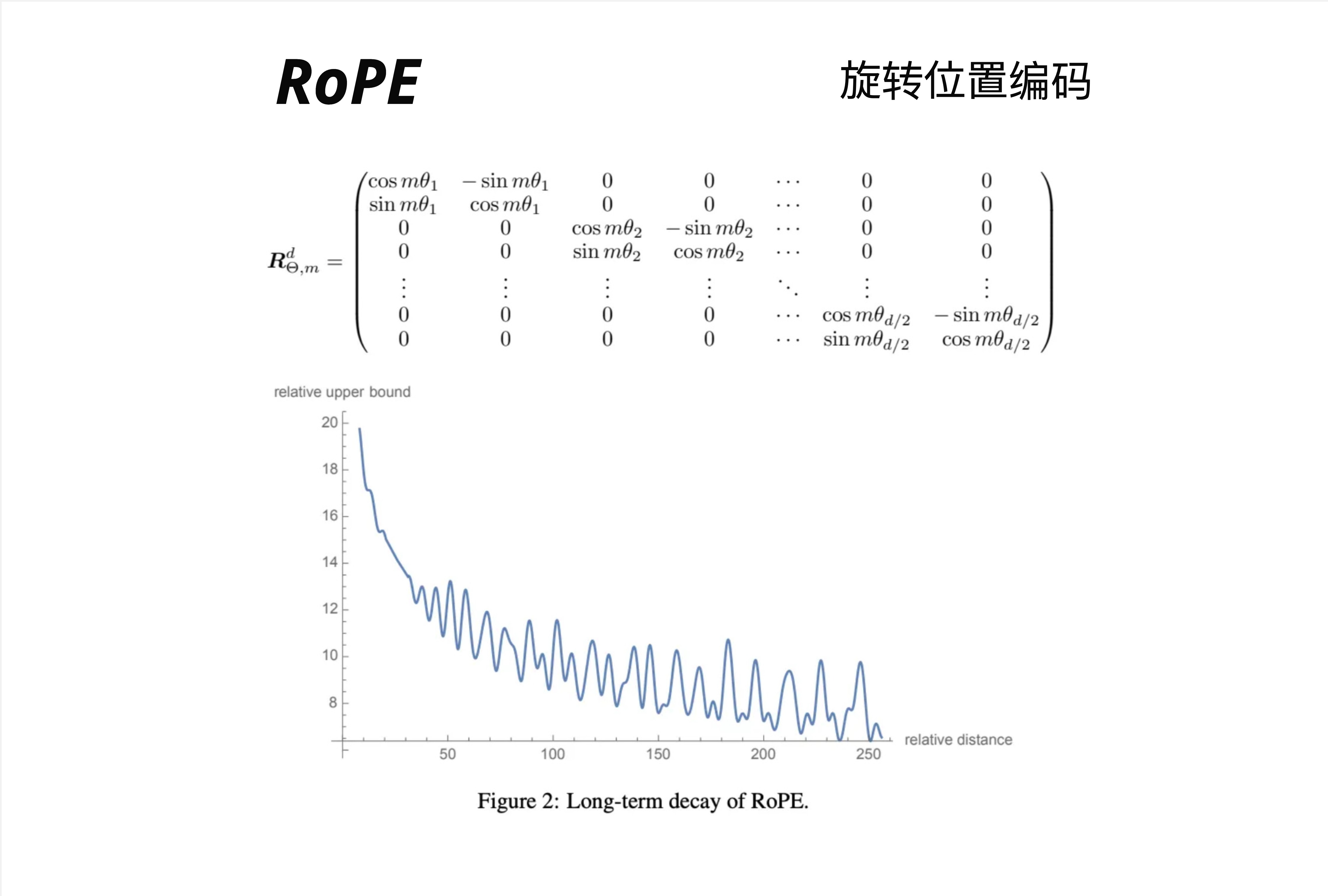
图中展示了 RoPE 的一个重要特性:随着相对距离增加,注意力分数的上界会衰减。
这意味着:
- 相邻的 token 可以获得更高的注意力
- 距离很远的 token 注意力会自然减弱
这符合语言的局部性原理:相邻的词通常关系更密切。
25.3.9 RoPE 可视化:热力图
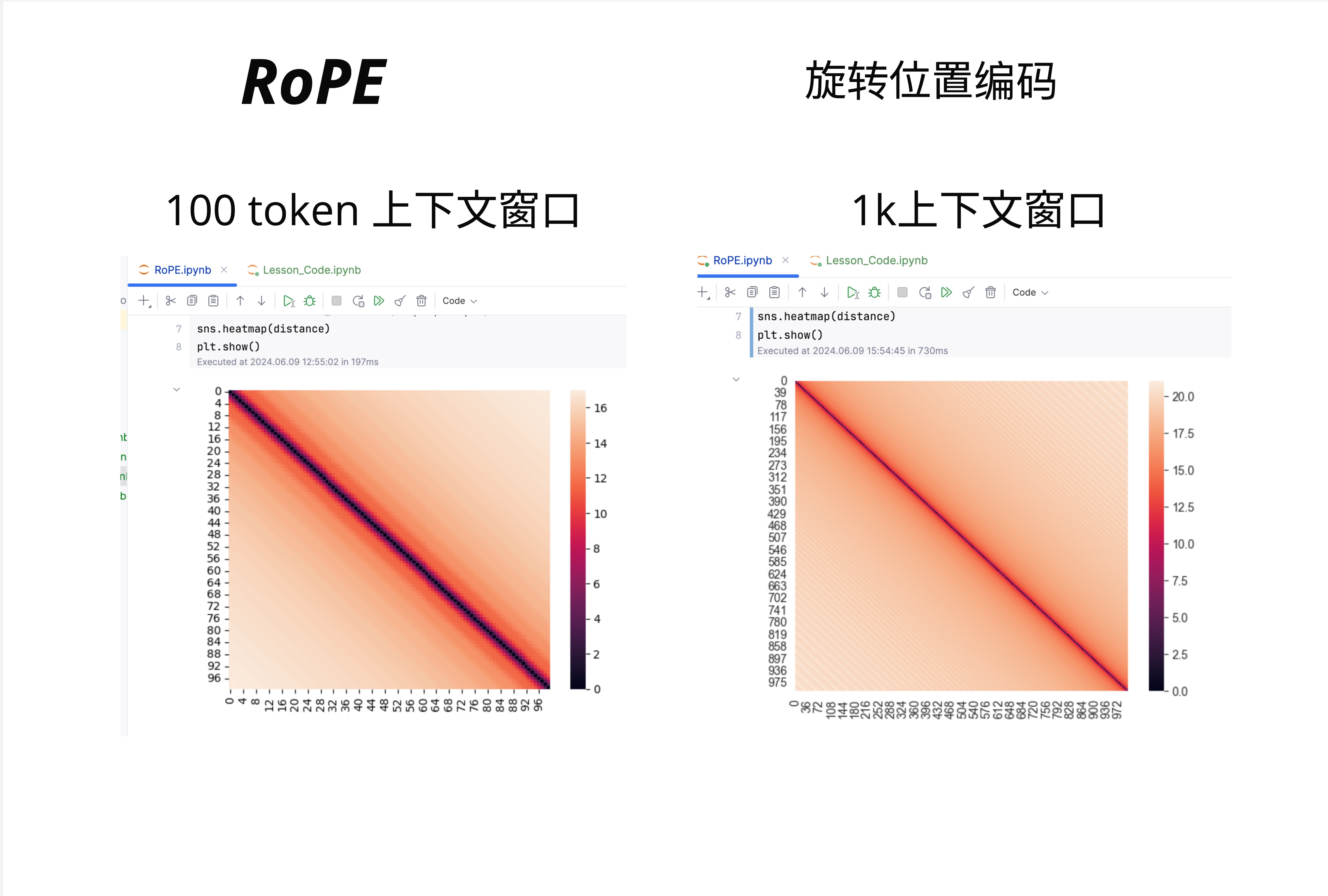
图中展示了不同上下文长度下的 RoPE 距离热力图:
- 100 token 上下文窗口
- 1k 上下文窗口
- 10k 上下文窗口
可以看到:
- 对角线附近颜色深(相对距离小,注意力高)
- 远离对角线颜色浅(相对距离大,注意力低)
- 随着上下文变长,整体模式保持一致
25.3.10 RoPE 的直观类比
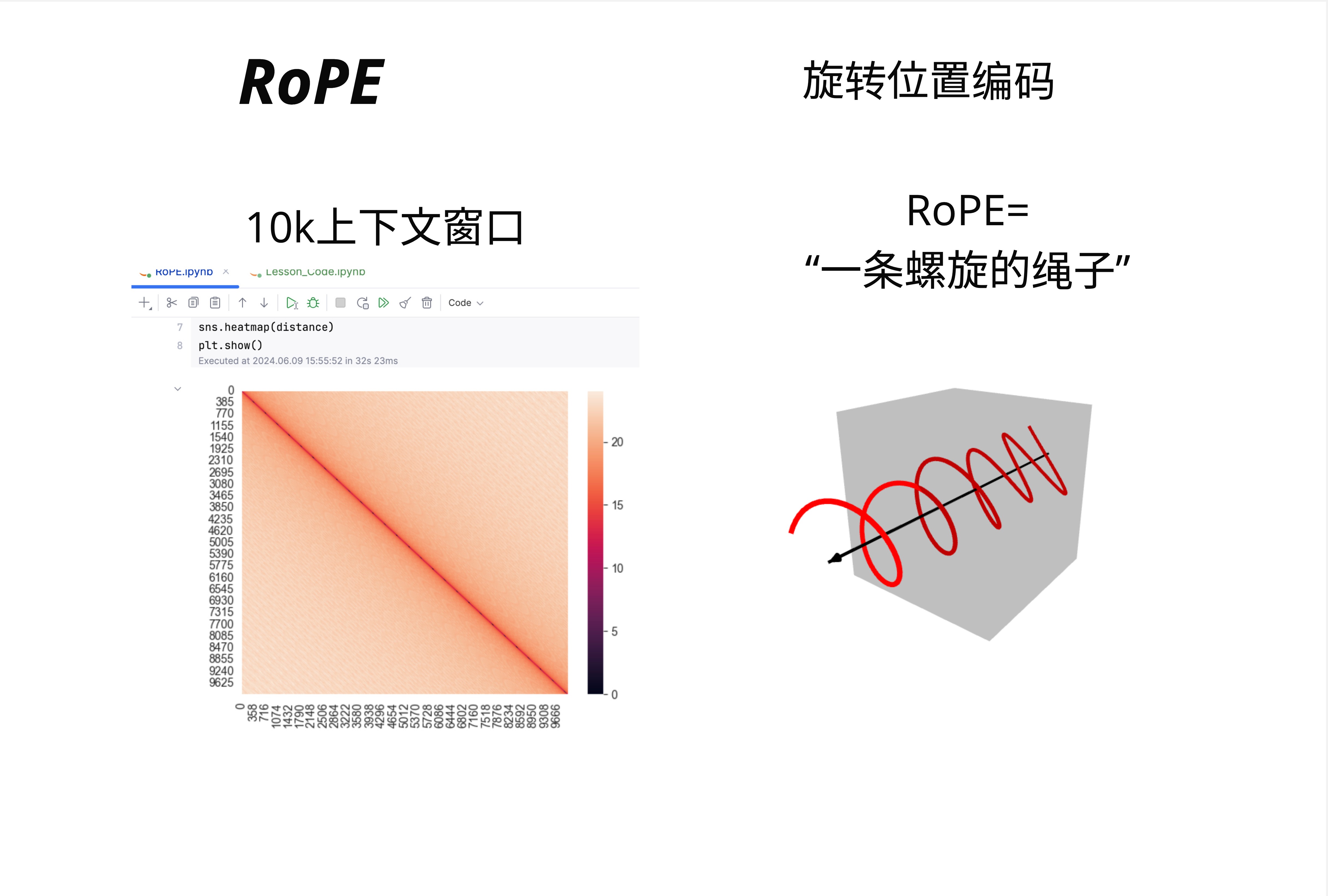
一个形象的类比:RoPE 就像一条螺旋的绳子。
- 每个位置对应绳子上的一个点
- 位置越远,旋转的角度越大
- 相邻的点之间角度差是固定的
这就是为什么 RoPE 能编码相对位置:你只需要知道两个点之间转了多少圈,就知道它们相距多远。
25.4 ALiBi:线性偏置的简洁之美
2021 年,Press 等人提出了另一种完全不同的方案:ALiBi(Attention with Linear Biases)。
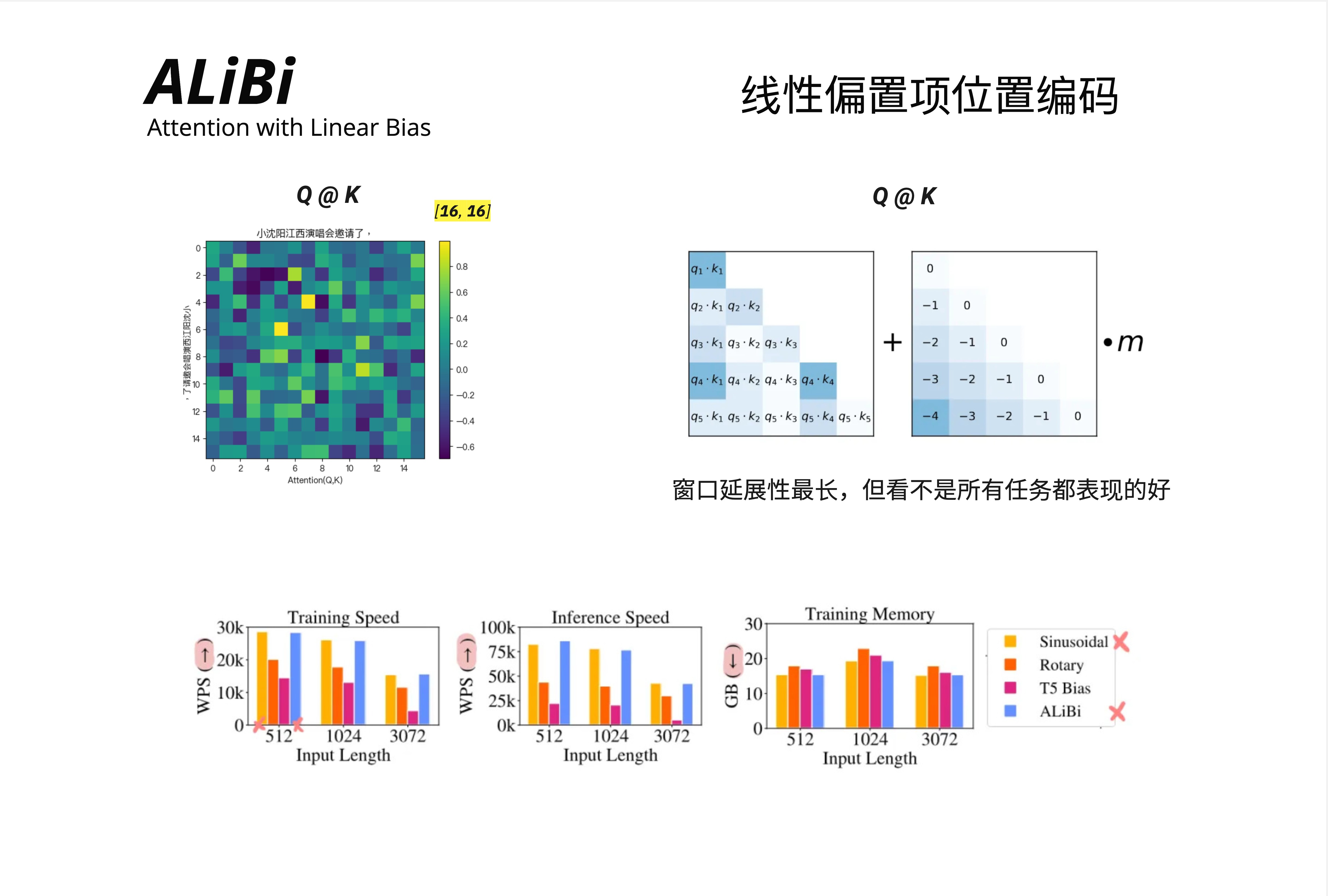
25.4.1 核心思想:惩罚远距离
ALiBi 的想法非常简洁:不修改 embedding,而是在注意力分数上加一个线性惩罚。
距离越远,惩罚越大。就这么简单。
25.4.2 数学形式
标准的注意力计算是:
Attention(Q, K, V) = softmax(Q * K^T / sqrt(d)) * VALiBi 修改为:
Attention(Q, K, V) = softmax(Q * K^T / sqrt(d) + m * bias) * V其中 bias 是一个距离矩阵:
bias = [ 0 ] (position 1)
[-1 0 ] (position 2)
[-2 -1 0] (position 3)
[-3 -2 -1 0] (position 4)
[-4 -3 -2 -1 0] (position 5)m 是一个超参数(每个注意力头不同)。
25.4.3 直觉理解
假设当前 token 在位置 5,它要计算与位置 1-5 的注意力:
| 目标位置 | 相对距离 | 偏置(m=1) | 效果 |
|---|---|---|---|
| 位置 1 | 4 | -4 | 大幅降低注意力 |
| 位置 2 | 3 | -3 | 显著降低注意力 |
| 位置 3 | 2 | -2 | 中等降低注意力 |
| 位置 4 | 1 | -1 | 轻微降低注意力 |
| 位置 5 | 0 | 0 | 不变 |
经过 softmax 后,近处的 token 自然获得更高的注意力权重。
25.4.4 为什么 ALiBi 能外推?
ALiBi 最大的优势是零样本外推能力。
原因很简单:bias 矩阵是确定性的,不需要学习。无论上下文多长,计算方式都一样。
实验表明,用 1024 长度训练的 ALiBi 模型,可以直接外推到 2048 甚至更长,几乎没有性能损失。
25.4.5 ALiBi 的优缺点
优点:
- 实现极简(几行代码)
- 训练高效(不引入额外参数)
- 外推能力强
缺点:
- 不是所有任务都表现好
- 简单的线性惩罚可能过于粗暴
- 在某些需要精确位置信息的任务上表现较差
图中的性能对比显示:
- Training Speed:ALiBi(蓝色)与其他方案相当
- Inference Speed:ALiBi 稍有优势
- Training Memory:ALiBi 内存占用较低
25.5 YaRN:扩展 RoPE 的上下文长度
RoPE 虽然优秀,但有一个问题:当推理长度超过训练长度时,性能会下降。
YaRN(Yet another RoPE extensioN)就是为了解决这个问题而生。

25.5.1 问题:外推的困境
假设模型用 4k 上下文训练,推理时遇到 8k 的输入:
- 位置 1-4000:见过,没问题
- 位置 4001-8000:从未见过的旋转角度,模型困惑
直接外推会导致注意力模式崩溃。
25.5.2 Position Interpolation(PI)
最简单的解决方案是位置插值:把 8k 的位置压缩到 4k 的范围内。
f'_W(x_m, m, theta_d) = f_W(x_m, m*L/L', theta_d)其中:
- L 是原始训练长度(4k)
- L' 是目标长度(8k)
- s = L'/L = 2(缩放因子)
位置 8000 被映射到位置 4000,模型就能理解了。
问题:高频信息丢失。相邻 token 的位置差异被压缩,精度下降。
25.5.3 NTK-Aware Interpolation
NTK-Aware 是一种更聪明的插值方式,被 Code Llama、Qwen 7B 等模型使用。
核心思想:对不同频率的维度使用不同的缩放因子。
- 低频维度:大幅缩放(它们编码长程位置信息)
- 高频维度:少量缩放(它们编码局部位置信息,需要保持精度)
25.5.4 YaRN 的完整方案
YaRN 在 PI 和 NTK 的基础上更进一步:
f'_W(x_m, m, theta_d) = f_W(x_m, g(m), h(theta_d))
关键改进:
- 位置变换函数 g(m)
- 频率变换函数 h(theta_d)
- 注意力温度调整
YaRN 的一大优势:只需要不到 0.1% 的预训练 token 数进行微调,就能扩展上下文长度。
例如:
- 原始模型:4k 上下文,用 1T token 训练
- YaRN 微调:32k 上下文,只需 ~1B token 微调
25.5.5 温度调整
YaRN 还引入了注意力温度调整:
softmax(Q_m^T * K_n / (t * sqrt(d)))其中:
sqrt(1/t) = 0.1 * ln(s) + 1s 是缩放因子。这个调整让长序列的注意力分布更加平滑。
25.6 各方案对比
25.6.1 技术对比
| 特性 | Sinusoidal | RoPE | ALiBi | YaRN |
|---|---|---|---|---|
| 位置信息注入 | 加到 embedding | 旋转 Q/K | 偏置注意力 | 旋转 Q/K |
| 编码类型 | 绝对位置 | 相对位置 | 相对位置 | 相对位置 |
| 外推能力 | 差 | 中等 | 强 | 强 |
| KV Cache 兼容 | 是 | 是 | 是 | 是 |
| 额外参数 | 无 | 无 | 无 | 无 |
| 计算开销 | 低 | 中 | 低 | 中 |
25.6.2 主流模型的选择
| 模型 | 位置编码 | 上下文长度 |
|---|---|---|
| GPT-3 | 学习式位置编码 | 2048 |
| LLaMA 1 | RoPE | 2048 |
| LLaMA 2 | RoPE | 4096 |
| Code Llama | RoPE + YaRN | 16384 |
| Mistral | RoPE | 8192 |
| BLOOM | ALiBi | 2048 |
| MPT | ALiBi | 65536 |
| Qwen | RoPE + Dynamic NTK | 8192-32768 |
| Claude | 未公开 | 100k+ |
| GPT-4 | 未公开 | 128k |
25.6.3 如何选择?
选择 RoPE 如果:
- 需要精确的位置信息
- 上下文长度适中(4k-8k)
- 想用 LLaMA 生态
选择 ALiBi 如果:
- 需要强外推能力
- 实现要简单
- 内存/计算资源有限
选择 YaRN 如果:
- 需要超长上下文(16k+)
- 已有 RoPE 模型,想扩展
- 有少量微调预算
25.7 实现细节
25.7.1 RoPE 的高效实现
直接用旋转矩阵乘法效率不高。实际实现使用复数形式:
def apply_rope(x, freqs):
# x: [batch, seq_len, n_heads, head_dim]
# freqs: [seq_len, head_dim // 2]
# 把实数向量转成复数
x_complex = torch.view_as_complex(x.reshape(*x.shape[:-1], -1, 2))
# 频率转成复数形式 e^(i * theta)
freqs_complex = torch.polar(torch.ones_like(freqs), freqs)
# 复数乘法 = 旋转
x_rotated = x_complex * freqs_complex
# 转回实数
return torch.view_as_real(x_rotated).flatten(-2)复数乘法 (a + bi) * (c + di) 等价于 2D 旋转,但计算更高效。
25.7.2 ALiBi 的实现
def alibi_bias(n_heads, seq_len):
# 每个头的斜率
slopes = 2 ** (-8 / n_heads * torch.arange(1, n_heads + 1))
# 距离矩阵
positions = torch.arange(seq_len)
distances = positions.unsqueeze(0) - positions.unsqueeze(1) # [seq, seq]
# 偏置 = 斜率 * 距离
bias = slopes.view(-1, 1, 1) * distances.unsqueeze(0) # [heads, seq, seq]
return bias就这么简单。
25.8 本章要点回顾
25.8.1 核心概念
| 概念 | 解释 |
|---|---|
| RoPE | 用旋转矩阵编码位置,相对位置自然涌现 |
| ALiBi | 在注意力分数上加线性距离惩罚 |
| YaRN | RoPE 的扩展,支持超长上下文 |
| 绝对位置 vs 相对位置 | Sinusoidal 是绝对的,RoPE/ALiBi 是相对的 |
| 外推能力 | 推理长度超过训练长度时的性能保持 |
25.8.2 技术演进脉络
2017: Sinusoidal (原始 Transformer)
|
| 问题:绝对位置,外推差
v
2021: RoPE (苏剑林)
|
| 问题:超长上下文
v
2021: ALiBi (Press et al.)
|
| 简洁但粗暴
v
2023: YaRN (扩展 RoPE)
|
| 支持 100k+ 上下文
v
未来: ?25.8.3 核心认知
位置编码的本质是让模型理解"谁在谁前面"。Sinusoidal 用加法告诉模型绝对位置,RoPE 用旋转让相对位置自然涌现,ALiBi 用惩罚让远距离 token 说话声音变小。没有完美的方案,只有合适的选择。
本章交付物
学完这一章,你应该能够:
- 解释 Sinusoidal 位置编码的局限性
- 用几何直觉理解 RoPE 的旋转思想
- 说明 RoPE 如何自然编码相对位置
- 理解 ALiBi 的线性惩罚机制
- 解释为什么 ALiBi 外推能力强
- 理解 YaRN 如何扩展上下文长度
- 为不同场景选择合适的位置编码方案
延伸阅读
- RoPE 原始论文:RoFormer: Enhanced Transformer with Rotary Position Embedding (Su et al., 2021)
- ALiBi 论文:Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation (Press et al., 2021)
- YaRN 论文:YaRN: Efficient Context Window Extension of Large Language Models (Peng et al., 2023)
- 苏剑林博客:关于 RoPE 的系列文章,提供了详细的数学推导
下一章预告
位置编码让模型知道"谁在谁前面"。下一章,我们将进入部署与微调的世界,学习如何用 LoRA/QLoRA 高效微调大模型,以及各种量化技术如何让模型跑在消费级硬件上。