一句话总结：矩阵乘法不只是数字运算，它的几何本质是"投影"——把一个向量投射到另一个向量上。理解这一点，是理解 Attention 机制的关键。

8.1 为什么要学矩阵？

在进入 Attention 机制之前，我们需要先搞清楚一个数学基础：矩阵乘法。

你可能会问：我又不是要当数学家，为什么要学这个？

答案很简单：Transformer 里到处都是矩阵乘法。

看这张图，Transformer 的核心概念：

3分钟秒懂矩阵相乘
注意力机制的几何逻辑
LayerNorm 就是数字缩放
FeedForward = 前馈网络 = 1行代码
Softmax 就是变数字为百分比
大模型参数(权重)在哪里？
最后到底咋预测的下一个字的概率

矩阵相乘排在第一位，因为它是理解后面所有内容的基础。

这一章，我们会用最直观的方式，让你"看懂"矩阵乘法在做什么。

8.2 基础概念：标量、向量、矩阵

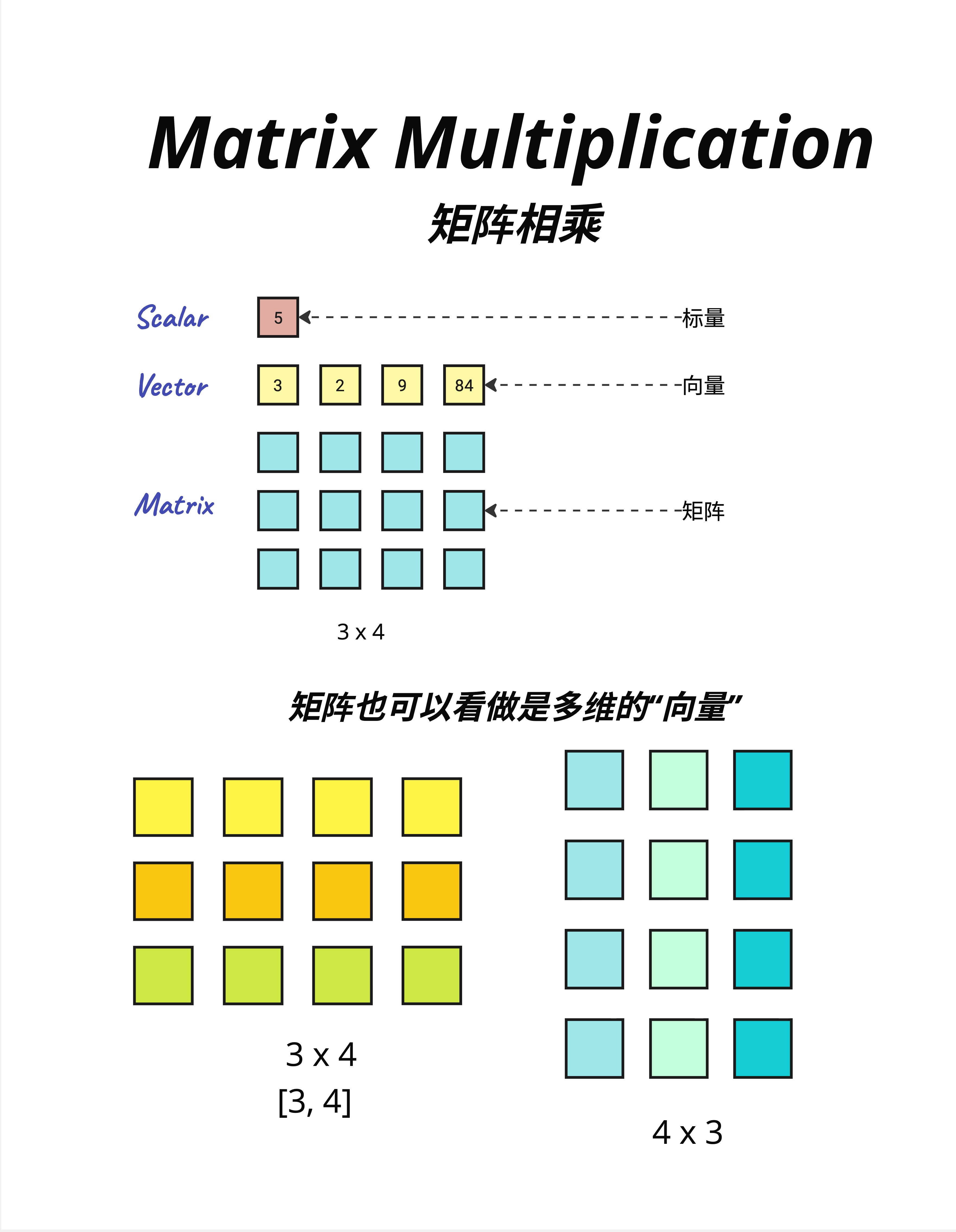
在开始之前，让我们统一一下术语。

8.2.1 标量（Scalar）

标量就是一个数字。

就这么简单。温度、价格、年龄，都是标量。

8.2.2 向量（Vector）

向量是一组有序的数字。

[3, 2, 9, 84]

向量可以表示很多东西：

位置：[x, y, z] = [3, 5, 2]
颜色：[R, G, B] = [255, 128, 0]
词向量：一个词的语义表示

8.2.3 矩阵（Matrix）

矩阵是二维的数字表格。

3 × 4 的矩阵：
┌─────────────┐
│ □ □ □ □ │
│ □ □ □ □ │
│ □ □ □ □ │
└─────────────┘

矩阵可以看作是"多个向量的堆叠"：

3×4 的矩阵 = 3 个长度为 4 的行向量
或者 = 4 个长度为 3 的列向量

8.2.4 在 Transformer 中

标量：学习率、温度参数
向量：一个 token 的 embedding
矩阵：一批 token 的 embedding、权重矩阵

8.3 矩阵乘法：计算过程

8.3.1 维度规则

矩阵乘法的维度规则：

[A, B] × [B, C] = [A, C]

中间的维度必须相同（都是 B），结果取两边的维度。

8.3.2 手算示例

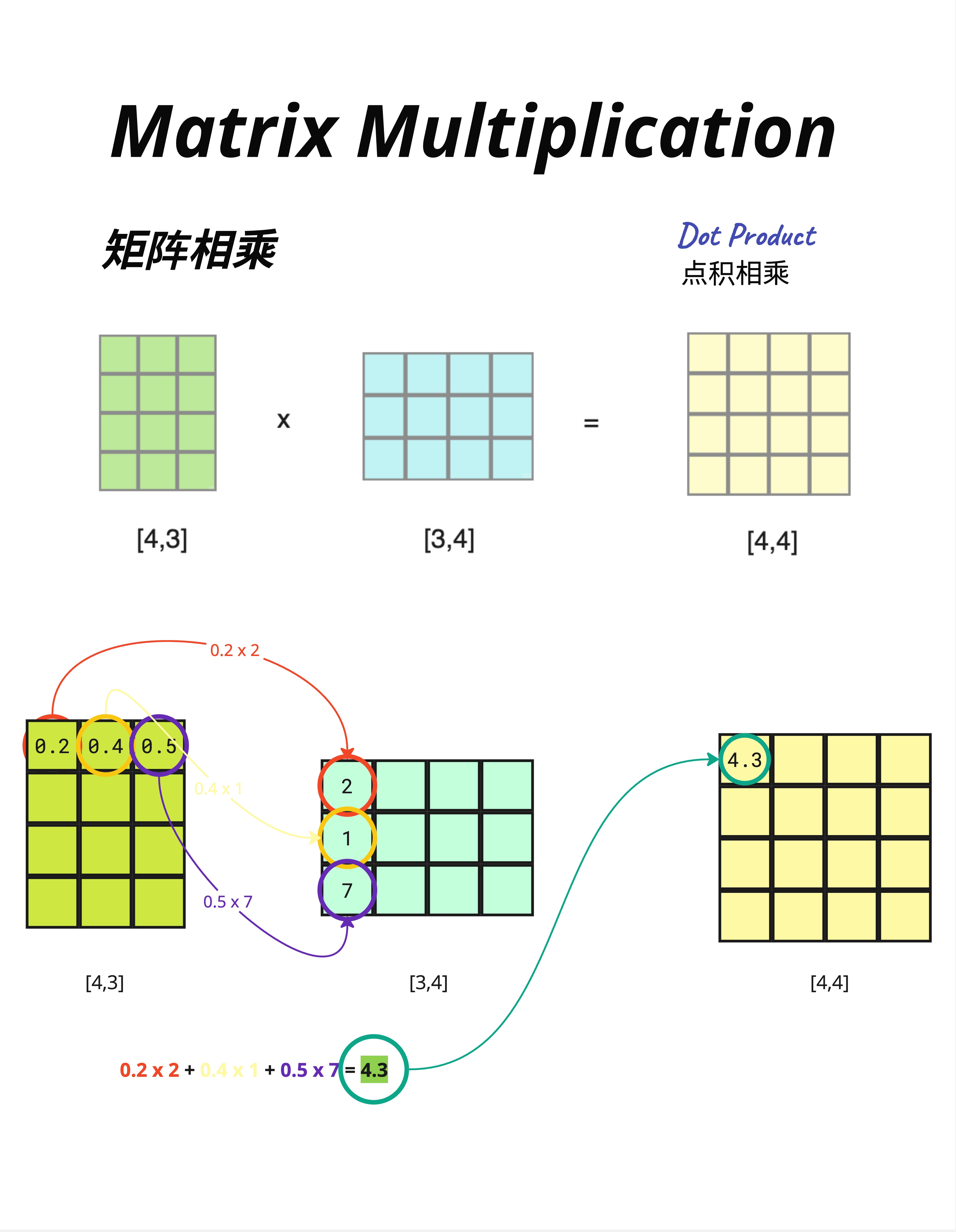
让我们看一个具体例子：

[4,3] × [3,4] = [4,4]

计算过程（以结果矩阵的第一个元素 4.3 为例）：

第一行 × 第一列：
[0.2, 0.4, 0.5] · [2, 1, 7]ᵀ
= 0.2×2 + 0.4×1 + 0.5×7
= 0.4 + 0.4 + 3.5
= 4.3

核心操作就是"点积"（Dot Product）：对应位置相乘，然后求和。

8.3.3 为什么叫"点积"？

因为数学上用一个点（·）来表示这个操作：

A · B = a₁b₁ + a₂b₂ + a₃b₃ + ...

在 Python/NumPy 中用 @ 符号：

C = A @ B  # 矩阵乘法

8.4 矩阵乘法 vs 线性变换

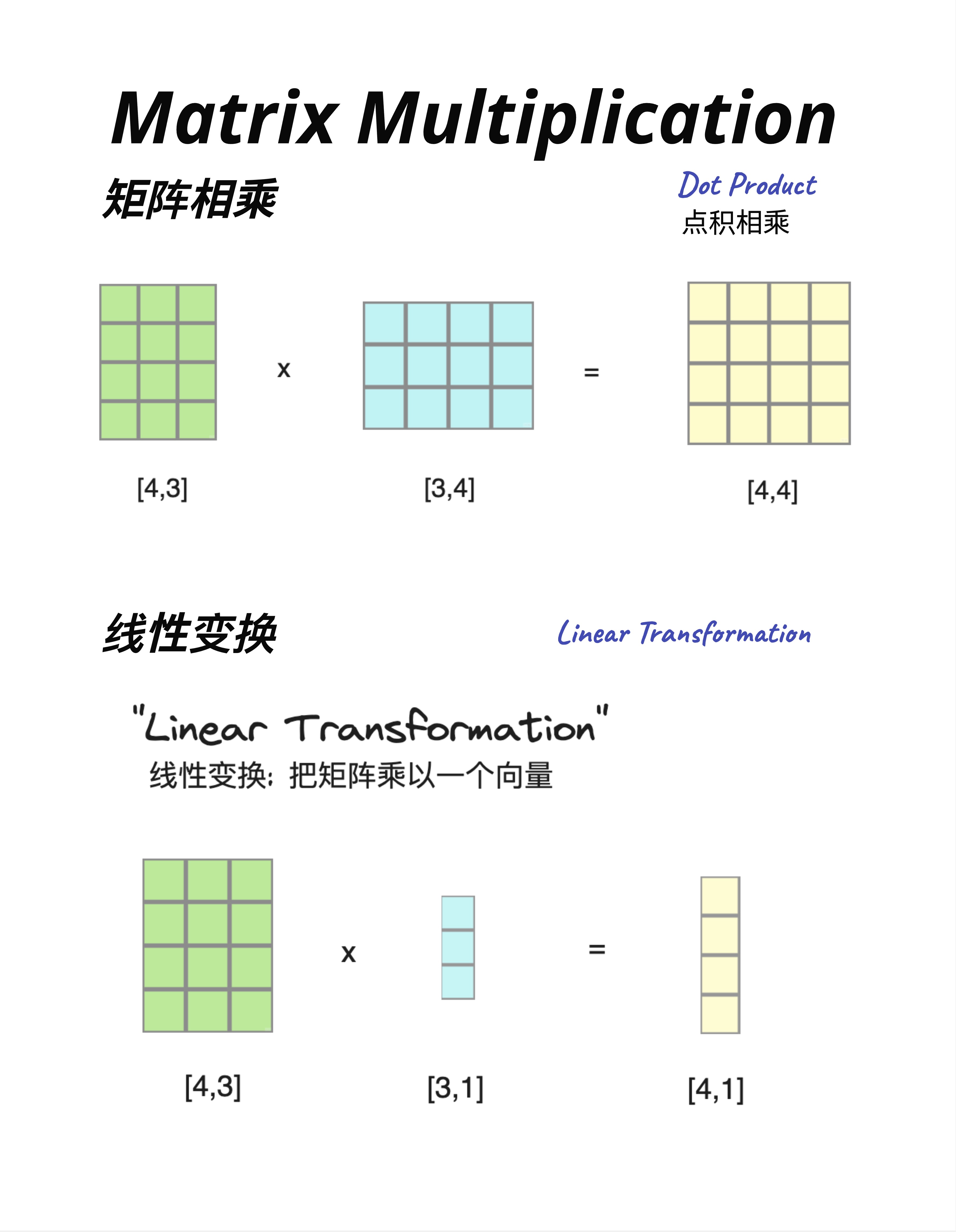
8.4.1 两种视角

同样的矩阵乘法，可以从两个角度理解：

视角一：矩阵相乘（Dot Product）

[4,3] × [3,4] = [4,4]

两个矩阵相乘，得到一个新矩阵。

视角二：线性变换（Linear Transformation）

[4,3] × [3,1] = [4,1]

用一个矩阵"变换"一个向量，得到一个新向量。

8.4.2 线性变换的直觉

"线性变换"这个名字听起来很数学，但本质很简单：

用矩阵乘以向量，把向量从一个空间"变换"到另一个空间。

比如：

输入：3 维向量
权重矩阵：[4,3]
输出：4 维向量

向量的维度从 3 变成了 4——这就是"变换"。

在 Transformer 中：

Embedding 把 token ID 变换成 d_model 维向量
Attention 的 Wq、Wk、Wv 把向量变换到不同的"空间"
FFN 把向量变换到更高维再变回来

到处都是线性变换！

8.5 几何意义：向量空间可视化

现在让我们进入最精彩的部分——理解矩阵乘法的几何意义。

8.5.1 词向量的3D可视化

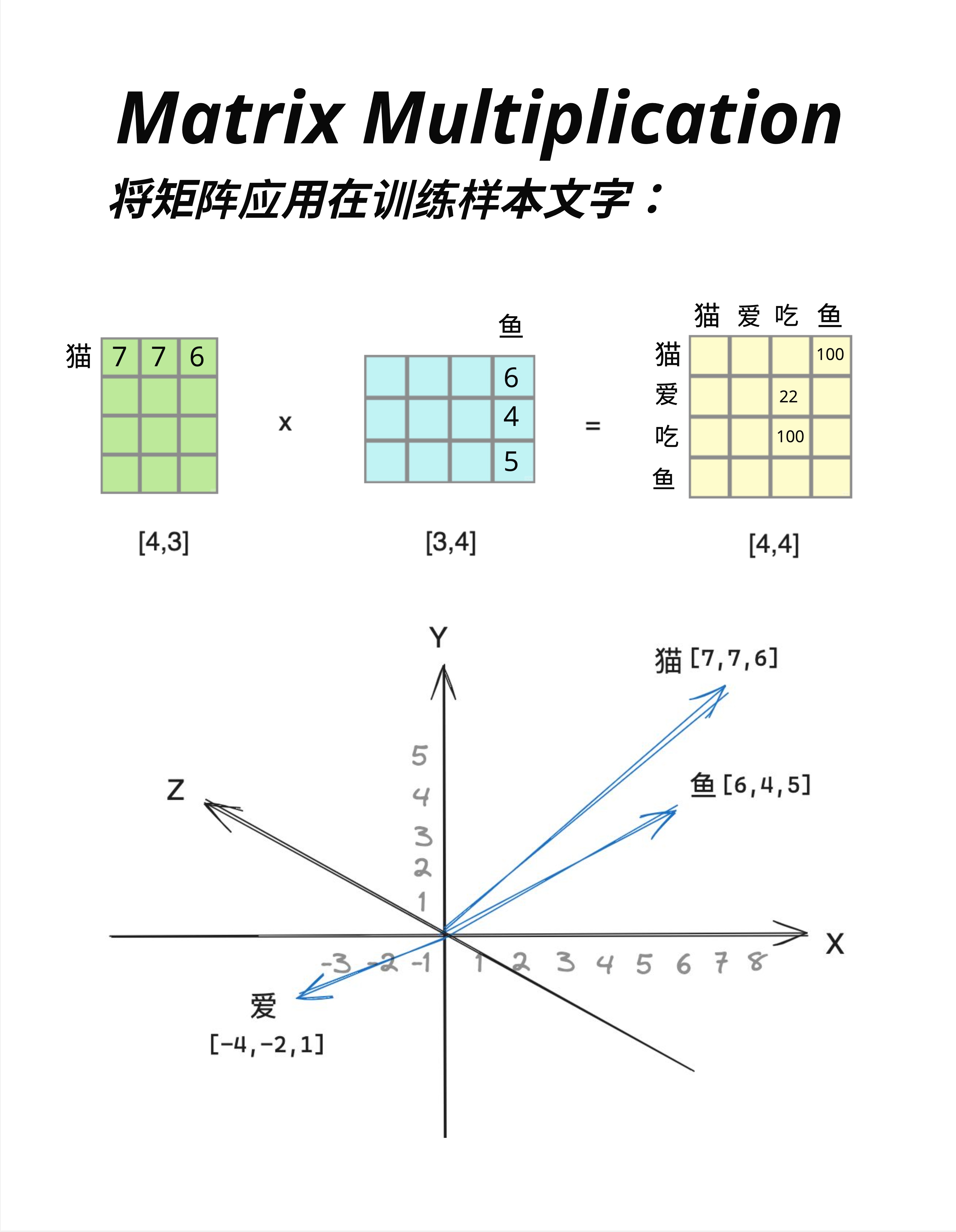
假设我们有一个简化的词向量空间，每个词用 3 维向量表示：

猫 = [7, 7, 6]
鱼 = [6, 4, 5]
爱 = [-4, -2, 1]

把它们画在 3D 坐标系中：

猫和鱼的向量方向相近（都在第一象限）
爱的向量指向完全不同的方向

这反映了语义关系：猫和鱼（名词、具体事物）比较相近，而爱（动词、抽象概念）很不同。

8.5.2 矩阵乘法生成相似度矩阵

看图中上方的矩阵乘法：

词向量矩阵 [4,3] × 鱼向量 [3,4] = 相似度矩阵 [4,4]

结果矩阵的每个元素，表示两个词的"相似程度"：

猫-鱼：100（很相似）
爱-鱼：22（不太相似）
吃-鱼：100（很相似，因为猫爱吃鱼！）

矩阵乘法天然就能计算"相似度"！ 这就是为什么 Attention 机制用矩阵乘法来计算注意力权重。

8.5.3 d_model 的含义

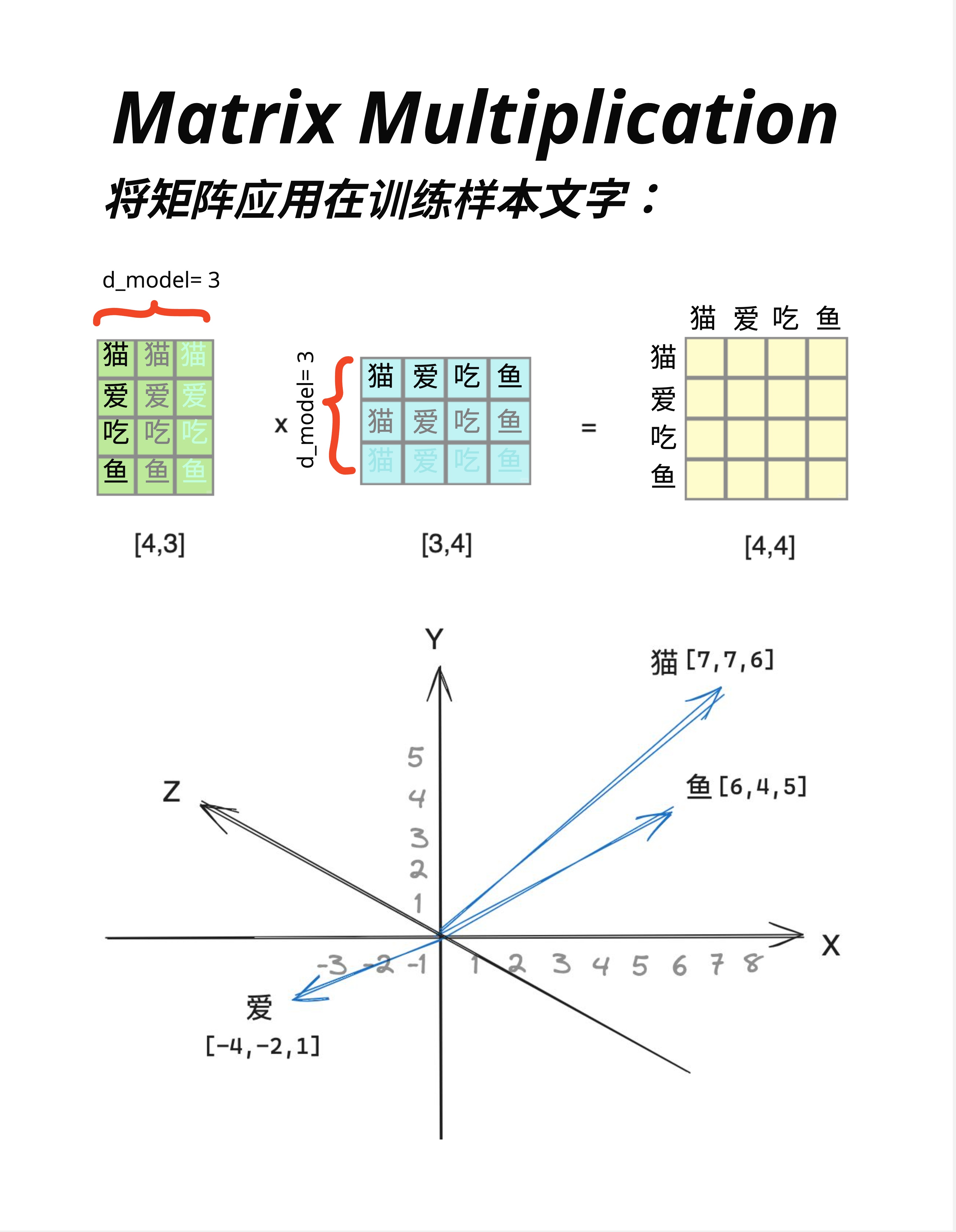
在这张图中，我们标注了 d_model = 3：

每个词用 3 维向量表示
矩阵的列数 = d_model

在真实的 Transformer 中：

GPT-2 Small：d_model = 768
GPT-3：d_model = 12288
LLaMA-7B：d_model = 4096

维度越高，表达能力越强，但计算量也越大。

8.6 点积的几何解释：余弦相似度

8.6.1 两个向量的夹角

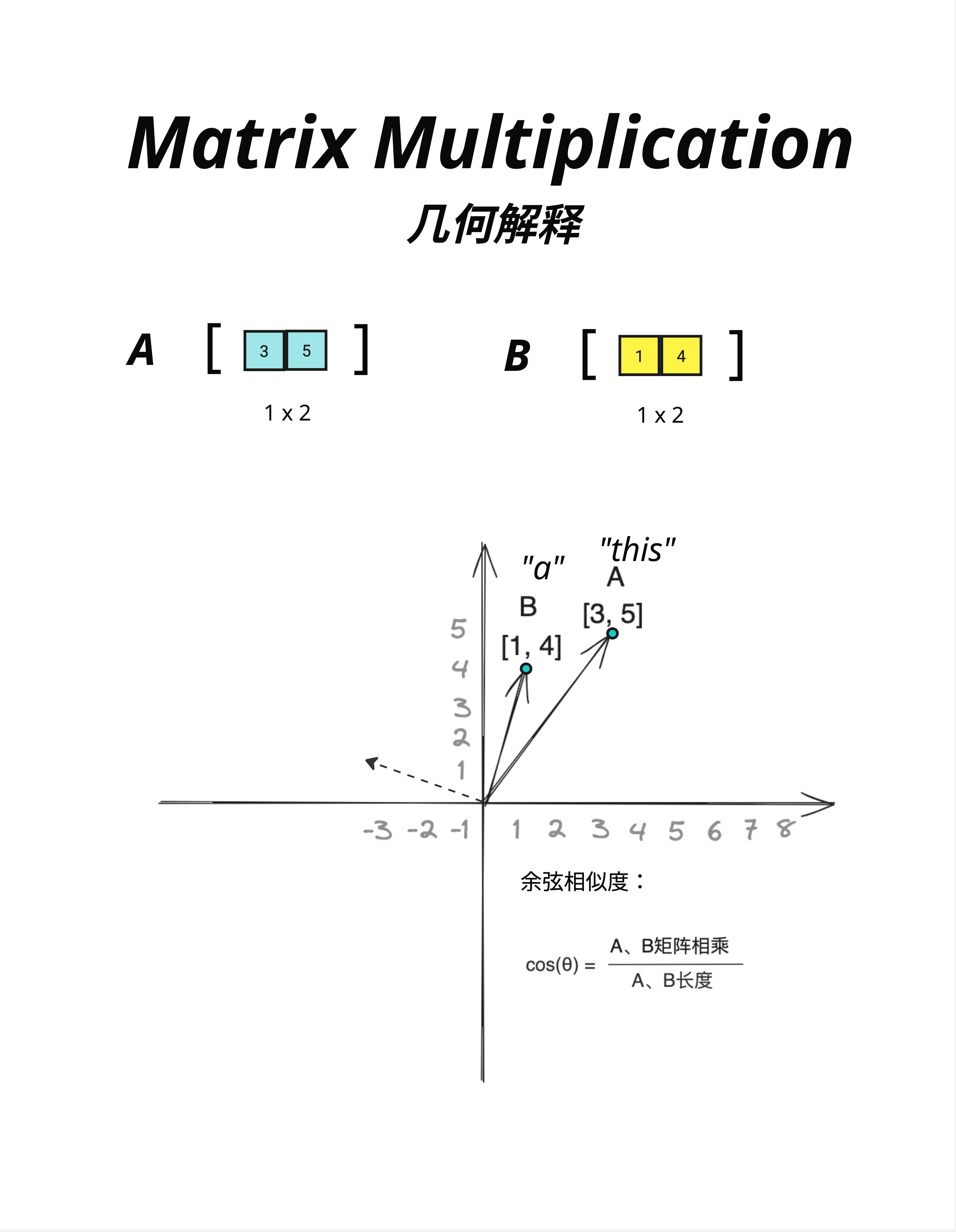
当两个向量做点积时，结果和它们的夹角有关：

cos(θ) = (A · B) / (|A| × |B|)

也就是说：

A · B = |A| × |B| × cos(θ)

其中：

|A| 是向量 A 的长度
|B| 是向量 B 的长度
θ 是两个向量的夹角

8.6.2 几何直觉

看图中的例子：

A = "this" = [3, 5]
B = "a" = [1, 4]

两个向量在 2D 平面上，它们之间有一个夹角 θ。

夹角小（cos(θ) 接近 1）→ 点积大 → 很相似
夹角大（cos(θ) 接近 0）→ 点积小 → 不太相似
垂直（cos(θ) = 0）→ 点积为 0 → 完全不相关
相反方向（cos(θ) = -1）→ 点积为负 → 相反/对立

8.6.3 这就是 Attention 的核心！

在 Attention 机制中：

Query 向量和 Key 向量做点积
点积越大，说明它们越"相似"
越相似的位置，获得越高的注意力权重

Attention 本质上就是在用点积计算"相似度"！

8.7 投影：另一种几何解释

8.7.1 投影的概念

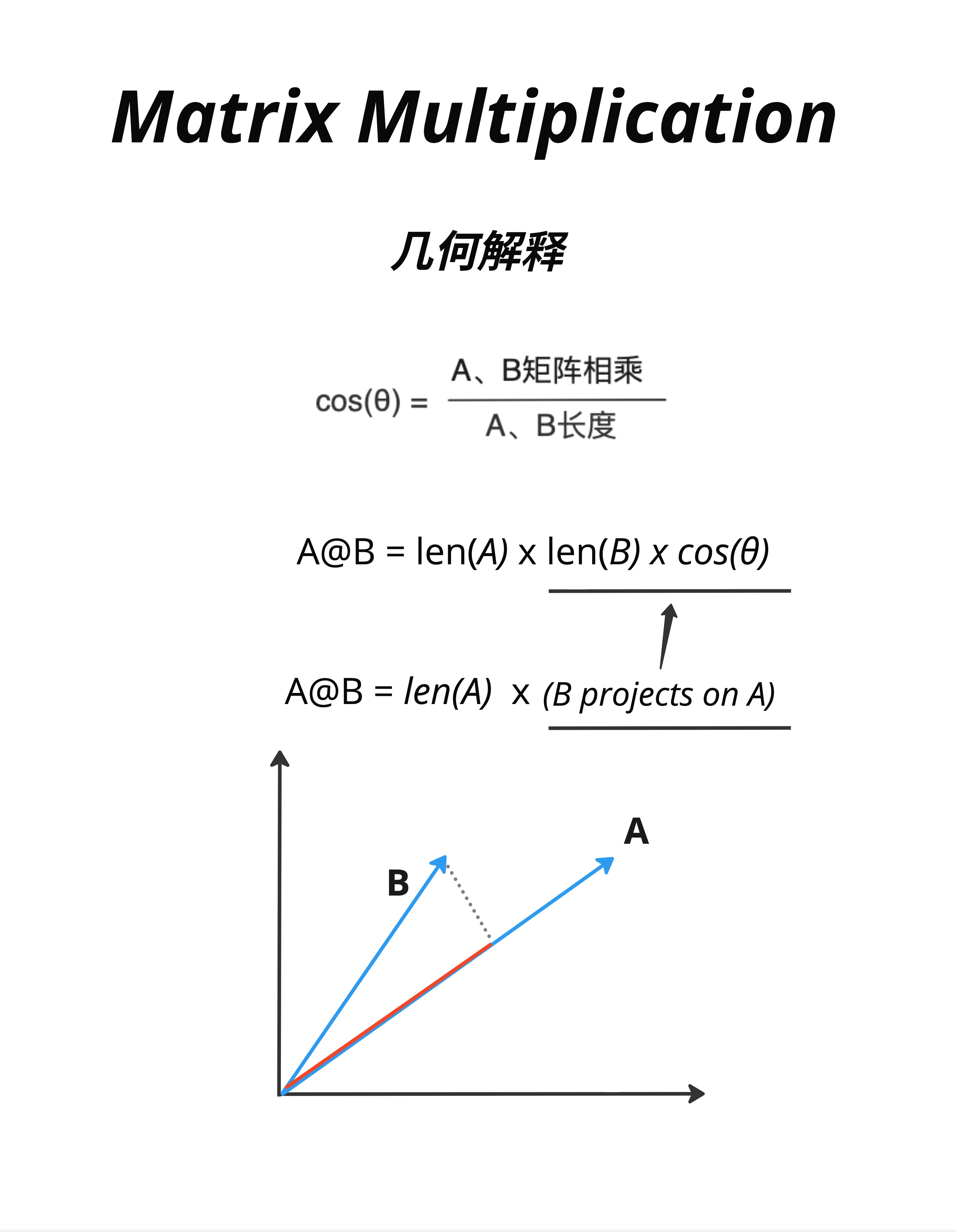
点积还有另一种几何解释：投影。

A @ B = |A| × (B 在 A 方向上的投影长度)

或者写成：

A @ B = len(A) × (B projects on A)

8.7.2 可视化

看图中的示意：

向量 A（红色）
向量 B（蓝色）
B 在 A 方向上的投影（虚线）

点积的结果 = A 的长度 × 投影的长度

8.7.3 投影的直觉

"投影"可以理解为："B 有多少成分在 A 的方向上"。

在 NLP 中：

如果"国王"和"皇室"的投影很大，说明它们在"皇室"这个维度上很相关
如果"国王"和"苹果"的投影很小，说明它们没什么关系

8.8 总结：为什么这对 Attention 很重要

8.8.1 Attention 的核心计算

Attention 的公式：

Attention(Q, K, V) = softmax(QKᵀ / √d) × V

其中 QKᵀ 就是 Query 和 Key 的矩阵乘法。

现在你知道了：

这个矩阵乘法计算的是 Query 和 Key 的相似度
相似度高的位置会获得更高的注意力权重
几何上，这是在计算两个向量的夹角余弦或投影

8.8.2 核心洞察

数学操作	几何意义	在 Attention 中的作用
点积 A·B	相似度 / 投影	计算 Q 和 K 的相关程度
矩阵乘法	批量点积	一次计算所有位置的相似度
Softmax	归一化	把相似度变成概率分布

8.8.3 记住这句话

矩阵乘法的几何本质是"投影"——计算一个向量在另一个向量方向上有多少成分。Attention 就是利用这个原理，找出哪些位置和当前位置最"相关"。

8.9 本章总结

8.9.1 核心概念

概念	解释
标量	单个数字
向量	一组有序的数字
矩阵	二维数字表格
点积	对应相乘再求和
线性变换	用矩阵变换向量的维度
余弦相似度	两向量夹角的余弦值
投影	一个向量在另一个方向上的分量

8.9.2 关键公式

点积：

A · B = a₁b₁ + a₂b₂ + ... + aₙbₙ

余弦相似度：

cos(θ) = (A · B) / (|A| × |B|)

投影：

A · B = |A| × |B| × cos(θ)

8.9.3 核心认知

矩阵乘法不是抽象的数学运算，它有直观的几何意义：计算相似度、做投影。理解这一点，Attention 机制就不再神秘了——它就是在用矩阵乘法找"相关的内容"。

本章交付物

学完这一章，你应该能够：

说出矩阵乘法的维度规则 [A,B] × [B,C] = [A,C]
手算简单的点积（对应相乘再求和）
解释点积的几何意义（余弦相似度、投影）
理解为什么 Attention 用矩阵乘法计算相似度

下一章预告

有了矩阵乘法的几何直觉，下一章我们正式进入 Attention 机制。

我们会回答这些问题：

为什么要用点积计算注意力？
Query、Key、Value 到底是什么？
Attention 的计算流程是怎样的？