English中文日本語

一句话总结：Multi-Head Attention 把 Attention 分成多个"头"，每个头关注不同的信息模式，就像用多双眼睛从不同角度观察同一个句子，最后把所有观察结果合并起来。

11.1 为什么需要多个头？

11.1.1 单头 Attention 的局限

在上一章，我们学习了 Attention 的完整计算流程。但那是单头 Attention——只有一组 Q、K、V。

单头 Attention 有一个问题：只能学习一种注意力模式。

但语言是多维度的！考虑这个句子：

"The cat sat on the mat because it was tired."

理解这个句子需要关注多种关系：

  • 语法关系：sat 的主语是 cat
  • 指代关系：it 指的是 cat
  • 位置关系：on the mat 是 sat 的地点
  • 因果关系：because 连接原因和结果

一个头很难同时捕捉所有这些关系。

11.1.2 解决方案：多个头

Multi-Head Attention 的核心思想：用多个 Attention 头，每个头学习不同的注意力模式。

Head 1：可能关注语法结构（主谓宾）
Head 2：可能关注指代关系（代词和名词）
Head 3：可能关注位置信息（相邻的词）
Head 4：可能关注语义相似性（同义词）
...

最后把所有头的结果合并，得到更丰富的表示。

11.1.3 一个形象的类比

想象你在分析一幅画：

  • 一双眼睛：只能关注一个方面（比如颜色）
  • 多双眼睛：同时关注颜色、形状、纹理、构图...

Multi-Head Attention 就像给模型配了多双眼睛，每双眼睛专注于不同的特征。

11.2 切分多头：把 d_model 分成 num_heads 份

11.2.1 维度切分

切分多头

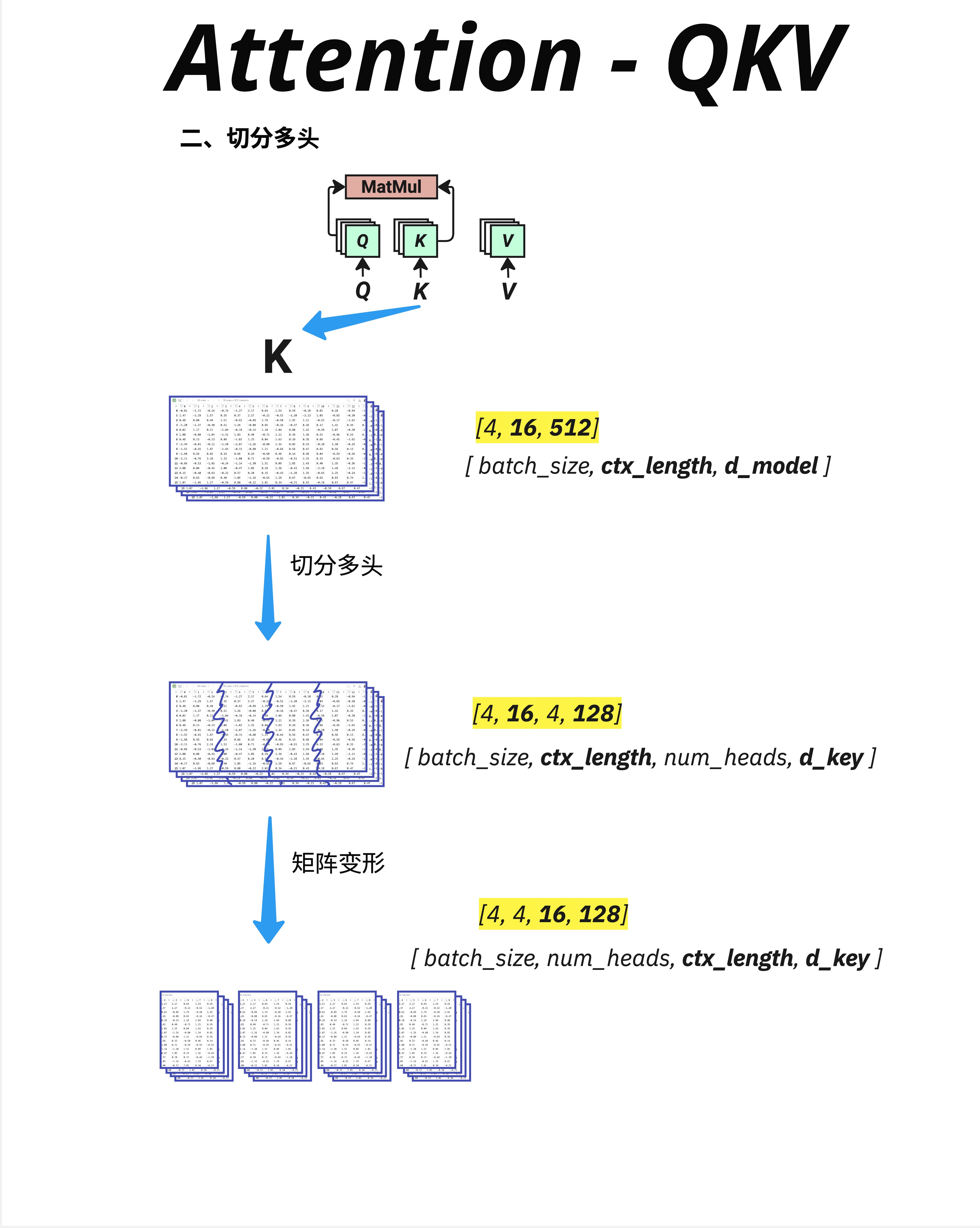
Multi-Head 的核心操作是切分维度。

以 K（Key）为例，假设：

  • d_model = 512
  • num_heads = 4
  • 则 d_key = d_model / num_heads = 512 / 4 = 128

切分过程：

原始 K: [batch_size, ctx_length, d_model]
      = [4, 16, 512]
              ↓
切分：  [batch_size, ctx_length, num_heads, d_key]
      = [4, 16, 4, 128]
              ↓
转置：  [batch_size, num_heads, ctx_length, d_key]
      = [4, 4, 16, 128]

11.2.2 为什么要转置？

转置是为了方便后续的矩阵运算。

转置后的形状 [batch, num_heads, seq_len, d_key] 可以理解为：

  • 对于每个 batch 中的样本
  • 有 num_heads 个独立的 Attention 头
  • 每个头处理 seq_len 个位置
  • 每个位置用 d_key 维向量表示

这样，每个头可以独立计算 Attention，互不干扰。

11.2.3 Q、K、V 都要切分

同样的切分操作应用于 Q、K、V：

Q: [4, 16, 512] → [4, 4, 16, 128]
K: [4, 16, 512] → [4, 4, 16, 128]
V: [4, 16, 512] → [4, 4, 16, 128]

现在我们有了 4 组 (Q, K, V)，可以进行 4 次独立的 Attention 计算。

11.2.4 两种切分实现方式

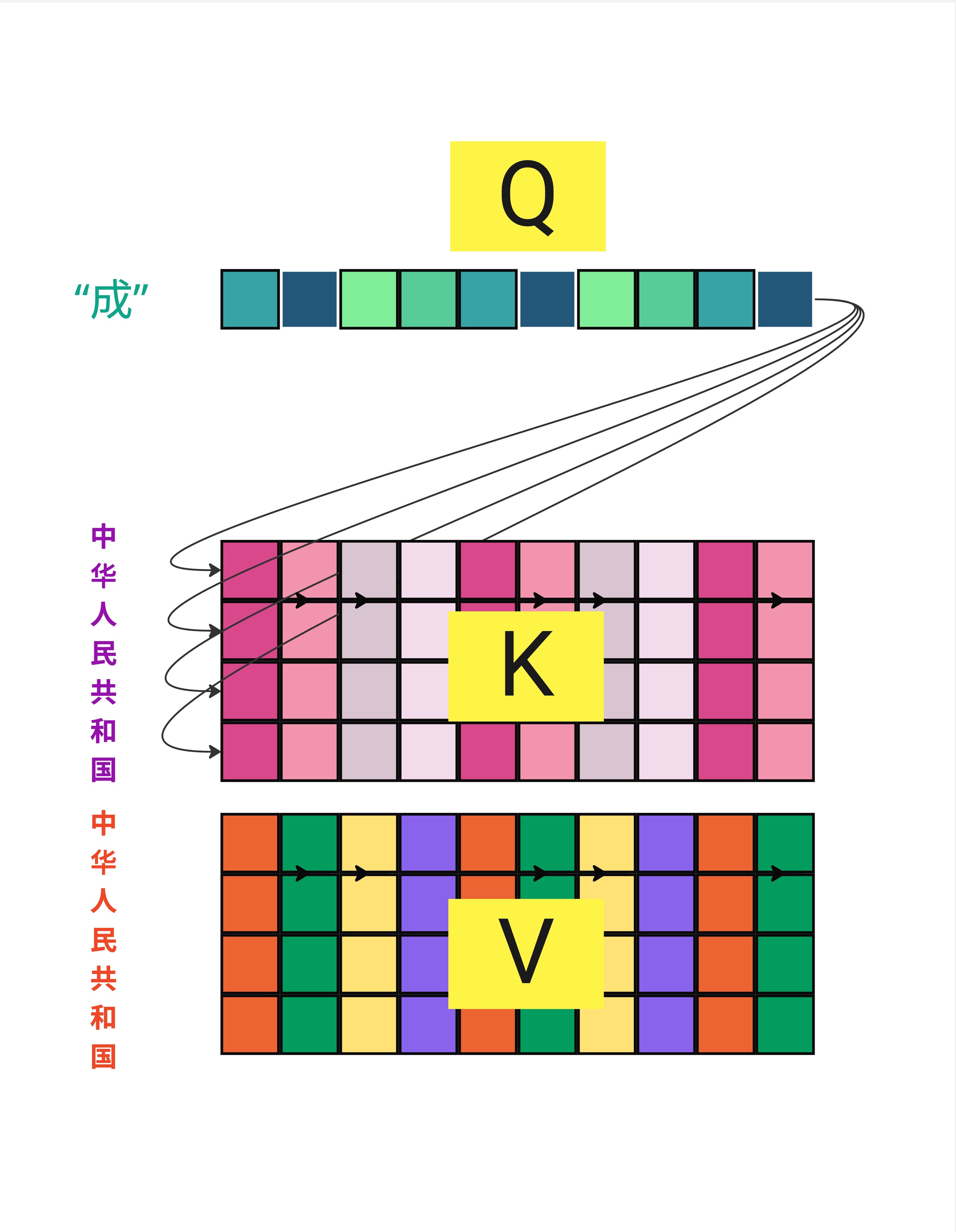
切分方式对比

实际上，Multi-Head 的"切分"有两种等价的实现方式：

方式一：在线性变换层进行多头"切分"（左图）

  • 概念上每个头有自己独立的 Wq、Wk、Wv 矩阵
  • 每个头独立计算 Q = X @ Wq_h
  • 这是概念理解的方式

方式二：在向量上砍 N 刀均分"切分"（右图）

  • 用一个大的 Wq 矩阵生成完整的 Q
  • 然后把 Q 沿着 d_model 维度切成 num_heads 份
  • 这是实际实现的方式（更高效）

两种方式数学上是等价的！实际代码中通常使用方式二，因为：

  • 一次大矩阵乘法比多次小矩阵乘法更高效
  • GPU 更擅长处理大的连续矩阵运算

11.3 并行计算多个头

11.3.1 每个头独立计算

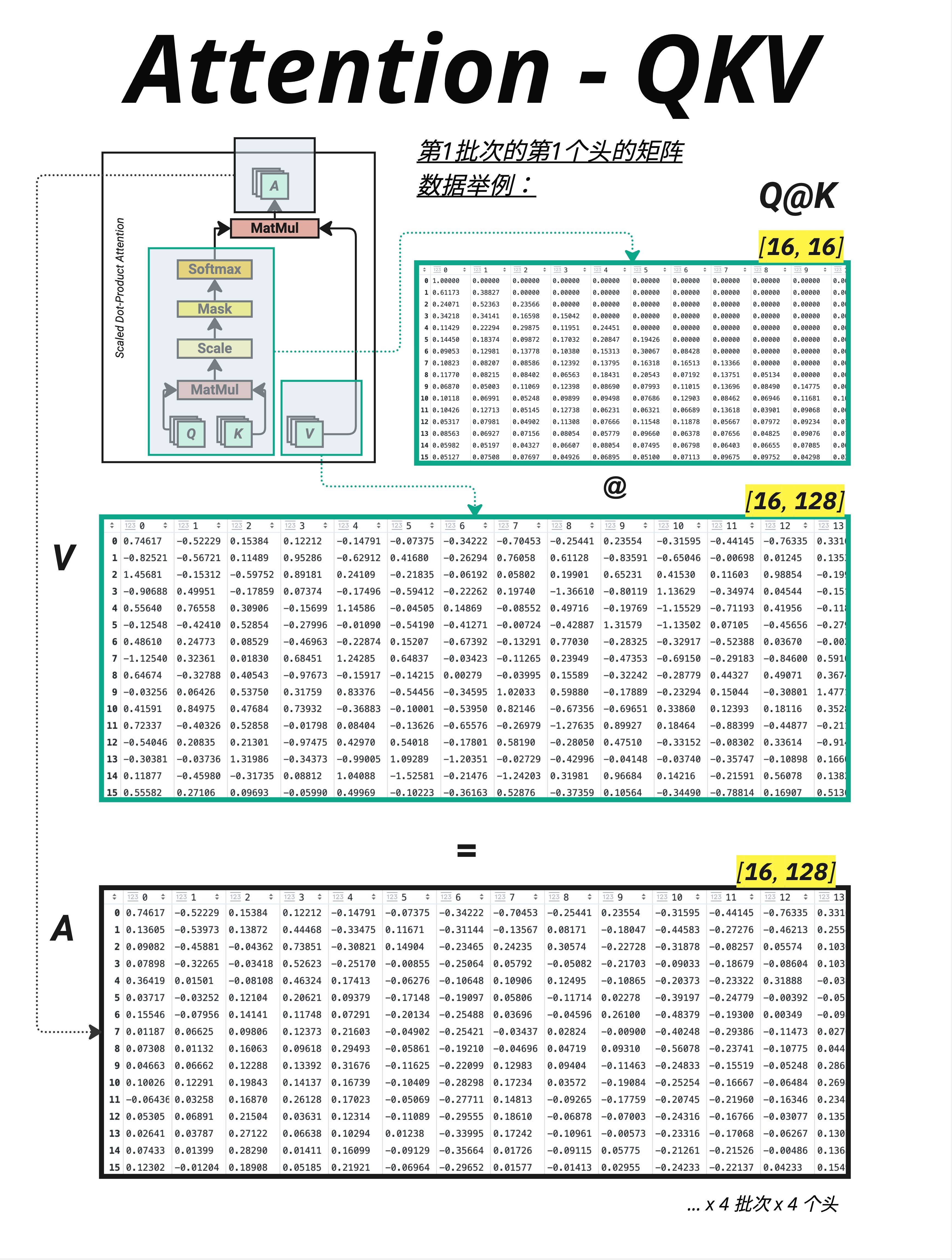
完整多头计算

切分后，每个头独立执行 Attention 计算：

对于每个 head h = 1, 2, 3, 4：
    scores_h = Q_h @ K_h^T   [4, 16, 128] @ [4, 128, 16] = [4, 16, 16]
    weights_h = softmax(scores_h / √d_key)
    output_h = weights_h @ V_h   [4, 16, 16] @ [4, 16, 128] = [4, 16, 128]

11.3.2 维度追踪

让我们详细追踪一次计算：

Q @ K^T：

Q: [4, 4, 16, 128]
   batch heads seq d_key

K^T: [4, 4, 128, 16]
     batch heads d_key seq

Q @ K^T: [4, 4, 16, 16]
         batch heads seq seq

Softmax(Q @ K^T) @ V：

Attention Weights: [4, 4, 16, 16]
                   batch heads seq seq

V: [4, 4, 16, 128]
   batch heads seq d_key

Output: [4, 4, 16, 128]
        batch heads seq d_key

11.3.3 图中的数据示例

图中展示了第 1 批次的第 1 个头：

  • Q @ K 结果是一个 [16, 16] 的注意力矩阵
  • 乘以 V [16, 128] 得到 [16, 128] 的输出
  • 这只是 4 个头中的一个！

11.4 合并多头输出

11.4.1 Concatenate：拼接所有头

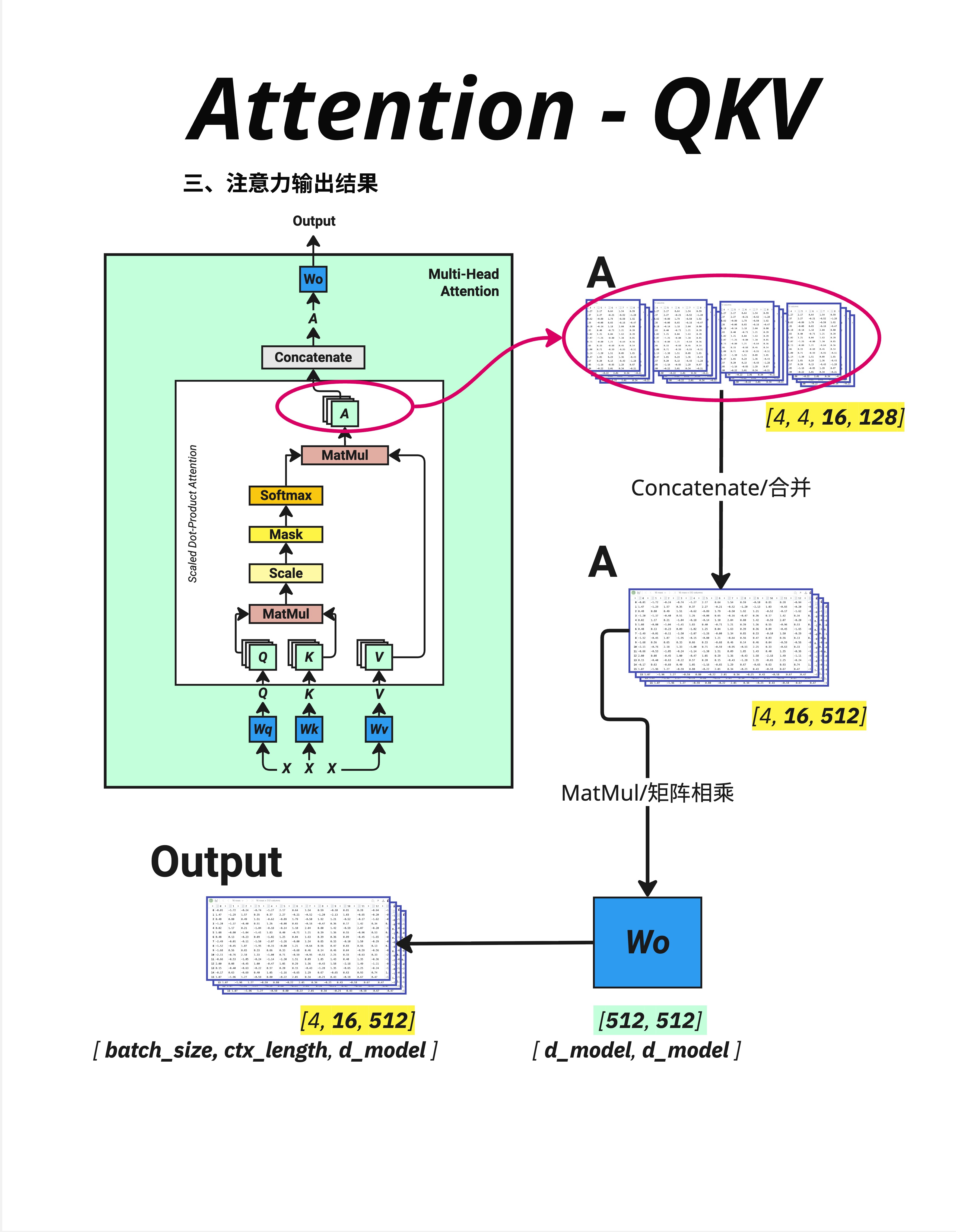
合并和Wo

计算完所有头后，需要把它们合并回去：

各头输出: [4, 4, 16, 128]
          batch heads seq d_key
              ↓
转置：     [4, 16, 4, 128]
          batch seq heads d_key
              ↓
合并：     [4, 16, 512]
          batch seq d_model

合并操作就是把最后两个维度"拼接"起来：

  • 4 个头 × 128 维 = 512 维

11.4.2 Wo：输出投影

合并后还有一个输出投影：

A @ Wo
[4, 16, 512] @ [512, 512] = [4, 16, 512]

Wo（Output Weight） 是一个可学习的矩阵，作用是：

  1. 融合不同头的信息
  2. 把拼接的表示转换到统一的空间
  3. 让模型学习如何组合各头的输出

11.4.3 为什么需要 Wo？

拼接后的向量是"机械地"把各头的输出放在一起，没有任何交互。

Wo 允许模型学习：

  • 哪些头的输出更重要
  • 不同头之间如何配合
  • 最终输出应该是什么样的

11.5 输出对比

11.5.1 A vs A @ Wo

输出对比

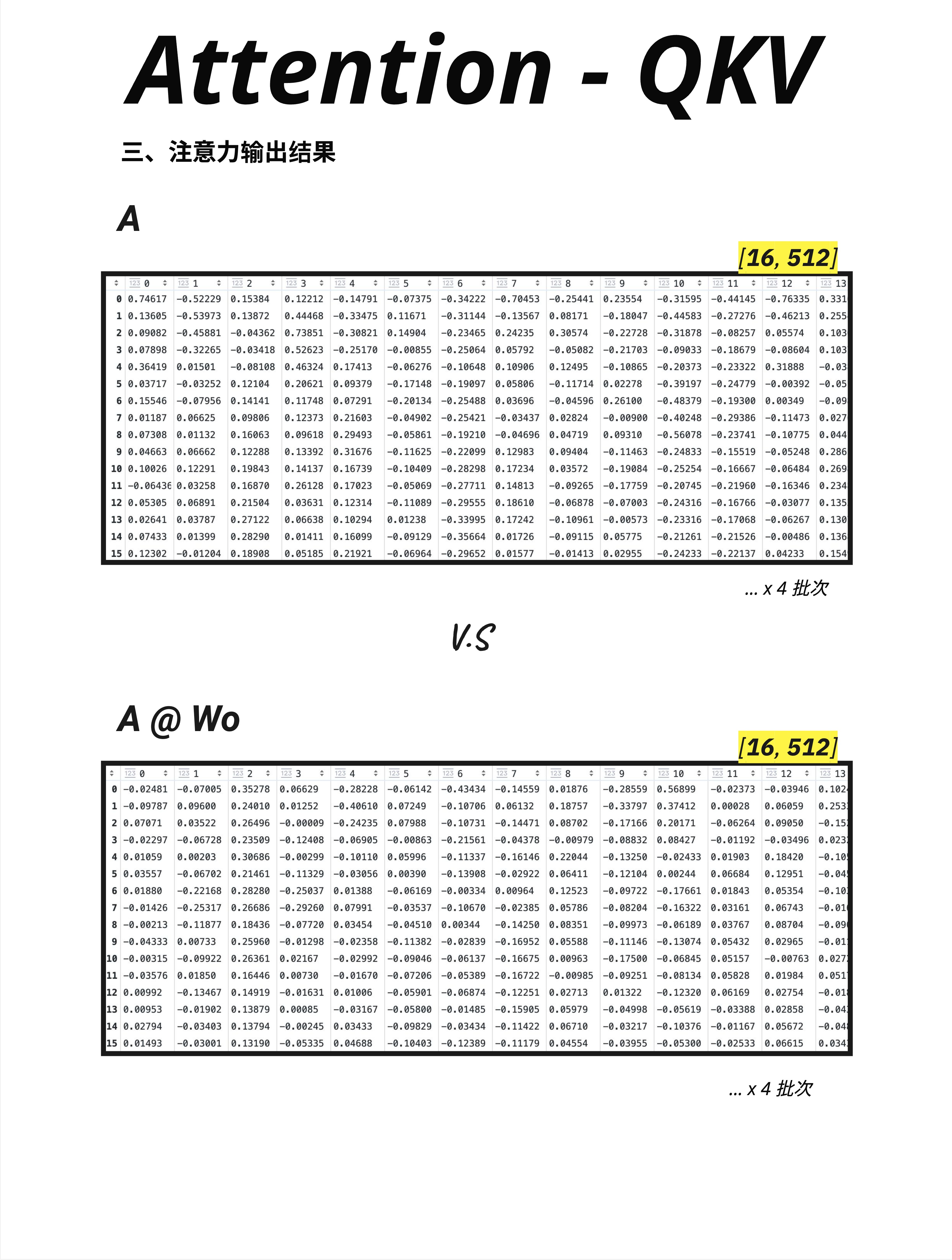
图中对比了两种输出：

上方（A）：合并后、Wo 之前的输出

  • 形状：[16, 512]
  • 是各头输出的简单拼接

下方（A @ Wo）：经过 Wo 投影后的最终输出

  • 形状：[16, 512]
  • 是经过混合和投影的结果

11.5.2 数值对比

虽然形状相同，但数值分布完全不同：

  • A 的数值是各头独立计算的结果
  • A @ Wo 的数值是所有头信息融合后的结果

这个最终输出会：

  1. 替代原始的 token embedding
  2. 进入下一层（LayerNorm → FFN）
  3. 或者作为下一个 Block 的输入

11.6 Multi-Head Attention 完整流程

11.6.1 流程图

输入 X [batch, seq, d_model]
        ↓
   生成 Q, K, V（通过 Wq, Wk, Wv）
        ↓
   切分多头 [batch, num_heads, seq, d_key]
        ↓
   并行计算 Attention（每个头独立）
        ↓
   合并多头 [batch, seq, d_model]
        ↓
   输出投影（@ Wo）
        ↓
输出 [batch, seq, d_model]

11.6.2 PyTorch 代码

# 代码示例
import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_key = d_model // num_heads

        # 四个可学习的权重矩阵
        self.Wq = nn.Linear(d_model, d_model)
        self.Wk = nn.Linear(d_model, d_model)
        self.Wv = nn.Linear(d_model, d_model)
        self.Wo = nn.Linear(d_model, d_model)

    def forward(self, x, mask=None):
        batch_size, seq_len, _ = x.shape

        # 1. 生成 Q, K, V
        Q = self.Wq(x)  # [batch, seq, d_model]
        K = self.Wk(x)
        V = self.Wv(x)

        # 2. 切分多头
        Q = Q.view(batch_size, seq_len, self.num_heads, self.d_key)
        K = K.view(batch_size, seq_len, self.num_heads, self.d_key)
        V = V.view(batch_size, seq_len, self.num_heads, self.d_key)

        # 转置: [batch, num_heads, seq, d_key]
        Q = Q.transpose(1, 2)
        K = K.transpose(1, 2)
        V = V.transpose(1, 2)

        # 3. 计算 Attention
        scores = torch.matmul(Q, K.transpose(-2, -1)) / (self.d_key ** 0.5)

        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))

        attention_weights = F.softmax(scores, dim=-1)
        attention_output = torch.matmul(attention_weights, V)

        # 4. 合并多头
        attention_output = attention_output.transpose(1, 2)  # [batch, seq, heads, d_key]
        attention_output = attention_output.contiguous().view(
            batch_size, seq_len, self.d_model
        )

        # 5. 输出投影
        output = self.Wo(attention_output)

        return output

11.7 关键数字

11.7.1 参数量计算

Multi-Head Attention 有四个权重矩阵：

矩阵形状参数量
Wq[d_model, d_model]d_model²
Wk[d_model, d_model]d_model²
Wv[d_model, d_model]d_model²
Wo[d_model, d_model]d_model²

总参数量 = 4 × d_model²

以 GPT-2 Small 为例（d_model = 768）：

  • 每层 Attention 参数量 = 4 × 768² ≈ 236 万

11.7.2 常见配置

模型d_modelnum_headsd_key
GPT-2 Small7681264
GPT-2 Medium10241664
GPT-2 Large12802064
GPT-31228896128
LLaMA-7B409632128

有趣的观察：

  • d_key 通常是 64 或 128
  • 不同模型通过调整 num_heads 来增加总维度

11.8 多头的可视化理解

11.8.1 每个头关注什么？

研究发现，不同的头确实会学习到不同的注意力模式：

头的类型关注的模式例子
位置头固定相对位置总是关注前一个词
语法头主谓宾关系动词关注主语
语义头相似含义同义词互相关注
指代头代词解析it 关注它指代的名词
分隔头句子边界关注标点符号

11.8.2 注意力模式示例

假设句子是 "The cat sat on the mat"：

Head 1（位置头）：
"sat" 主要关注 "cat"（前一个实词）

Head 2（语法头）：
"sat" 主要关注 "cat"（主语）

Head 3（语义头）：
"cat" 和 "mat" 互相有些关注（都是名词、押韵）

Head 4（指代头）：
暂时不活跃（没有代词）

11.8.3 头的冗余性

实际上，并非所有头都同等重要。研究表明：

  • 有些头可以被"剪枝"掉，对性能影响很小
  • 有些头学到的模式是冗余的
  • 但保留更多头通常能提供更好的鲁棒性

11.9 Multi-Head vs Single-Head

11.9.1 计算量对比

假设 d_model = 512，num_heads = 8，d_key = 64：

单头（d_key = 512）：

  • Q @ K^T：[seq, 512] @ [512, seq] → O(seq² × 512)

多头（d_key = 64）：

  • 8 个头，每个：[seq, 64] @ [64, seq] → O(seq² × 64)
  • 总计：8 × O(seq² × 64) = O(seq² × 512)

计算量基本相同！

11.9.2 效果对比

虽然计算量相同，但 Multi-Head 通常效果更好：

  • 能捕捉更多样的注意力模式
  • 更容易训练（每个头的任务更简单）
  • 提供了一种"集成学习"的效果

11.9.3 为什么不用更多头？

增加头的数量意味着减小 d_key：

d_key = d_model / num_heads

如果 d_key 太小：

  • 每个头的表达能力下降
  • 可能无法捕捉复杂的模式

常见的 d_key 通常是 64 或 128，这是一个经验性的平衡点。

11.10 本章总结

11.10.1 核心概念

概念解释
Multi-Head把 Attention 分成多个头并行计算
num_heads头的数量
d_key每个头的维度 = d_model / num_heads
切分把 d_model 维度分成 num_heads 份
合并把所有头的输出拼接回 d_model
Wo输出投影矩阵，融合各头信息

11.10.2 维度变化

输入:     [batch, seq, d_model]
             ↓
切分:     [batch, num_heads, seq, d_key]
             ↓
Attention: [batch, num_heads, seq, d_key]
             ↓
合并:     [batch, seq, d_model]
             ↓
Wo 投影:  [batch, seq, d_model]

11.10.3 核心认知

Multi-Head Attention 是 Transformer 的核心创新之一。它把 Attention 分成多个头，每个头可以学习不同的注意力模式——有的关注语法，有的关注语义，有的关注位置。最后通过 Concatenate + Wo 把所有头的信息融合起来。这让模型能够从多个角度理解语言，比单头 Attention 更加强大。

本章交付物

学完这一章，你应该能够：

  • 解释为什么需要 Multi-Head Attention
  • 说出 d_key = d_model / num_heads 的关系
  • 理解切分和合并的维度变化
  • 知道 Wo 矩阵的作用（融合各头信息）
  • 解释不同头可能学习到的不同模式

Part 3 总结

恭喜你完成了 Part 3：Attention 机制！

让我们回顾这三章学到的内容：

章节主题核心内容
第 8 章线性变换矩阵乘法 = 投影/相似度计算
第 9 章Attention 几何逻辑用点积计算相似度，找相关的词
第 10 章QKVQ 查询、K 键、V 值的完整计算流程
第 11 章Multi-Head多个头从不同角度理解句子

Attention 公式（完整版）：

textMultiHead(Q,K,V)=textConcat(texthead1,...,textheadh)WO\\text{MultiHead}(Q, K, V) = \\text{Concat}(\\text{head}_1, ..., \\text{head}_h) W^O

其中：

textheadi=textAttention(QWiQ,KWiK,VWiV)\\text{head}_i = \\text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
textAttention(Q,K,V)=textsoftmaxleft(fracQKTsqrtdkright)V\\text{Attention}(Q, K, V) = \\text{softmax}\\left(\\frac{QK^T}{\\sqrt{d_k}}\\right)V

下一章预告

Part 4 将介绍 完整架构——把所有组件组装起来：

  • 第 13 章：残差连接与 Dropout
  • 第 14 章：词嵌入 + 位置信息的深层逻辑
  • 第 15 章：Transformer 完整前向传播
  • 第 16 章：训练 vs 推理的异同

我们将把前面学到的所有组件串起来，看看完整的 Transformer 是如何工作的！

引用本文 / Cite
Zhang, W. (2026). 第 11 章：Multi-Head Attention - 多视角理解. In Transformer 架构：从直觉到实现. https://waylandz.com/llm-transformer-book/第11章-Multi-Head-Attention-多视角理解
@incollection{zhang2026transformer_第11章_Multi_Head_Attention_多视角理解,
  author = {Zhang, Wayland},
  title = {第 11 章：Multi-Head Attention - 多视角理解},
  booktitle = {Transformer 架构：从直觉到实现},
  year = {2026},
  url = {https://waylandz.com/llm-transformer-book/第11章-Multi-Head-Attention-多视角理解}
}