一句话总结：训练时可以并行处理整个序列（因为知道所有答案），推理时必须一个词一个词生成（因为下一个词依赖上一个词的结果）。这种"自回归"的特性是 GPT 能够生成连贯文本的关键。

16.1 训练 vs 推理：核心区别

16.1.1 一句话对比

	训练（Training）	推理（Inference）
目的	学习参数	生成文本
输入	完整的文本	初始提示（prompt）
答案	已知（下一个词）	未知（需要预测）
处理方式	并行（一次处理整个序列）	串行（一个词一个词生成）
是否更新参数	是	否

16.1.2 为什么有这个区别？

训练时：

我们有完整的训练文本："小沈阳江西演唱会邀请了沈春阳"
知道每个位置的"正确答案"
可以一次性计算所有位置的损失

推理时：

我们只有开头："小沈阳江西演唱会邀请了"
不知道下一个词是什么
必须先预测一个词，才能预测下一个词

16.2 训练过程详解

16.2.1 Teacher Forcing

训练时使用一种叫 Teacher Forcing 的技术：

输入：小 沈 阳 江 西 演 唱 会 邀 请 了
目标：沈 阳 江 西 演 唱 会 邀 请 了 沈

输入是原文，目标是原文右移一位。

每个位置都在预测"下一个词"：

位置 0（"小"）→ 预测"沈"
位置 1（"沈"）→ 预测"阳"
...
位置 10（"了"）→ 预测"沈"

16.2.2 并行计算

因为我们知道所有的输入和目标，可以一次性计算：

# 训练代码示例
def train_step(model, input_ids, target_ids):
    # 前向传播（一次处理整个序列）
    logits = model(input_ids)  # [batch, seq_len, vocab_size]

    # 计算损失（所有位置一起）
    loss = F.cross_entropy(
        logits.view(-1, vocab_size),
        target_ids.view(-1)
    )

    # 反向传播
    loss.backward()
    optimizer.step()

一次前向传播就处理了整个序列！

16.2.3 Causal Mask 的作用

虽然训练时输入整个序列，但每个位置只能看到之前的词，不能看到之后的词。

这是通过 Causal Mask（因果掩码） 实现的：

位置 0 看到：[小, -, -, -, -, ...]
位置 1 看到：[小, 沈, -, -, -, ...]
位置 2 看到：[小, 沈, 阳, -, -, ...]
...

这模拟了推理时的情况：每个位置只能基于已知的前文来预测。

16.3 推理过程详解

16.3.1 自回归生成

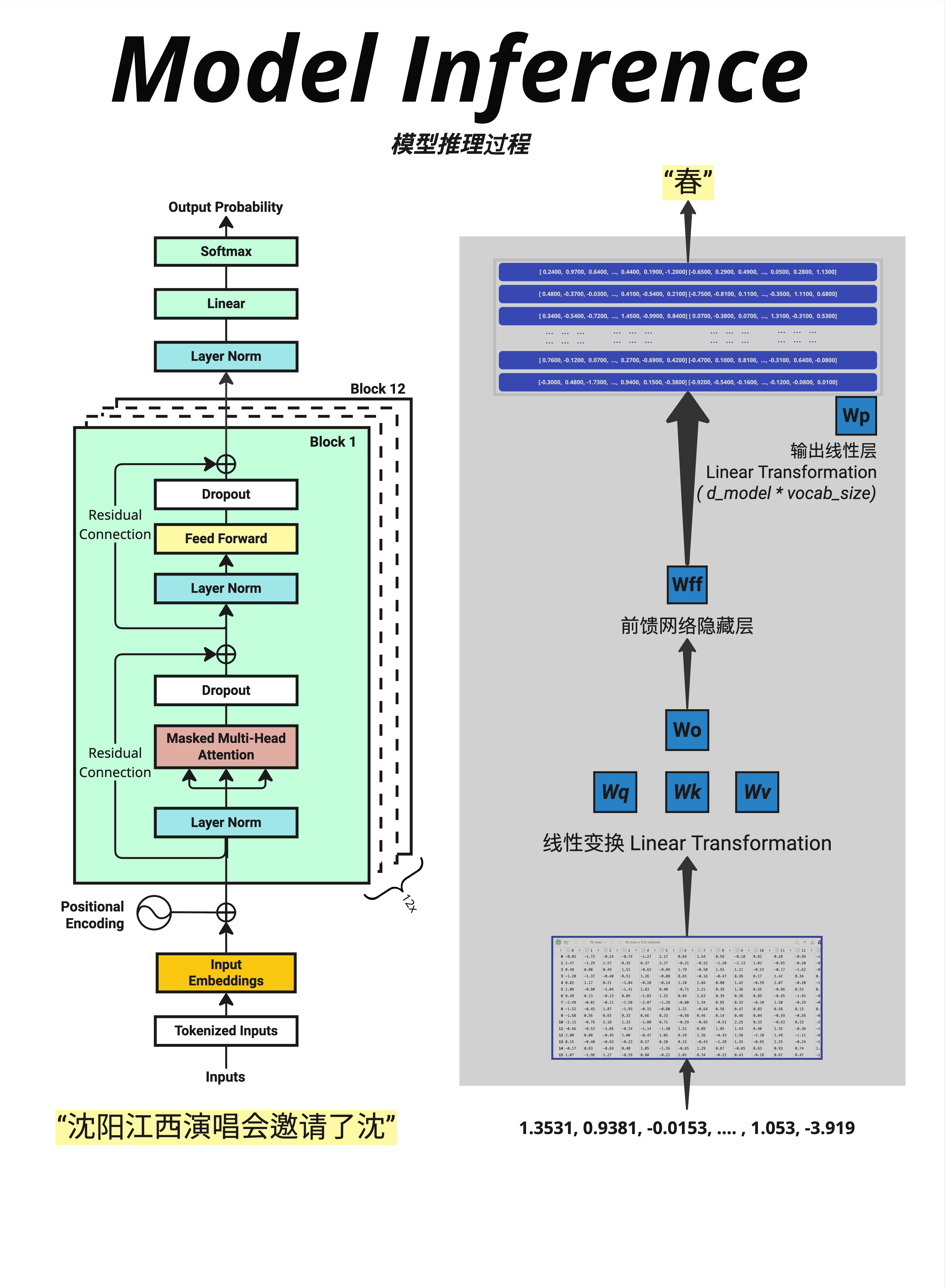
推理时，模型必须一个词一个词地生成：

输入："沈阳江西演唱会邀请了沈"
         ↓
      模型预测
         ↓
输出概率：[春=30%, 阳=25%, 的=10%, ...]
         ↓
      选择 "春"
         ↓
新输入："沈阳江西演唱会邀请了沈春"
         ↓
      模型预测
         ↓
输出概率：[阳=60%, 秋=15%, ...]
         ↓
      选择 "阳"

这叫做 自回归（Autoregressive） 生成：每一步的输出成为下一步的输入。

16.3.2 逐步生成示例

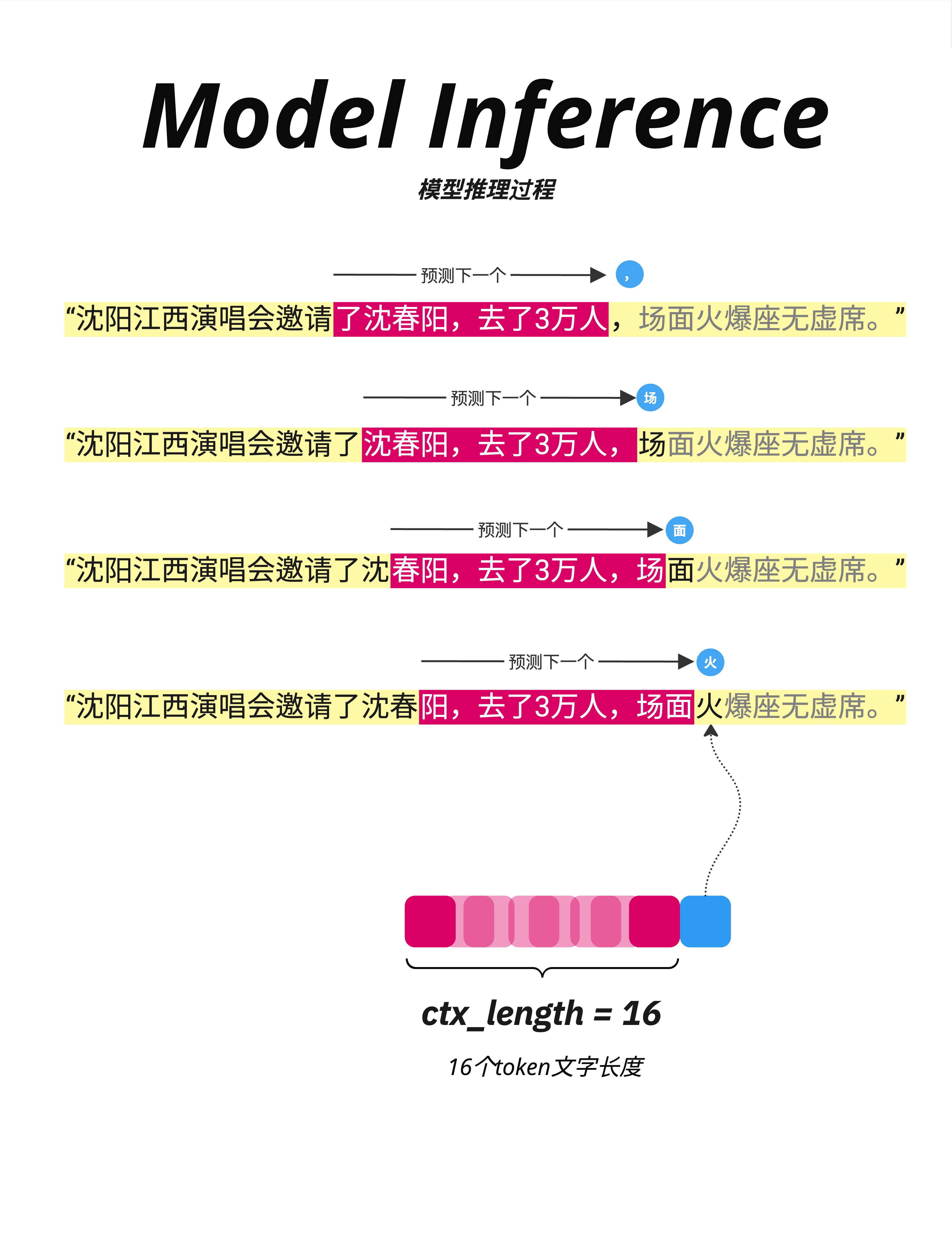
看这张图，展示了生成过程：

第 1 步：

输入："沈阳江西演唱会邀请了"
预测：","（逗号）

第 2 步：

输入："沈阳江西演唱会邀请了，"（加上逗号）
预测："沈"

第 3 步：

输入："沈阳江西演唱会邀请了，沈"
预测："春"

第 4 步：

输入："沈阳江西演唱会邀请了，沈春"
预测："阳"

以此类推，直到生成结束标记或达到最大长度。

16.3.3 Context Length 的滑动

图中下方展示了一个重要概念：ctx_length = 16

如果输入超过 16 个 token，需要使用滑动窗口：

保留最近的 16 个 token
丢弃更早的 token

这就是为什么 GPT 有"上下文长度限制"。

16.4 推理代码实现

16.4.1 基本推理循环

# 推理代码示例
def generate(model, prompt_ids, max_new_tokens=50):
    """
    自回归生成文本

    Args:
        model: GPT 模型
        prompt_ids: 初始 prompt 的 token IDs [1, seq_len]
        max_new_tokens: 最多生成多少个新 token
    """
    model.eval()  # 切换到推理模式（关闭 Dropout）

    generated = prompt_ids.clone()

    for _ in range(max_new_tokens):
        # 如果超过最大长度，截断
        input_ids = generated[:, -max_len:]

        # 前向传播
        with torch.no_grad():  # 不计算梯度
            logits = model(input_ids)

        # 只取最后一个位置的 logits
        next_token_logits = logits[:, -1, :]  # [1, vocab_size]

        # 选择下一个 token（这里用 greedy，取概率最高的）
        next_token = torch.argmax(next_token_logits, dim=-1, keepdim=True)

        # 拼接到已生成的序列
        generated = torch.cat([generated, next_token], dim=1)

        # 如果生成了结束标记，停止
        if next_token.item() == eos_token_id:
            break

    return generated

16.4.2 关键点解释

model.eval()：切换到推理模式，关闭 Dropout
torch.no_grad()：不计算梯度，节省内存
只取最后位置：logits[:, -1, :]，因为只有最后位置是新预测的
循环生成：每次生成一个 token，加到输入末尾

16.5 Padding 和批量推理

16.5.1 什么是 Padding？

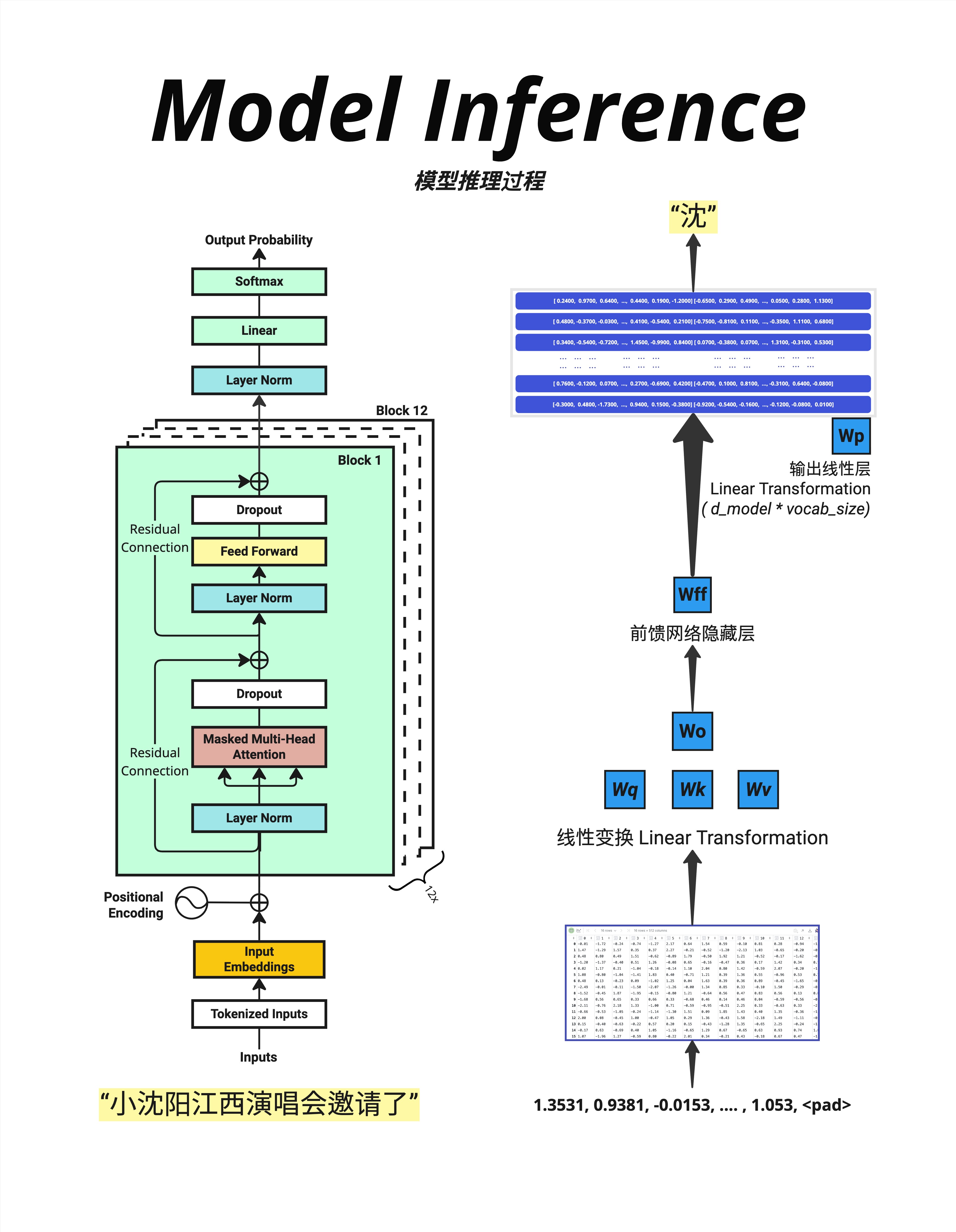
当批量处理不同长度的句子时，需要**填充（Padding）**到相同长度：

句子1："小沈阳江西演唱会邀请了"（15 tokens）
句子2："LLM张老师"（6 tokens）

填充后：
句子1："小沈阳江西演唱会邀请了"
句子2："LLM张老师<pad><pad><pad><pad><pad>"

16.5.2 Padding 的处理

在计算时，需要忽略 padding 位置：

# Attention mask：1 表示真实 token，0 表示 padding
attention_mask = (input_ids != pad_token_id).long()

# 在 Attention 计算中使用 mask
# padding 位置的注意力权重会被设为 0

16.5.3 图中的示例

图中显示：

输入："小沈阳江西演唱会邀请了"
经过模型处理
最后一个真实位置（不是 <pad>）预测下一个词："沈"

16.6 训练与推理的对比

16.6.1 数据流对比

训练时：

完整序列 [seq_len]
    ↓ 一次前向传播
所有位置的预测 [seq_len, vocab]
    ↓ 与目标比较
损失值
    ↓ 反向传播
更新参数

推理时：

Prompt [n]
    ↓ 前向传播
预测位置 n+1
    ↓ 选择 token
新序列 [n+1]
    ↓ 前向传播
预测位置 n+2
    ↓ 选择 token
...（循环直到结束）

16.6.2 计算效率对比

	训练	推理
前向传播次数	1 次 / 序列	N 次 / 序列（N=生成长度）
并行度	高（所有位置并行）	低（必须串行）
瓶颈	内存（存储梯度）	时间（反复前向传播）

这就是为什么推理需要各种优化技术（如 KV Cache，我们将在第 22 章详细讨论）。

16.6.3 Dropout 的行为

	训练	推理
Dropout	激活（随机丢弃）	关闭（不丢弃）
原因	防止过拟合	保持输出稳定

model.train()  # Dropout 激活
model.eval()   # Dropout 关闭

16.7 解码策略

16.7.1 不同的选择方式

推理时，拿到概率分布后，如何选择下一个词？

Greedy Decoding（贪心解码）：

next_token = torch.argmax(probs, dim=-1)  # 选概率最高的

优点：确定性，速度快
缺点：可能生成重复、无聊的文本

Sampling（采样）：

next_token = torch.multinomial(probs, num_samples=1)  # 按概率采样

优点：更有创造性
缺点：可能不连贯

Top-K Sampling：

# 只从概率最高的 K 个词中采样
top_k_probs, top_k_indices = torch.topk(probs, k=50)
next_token = top_k_indices[torch.multinomial(top_k_probs, 1)]

Top-P (Nucleus) Sampling：

# 只从累积概率达到 P 的词中采样
sorted_probs, sorted_indices = torch.sort(probs, descending=True)
cumsum = torch.cumsum(sorted_probs, dim=-1)
mask = cumsum <= 0.9  # P=0.9
# 在 mask 内的词中采样

16.7.2 Temperature 的作用

回顾第 6 章：Temperature 控制概率分布的"锐度"：

probs = F.softmax(logits / temperature, dim=-1)

T < 1：更确定（概率更集中）
T = 1：标准
T > 1：更随机（概率更均匀）

16.8 为什么要自回归？

16.8.1 语言的本质

语言是有序的。"我爱你"和"你爱我"意思完全不同。

自回归生成保证了：

每个词的生成都基于前面的所有词
生成的文本是连贯的
符合语言的自然顺序

16.8.2 其他生成方式

有一些非自回归模型尝试并行生成所有词，但效果通常不如自回归模型好。

原因：

词与词之间有很强的依赖关系
并行生成难以捕捉这种依赖
需要多轮迭代才能收敛

目前最好的语言模型（GPT-4、Claude、LLaMA）都是自回归的。

16.9 本章总结

16.9.1 核心对比

方面	训练	推理
知道答案？	是	否
处理方式	并行	串行
前向传播	1 次/序列	N 次/序列
Dropout	开启	关闭
更新参数	是	否

16.9.2 自回归生成

Prompt → 预测词1 → 加入序列 → 预测词2 → 加入序列 → ...

每一步都依赖前面所有的词，保证生成的连贯性。

16.9.3 核心认知

训练时因为知道所有答案，可以并行处理整个序列；推理时因为答案未知，必须一个词一个词地自回归生成。这种串行生成是推理效率的主要瓶颈，也是为什么需要 KV Cache 等优化技术的原因。

本章交付物

学完这一章，你应该能够：

解释训练和推理的核心区别
理解自回归生成的过程
知道为什么推理比训练慢
了解基本的解码策略（Greedy、Sampling、Top-K）

下一章预告

自回归生成需要反复做前向传播，效率很低。有没有办法加速？这就是 KV Cache 等推理优化技术的用武之地（详见第 22 章）。

但在深入优化之前，我们先来理解训练过程中另一个关键因素——学习率。学习率太大会导致训练震荡，太小又会收敛太慢。下一章，我们来深入理解学习率的作用。