Flash Attention 的核心洞察：GPU 的计算速度远快于内存读写速度，通过巧妙的分块策略和在线算法，我们可以用"多算一点"换取"少读写很多"，最终实现 2-4 倍的端到端加速。

21.1 为什么需要 Flash Attention

21.1.1 一个令人困惑的现象

假设你正在训练一个 Transformer 模型，使用的是顶级的 NVIDIA A100 GPU，理论算力高达 312 TFLOPS（FP16）。按理说，这么强大的计算能力应该能让训练飞快进行。但实际情况是：当序列长度增加时，训练速度急剧下降，而且经常出现 OOM（Out of Memory）错误。

更诡异的是，即使 GPU 显存还有剩余，即使 GPU 利用率看起来很高，Attention 计算仍然成为瓶颈。这是为什么？

答案藏在一个被大多数人忽视的地方：内存带宽。

21.1.2 Attention 的内存困境

让我们回顾一下标准 Attention 的计算公式：

\\text{Attention}(Q, K, V) = \\text{softmax}\\left(\\frac{QK^T}{\\sqrt{d_k}}\\right)V

这个公式看起来很简洁，但隐藏着一个巨大的问题。假设序列长度为 $N$ ，每个 token 的维度为 $d$ ：

$Q$ 的形状是 $[N, d]$
$K$ 的形状是 $[N, d]$
$QK^T$ 的形状是 $[N, N]$

当 $N = 4096$ （这在现代 LLM 中很常见）， $QK^T$ 矩阵的大小是 $4096 \\times 4096 = 16,777,216$ 个元素。如果使用 FP16，这需要约 32MB 的内存。

这还只是单个 Attention 头、单个样本的情况。考虑到：

多头注意力（比如 32 个头）
Batch size（比如 8）
需要存储中间结果用于反向传播

内存需求会爆炸式增长： $32 \\times 8 \\times 32\\text{MB} = 8\\text{GB}$ ，仅仅是存储 Attention 矩阵就需要这么多！

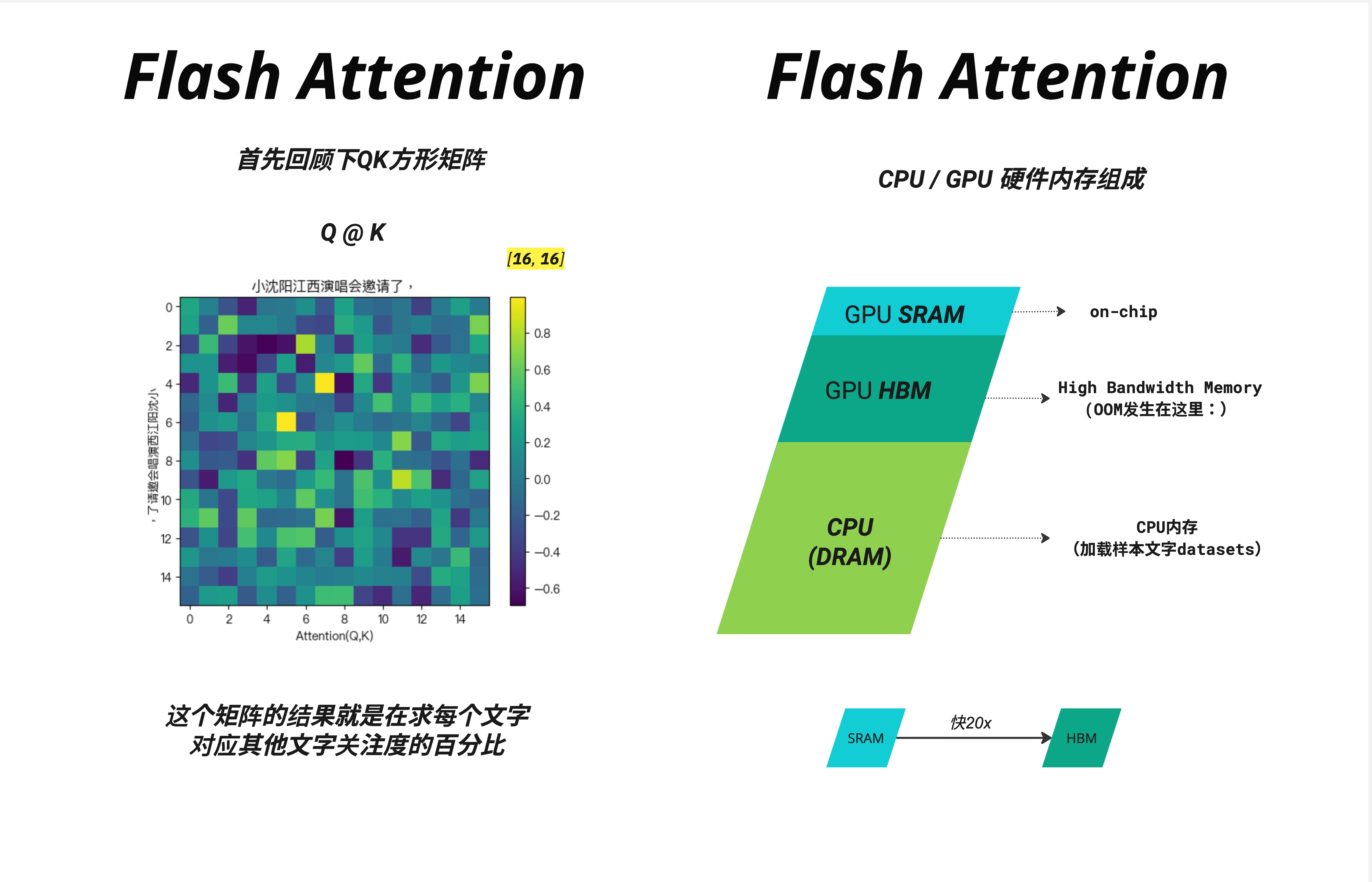
上图左侧展示了 $Q @ K$ 矩阵的可视化——这是一个 $16 \\times 16$ 的小例子，每个格子的值代表了一个 token 对其他 token 的关注程度。而右侧展示了 GPU 的内存层级结构，这是理解 Flash Attention 的关键。

21.1.3 GPU 内存层级：速度与容量的权衡

GPU 的内存并不是一个统一的整体，而是分为多个层级：

层级	名称	容量	速度	说明
片上	SRAM（共享内存/L1/L2缓存）	~20 MB	~19 TB/s	极快但极小
显存	HBM（高带宽内存）	~40-80 GB	~1.5-3 TB/s	GPU 主内存
主机	CPU DRAM	~1 TB	~12.8 GB/s	更大更慢

关键洞察：SRAM 比 HBM 快大约 20 倍！

这就像你的书桌（SRAM）和书架（HBM）的关系：

书桌上放不了几本书，但取用极快
书架能放很多书，但每次去取都要站起来走过去

传统的 Attention 实现是这样工作的：

从 HBM 读取 $Q, K$ → 计算 $QK^T$ → 写回 HBM
从 HBM 读取 $QK^T$ → 做 softmax → 写回 HBM
从 HBM 读取 softmax 结果和 $V$ → 计算最终输出 → 写回 HBM

每一步都涉及大量的 HBM 读写！这就是瓶颈所在。

21.2 传统实现 vs Flash Attention

21.2.1 PyTorch 标准实现的问题

让我们看看 PyTorch 中标准 Attention 的计算过程：

# 标准 Attention 实现
def standard_attention(Q, K, V):
    # 步骤 1: 计算 QK^T，结果存入 HBM
    scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(d_k)

    # 步骤 2: 从 HBM 读取 scores，计算 softmax，结果存回 HBM
    attention_weights = torch.softmax(scores, dim=-1)

    # 步骤 3: 应用 dropout（可选），又是一次 HBM 读写
    attention_weights = dropout(attention_weights)

    # 步骤 4: 从 HBM 读取权重和 V，计算输出
    output = torch.matmul(attention_weights, V)

    return output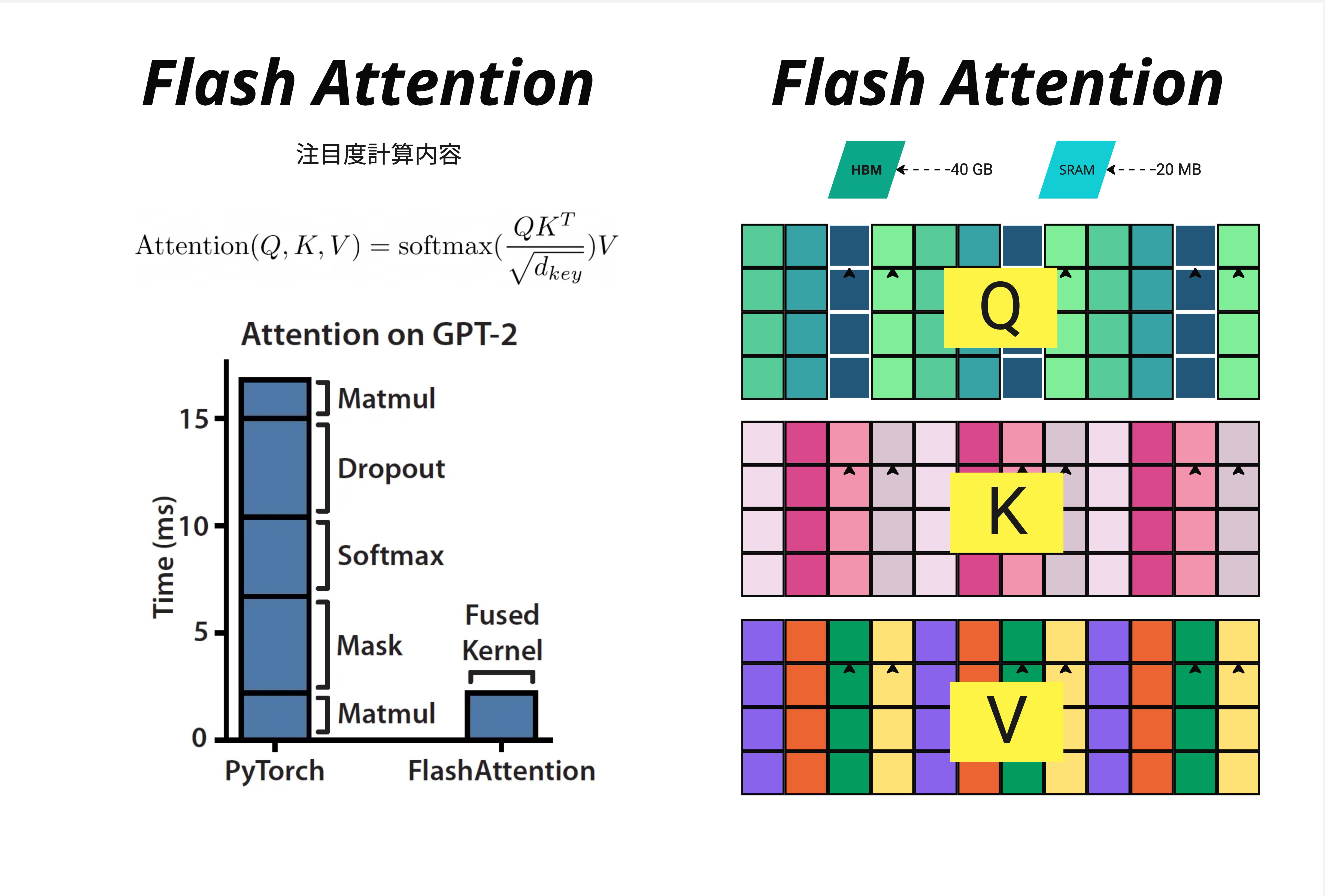

上图左侧的柱状图清楚地展示了问题所在。在 GPT-2 的 Attention 计算中：

PyTorch 实现：需要约 15ms，其中大部分时间花在 Matmul、Dropout、Softmax、Mask 等操作上
Flash Attention：仅需约 3ms，因为它将所有操作融合成一个 Fused Kernel

性能提升了 5 倍！而且这还只是时间上的提升，内存占用的减少更加显著。

21.2.2 内存占用对比

右图展示了 Q、K、V 矩阵在 HBM（~40GB）和 SRAM（~20MB）之间的存储情况。传统方法需要将完整的 $N \\times N$ Attention 矩阵存储在 HBM 中，而 Flash Attention 只需要在 SRAM 中处理小块数据。

内存复杂度对比：

标准 Attention： $O(N^2)$ —— 需要存储完整的 Attention 矩阵
Flash Attention： $O(N)$ —— 只需要存储输入和输出，不需要存储中间的大矩阵

这意味着：

序列长度 2048 时，Flash Attention 节省约 2048 倍的中间内存（ $O(N^2)$ vs $O(N)$ ）
序列长度 4096 时，节省约 4096 倍

注：实际节省倍数约等于序列长度 N，因为从 $O(N^2)$ 降到 $O(N)$ 。

21.3 Flash Attention 的核心思想：Tiling（分块）

21.3.1 分块策略的直觉

Flash Attention 的核心思想可以用一个简单的类比来理解：

想象你要计算一个很大的乘法表（比如 100x100）。传统方法是：

先算出整个乘法表，写在一张大纸上
然后对每一行做处理（softmax）
最后用处理后的结果继续计算

Flash Attention 的方法是：

把大表分成小块（比如 10x10 的小块）
每次只处理一个小块，在小纸条（SRAM）上完成所有计算
边算边更新最终结果，不需要存储整个大表

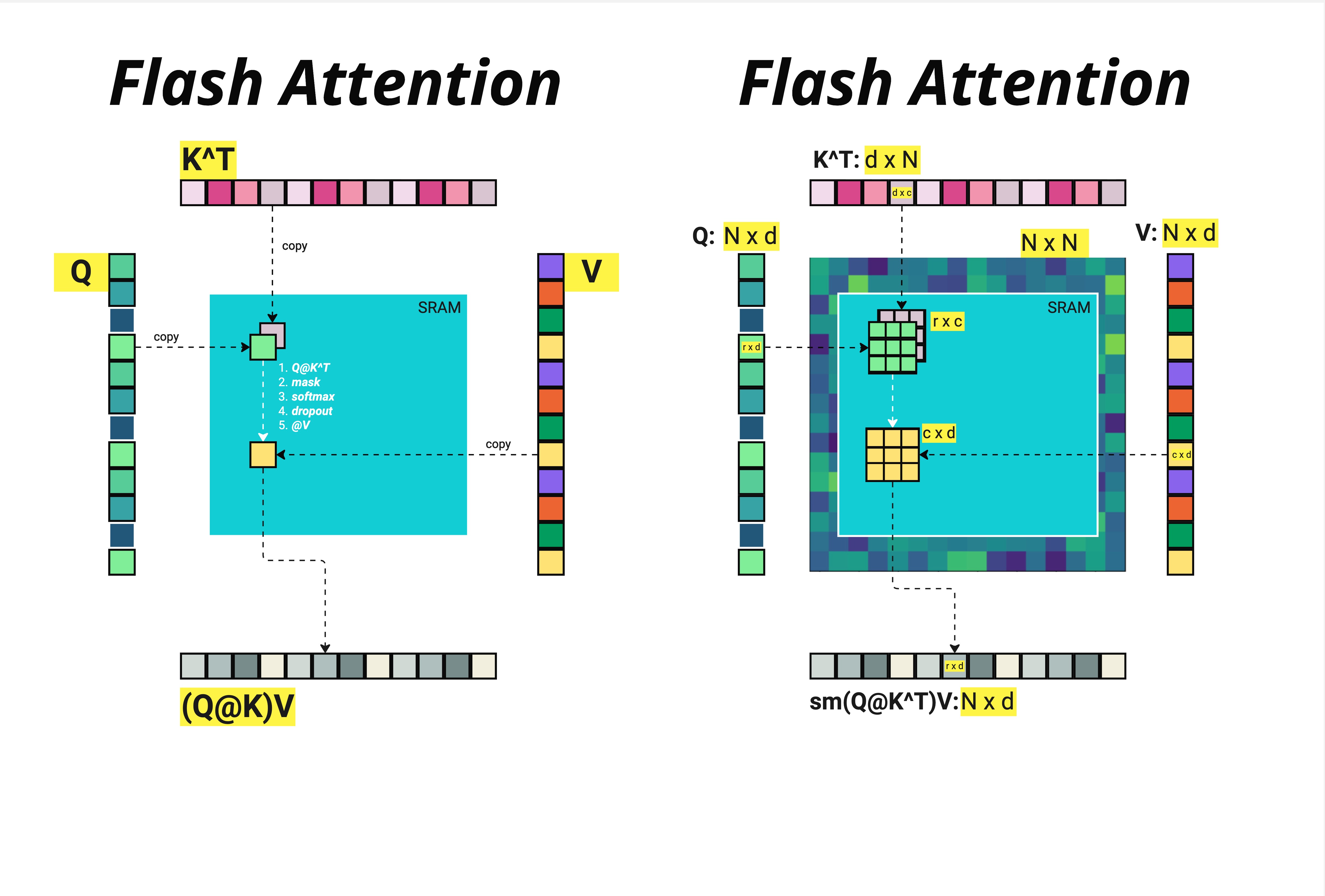
上图清晰地展示了这个过程：

左侧：将 $K^T$ 、 $Q$ 、 $V$ 的小块复制到 SRAM 中
在 SRAM 内完成：1. $Q@K^T$ → 2. mask → 3. softmax → 4. dropout → 5. $@V$
将结果 $(Q@K)V$ 写回 HBM

右侧展示了矩阵维度的对应关系：

$Q$ : $N \\times d$ （例如 4096 x 512）
$K^T$ : $d \\times N$
中间结果 $QK^T$ : $N \\times N$ （这个巨大的矩阵我们不再完整存储！）
输出: $N \\times d$

21.3.2 分块大小的计算

在 NVIDIA A100 GPU 上，SRAM 大小约为 192KB。我们需要在 SRAM 中同时存放：

$Q$ 的一个块： $B_r \\times d$
$K$ 的一个块： $B_c \\times d$
$V$ 的一个块： $B_c \\times d$
输出块： $B_r \\times d$

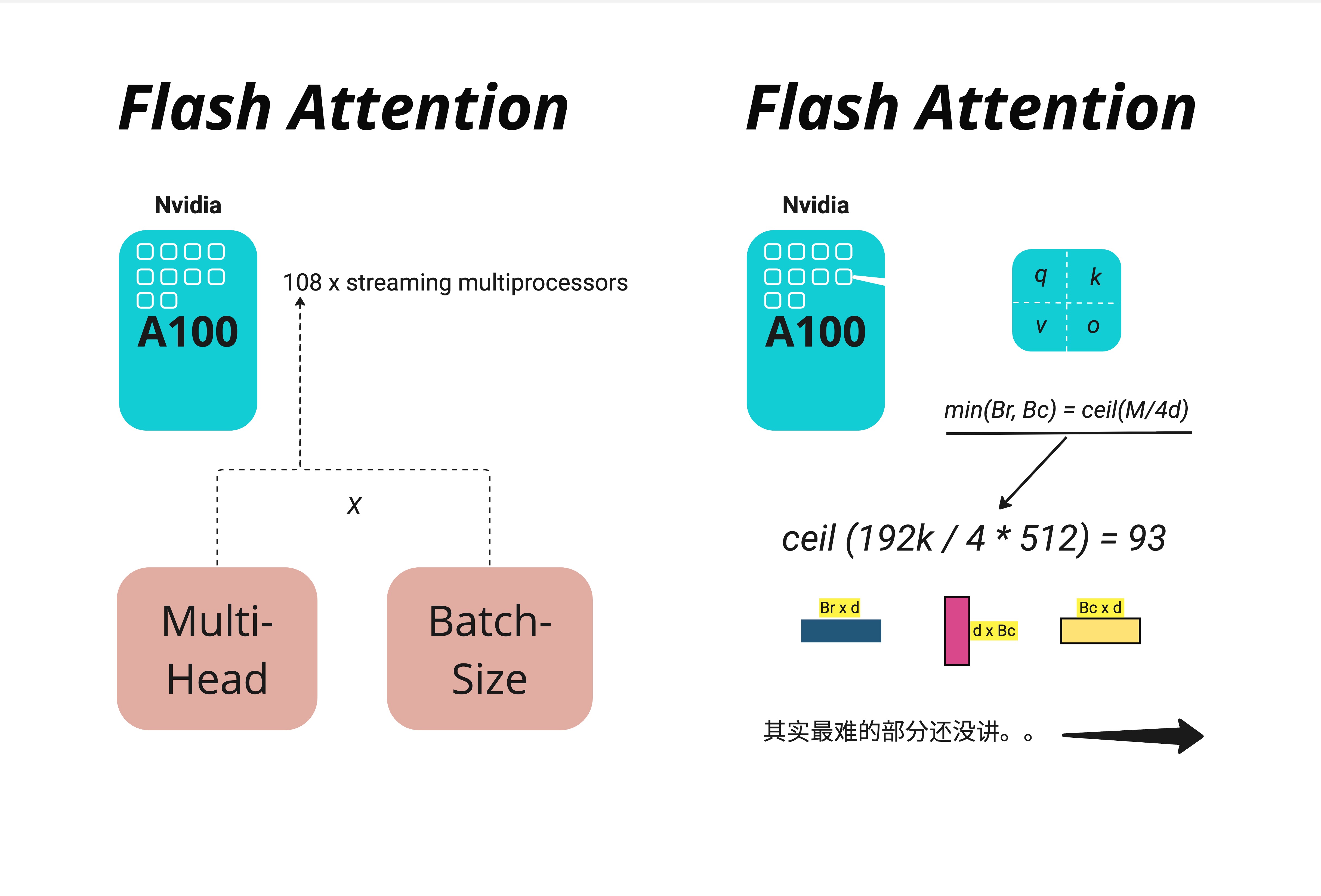
根据上图，A100 有 108 个 Streaming Multiprocessors（SM），每个 SM 都有自己的 SRAM。分块大小的计算公式是：

\\min(B_r, B_c) = \\text{ceil}\\left(\\frac{M}{4d}\\right)

其中 $M$ 是 SRAM 大小（192KB）， $d$ 是 head dimension（通常是 64 或 128）。

例如，当 $M = 192\\text{KB} = 192 \\times 1024$ 字节， $d = 512$ 时：

\\text{ceil}\\left(\\frac{192 \\times 1024}{4 \\times 512}\\right) = \\text{ceil}(96) = 96

但实际实现中，为了对齐和效率，通常会选择 $B_r = B_c = 64$ 或 $128$ 。

21.3.3 分块计算的详细流程

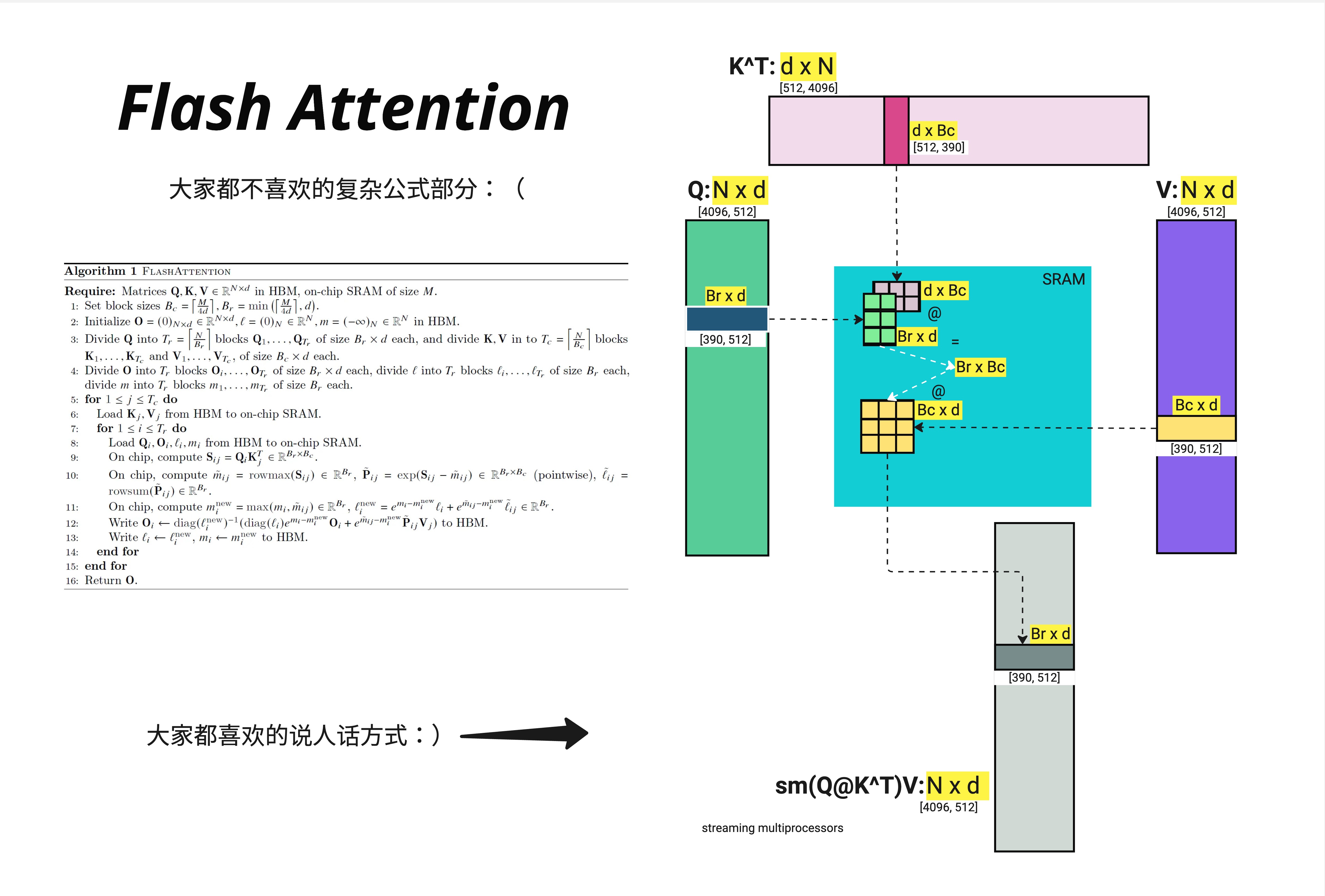
上图展示了 Flash Attention 的完整算法和对应的可视化。让我们用更直观的方式来理解：

输入：

$Q$ : $[4096, 512]$ —— 存储在 HBM 中
$K^T$ : $[512, 4096]$ —— 存储在 HBM 中
$V$ : $[4096, 512]$ —— 存储在 HBM 中

分块：

将 $Q$ 分成 $T_r = \\lceil N/B_r \\rceil$ 个块，每块大小 $[B_r, d]$ ，即 $[390, 512]$
将 $K, V$ 分成 $T_c = \\lceil N/B_c \\rceil$ 个块，每块大小 $[B_c, d]$

核心循环（伪代码）：

for j = 1 to T_c:  # 外层循环：遍历 K, V 的块
    将 K_j, V_j 从 HBM 加载到 SRAM

    for i = 1 to T_r:  # 内层循环：遍历 Q 的块
        将 Q_i 从 HBM 加载到 SRAM

        # 在 SRAM 中完成所有计算
        S_ij = Q_i @ K_j^T          # 小块矩阵乘法
        P_ij = softmax(S_ij)        # 分块 softmax（需要特殊处理！）
        O_i = O_i + P_ij @ V_j      # 累加输出

        将更新后的 O_i 写回 HBM

等等，这里有一个问题：Softmax 是对整行做的，但我们只有一小块数据，怎么办？

这就需要引入 Flash Attention 最巧妙的部分：Online Softmax。

21.4 Online Softmax：分块计算 Softmax 的魔法

21.4.1 标准 Softmax 的问题

先回顾一下 Softmax 公式：

\\text{softmax}(x)_i = \\frac{e^{x_i}}{\\sum_{j=1}^{K} e^{x_j}}

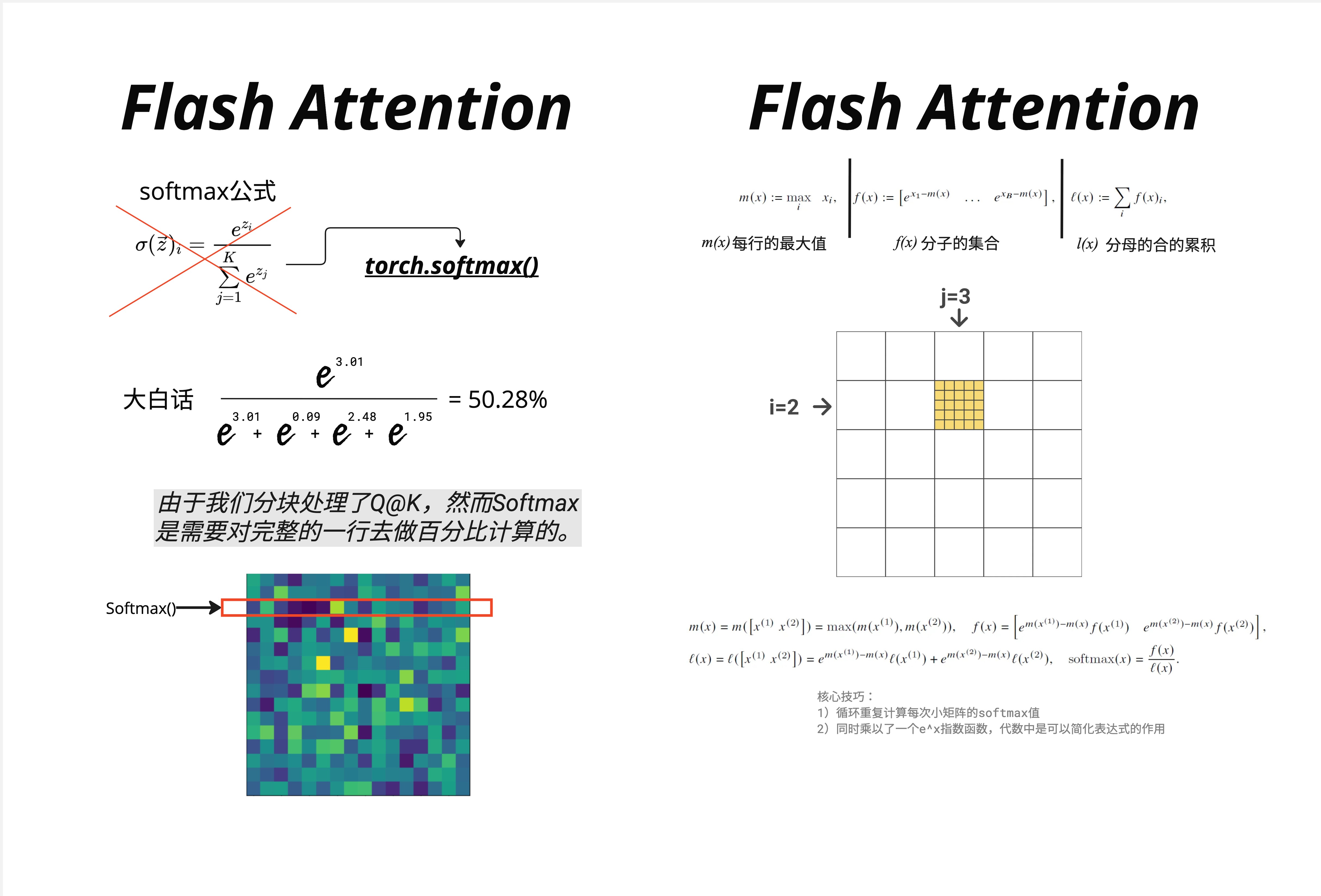
上图左侧展示了标准 Softmax 的计算方式。举个具体例子：

假设一行的值是 $[3.01, 0.09, 2.48, 1.95]$ ，计算第一个元素的 softmax：

\\text{softmax}(3.01) = \\frac{e^{3.01}}{e^{3.01} + e^{0.09} + e^{2.48} + e^{1.95}} = 50.28\\%

问题在于：分母需要所有元素的和。但在分块计算时，我们一次只能看到部分元素！

21.4.2 Online Softmax 的核心技巧

Online Softmax 的关键洞察是：我们可以边看边更新，而不需要一次性看到所有数据。

为了实现这一点，我们需要维护三个量：

$m(x)$ ：当前已见元素的最大值
$f(x)$ ：分子的集合（调整后的指数值）
$l(x)$ ：分母的累积和

当新的数据块到来时，我们可以用以下公式更新：

合并两个块的规则：

假设我们已经处理了第一块 $x^{(1)}$ ，现在来了第二块 $x^{(2)}$ ：

更新最大值： $m(x) = \\max(m(x^{(1)}), m(x^{(2)}))$
更新分子：

$f(x) = \\left[e^{m(x^{(1)}) - m(x)} \\cdot f(x^{(1)}), \\quad e^{m(x^{(2)}) - m(x)} \\cdot f(x^{(2)})\\right]$
更新分母：

$l(x) = e^{m(x^{(1)}) - m(x)} \\cdot l(x^{(1)}) + e^{m(x^{(2)}) - m(x)} \\cdot l(x^{(2)})$
最终 softmax： $\\text{softmax}(x) = \\frac{f(x)}{l(x)}$

21.4.3 为什么需要跟踪最大值？

你可能注意到了，公式中反复出现 $e^{m(x^{(1)}) - m(x)}$ 这样的项。这是为了数值稳定性。

直接计算 $e^{x}$ 当 $x$ 很大时会溢出。标准做法是先减去最大值：

\\text{softmax}(x)_i = \\frac{e^{x_i - \\max(x)}}{\\sum_{j} e^{x_j - \\max(x)}}

在 Online Softmax 中，由于我们分块处理，每个块有自己的局部最大值。当遇到新块时，全局最大值可能会更新，我们需要用 $e^{m_{old} - m_{new}}$ 来"修正"之前的计算结果。

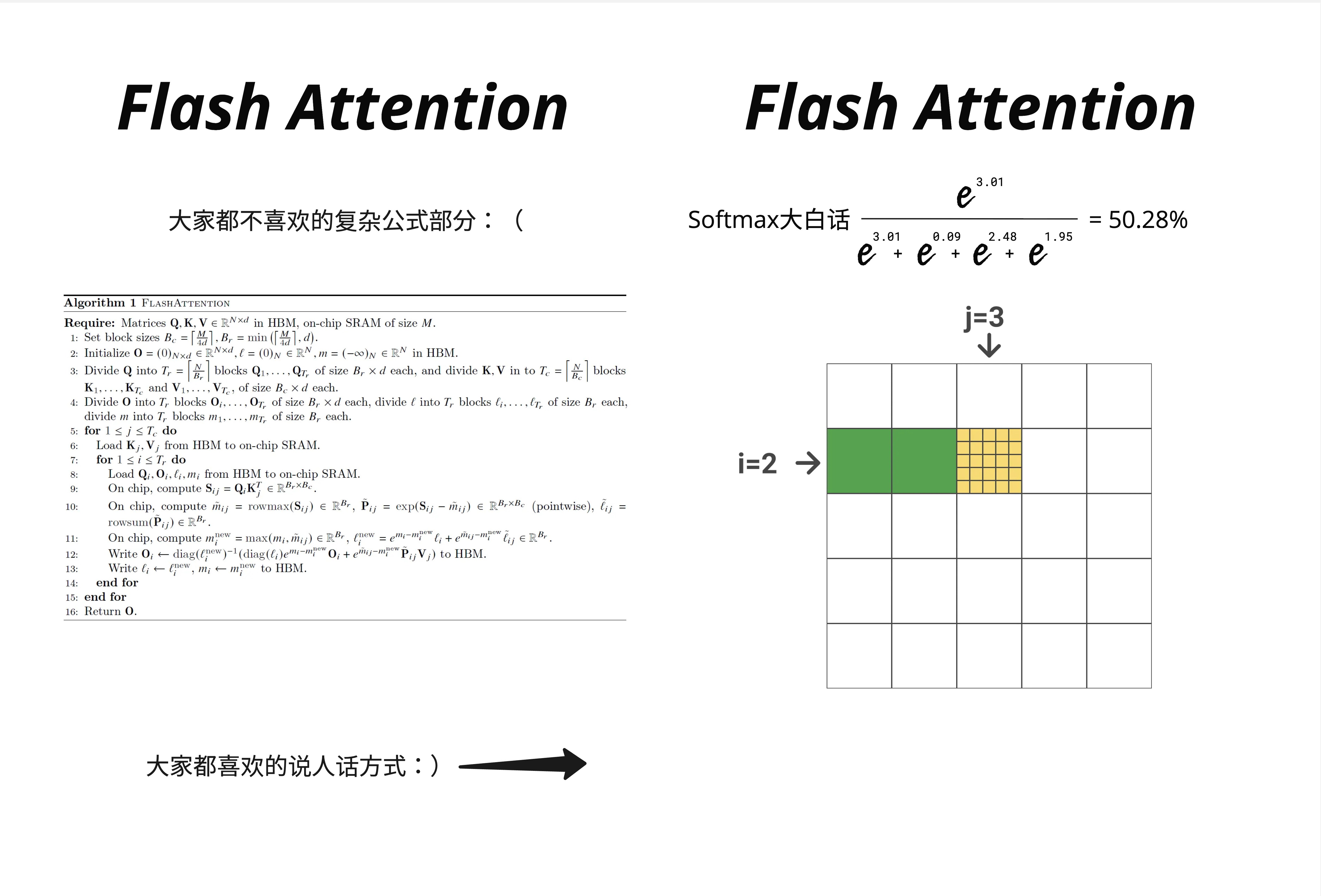
上图右侧展示了分块处理的过程。绿色块表示已经处理完的部分，黄色块表示当前正在处理的块（例如 $i=2, j=3$ 的位置）。

21.4.4 手算示例

让我们用一个小例子来验证 Online Softmax 的正确性。

假设完整的一行是 $[3.01, 0.09, 2.48, 1.95]$ ，我们分成两块处理：

第一块 $x^{(1)} = [3.01, 0.09]$
第二块 $x^{(2)} = [2.48, 1.95]$

处理第一块：

$m^{(1)} = 3.01$
$f^{(1)} = [e^{3.01-3.01}, e^{0.09-3.01}] = [1, 0.053]$
$l^{(1)} = 1 + 0.053 = 1.053$

处理第二块并合并：

$m^{(2)} = 2.48$
$m = \\max(3.01, 2.48) = 3.01$ （最大值没变）
修正因子： $e^{3.01-3.01} = 1$ ， $e^{2.48-3.01} = 0.59$
$f = [1 \\times 1, 1 \\times 0.053, 0.59 \\times e^{0}, 0.59 \\times e^{-0.53}]$
$l = 1 \\times 1.053 + 0.59 \\times (1 + e^{-0.53}) = 1.053 + 0.59 \\times 1.59 = 1.99$

计算第一个元素的 softmax：

\\text{softmax}(3.01) = \\frac{1}{1.99} \\approx 50.25\\%

这与直接计算的 50.28% 非常接近（差异来自我们简化的计算）！

21.5 Flash Attention 完整算法

21.5.1 算法伪代码

现在我们可以理解完整的 Flash Attention 算法了：

Algorithm: FLASHATTENTION

Input: Q, K, V ∈ R^{N×d} in HBM, on-chip SRAM of size M

1. 设置块大小 B_c = ceil(M / 4d), B_r = min(ceil(M / 4d), d)
2. 初始化 O = 0, l = 0, m = -∞ in HBM

3. 将 Q 分成 T_r = ceil(N / B_r) 个块 Q_1, ..., Q_{T_r}
4. 将 K, V 分成 T_c = ceil(N / B_c) 个块 K_1, ..., K_{T_c} 和 V_1, ..., V_{T_c}

5. for j = 1 to T_c do:
6.     从 HBM 加载 K_j, V_j 到 SRAM
7.     for i = 1 to T_r do:
8.         从 HBM 加载 Q_i, O_i, l_i, m_i 到 SRAM
9.         在 SRAM 中计算 S_ij = Q_i @ K_j^T
10.        计算 m̃_ij = rowmax(S_ij), P̃_ij = exp(S_ij - m̃_ij), l̃_ij = rowsum(P̃_ij)
11.        计算 m_i^new = max(m_i, m̃_ij)
12.        计算 l_i^new = e^{m_i - m_i^new} × l_i + e^{m̃_ij - m_i^new} × l̃_ij
13.        更新 O_i ← diag(l_i^new)^{-1} × (diag(l_i) × e^{m_i - m_i^new} × O_i + e^{m̃_ij - m_i^new} × P̃_ij × V_j)
14.        将 O_i, l_i^new, m_i^new 写回 HBM
15.    end for
16. end for
17. Return O

21.5.2 IO 复杂度分析

Flash Attention 的巧妙之处在于大大减少了 HBM 访问次数。

标准 Attention 的 IO 复杂度：

读取 $Q, K$ ： $O(Nd)$
写入 $S = QK^T$ ： $O(N^2)$
读取 $S$ 做 softmax： $O(N^2)$
写入 softmax 结果： $O(N^2)$
读取 softmax 结果和 $V$ ： $O(N^2 + Nd)$
写入输出： $O(Nd)$
总计： $O(Nd + N^2)$

Flash Attention 的 IO 复杂度：

外层循环读取 $K_j, V_j$ ： $T_c$ 次，每次 $O(B_c d)$
内层循环读写 $Q_i, O_i$ ： $T_r \\times T_c$ 次，每次 $O(B_r d)$
总计： $O\\left(\\frac{N^2 d^2}{M}\\right)$

当 SRAM 大小 $M$ 足够大时（通常 $M \\gg d$ ），Flash Attention 的 IO 复杂度接近 $O(N^2 d / M)$ ，比标准实现的 $O(N^2)$ 好很多！

21.6 Flash Attention 1 vs Flash Attention 2

21.6.1 FA1 的局限性

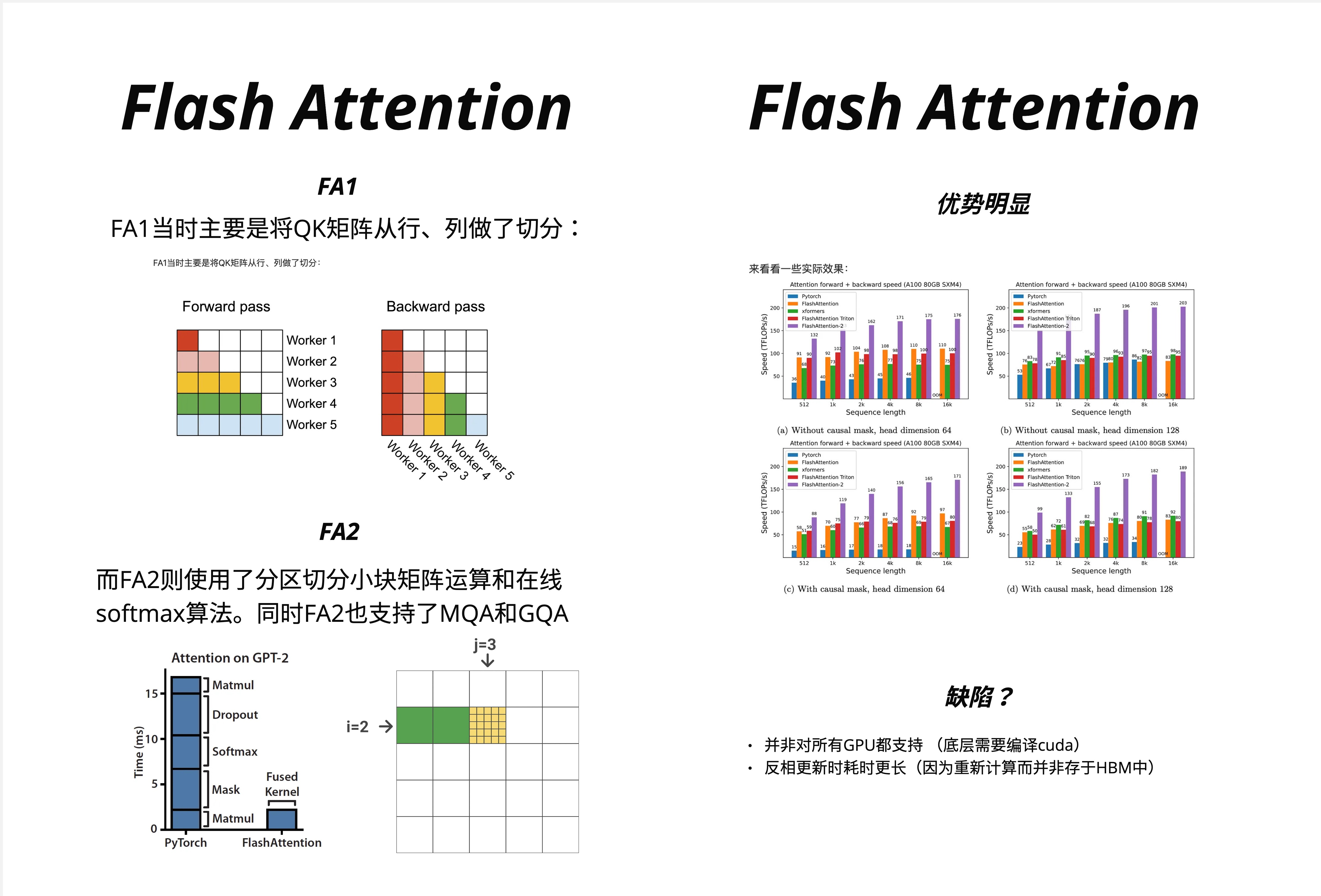
Flash Attention 1（2022 年发布）虽然已经实现了巨大的性能提升，但还有优化空间。

上图左侧展示了 FA1 的工作方式：

按行、列切分 QK 矩阵
Forward pass 和 Backward pass 分别由多个 Worker 并行处理
但 Worker 之间需要同步，造成了一些等待时间

21.6.2 FA2 的改进

Flash Attention 2（2023 年发布）做了几个关键改进：

更好的并行策略：
- FA2 使用了分区切分小块矩阵运算
- 减少了 Worker 之间的同步开销
- 更充分地利用 GPU 的 Streaming Multiprocessors
支持 MQA 和 GQA：
- Multi-Query Attention（MQA）
- Grouped-Query Attention（GQA）
- 这些变体在推理时特别有用，FA2 原生支持
更高效的 Online Softmax 实现：
- 优化了数值计算的精度和效率
- 减少了寄存器使用

上图右侧展示了性能对比：

在 A100 80GB SXM4 GPU 上测试
不同序列长度（512 到 16k）和 head dimension（64 和 128）
FlashAttention-2 consistently 达到最高吞吐量，通常比 FA1 快 1.5-2 倍

21.6.3 性能数据

根据官方 benchmark：

配置	PyTorch	FA1	FA2
Seq 2k, head_dim 64	~50 TFLOPS	~120 TFLOPS	~175 TFLOPS
Seq 4k, head_dim 64	~45 TFLOPS	~110 TFLOPS	~170 TFLOPS
Seq 8k, head_dim 128	~40 TFLOPS	~100 TFLOPS	~165 TFLOPS

FA2 能够达到 A100 理论峰值（312 TFLOPS）的约 50-70%，这对于一个 memory-bound 的操作来说已经非常优秀了。

21.7 Flash Attention 的局限性

尽管 Flash Attention 非常强大，但也有一些局限性需要了解：

21.7.1 硬件兼容性

需要特定 GPU 架构：Flash Attention 底层使用 CUDA 实现，需要较新的 NVIDIA GPU（Ampere 架构及以上效果最好）
需要编译 CUDA 代码：安装过程可能遇到编译问题
不支持所有 GPU：老旧的 GPU 或非 NVIDIA GPU 无法使用

21.7.2 反向传播的开销

由于 Flash Attention 不存储完整的 Attention 矩阵，在反向传播时需要重新计算这些值。这意味着：

反向传播耗时更长：相比标准实现，反向传播需要额外的计算
总体仍然更快：因为节省的内存带宽远超额外的计算开销

21.7.3 特定功能支持

某些 Attention 变体可能需要特殊处理：

Sliding Window Attention
Sparse Attention patterns
自定义的 Attention mask

好消息是，Flash Attention 2 已经支持了大部分常见的变体。

21.8 实际使用：代码示例

21.8.1 安装 Flash Attention

# 推荐使用 pip 安装
pip install flash-attn --no-build-isolation

# 或者从源码安装（需要 CUDA toolkit）
git clone https://github.com/Dao-AILab/flash-attention.git
cd flash-attention
pip install .

21.8.2 基本使用

import torch
from flash_attn import flash_attn_func

# 准备输入
batch_size = 2
seq_len = 4096
num_heads = 32
head_dim = 128

# Q, K, V 形状: [batch, seq_len, num_heads, head_dim]
q = torch.randn(batch_size, seq_len, num_heads, head_dim,
                dtype=torch.float16, device='cuda')
k = torch.randn(batch_size, seq_len, num_heads, head_dim,
                dtype=torch.float16, device='cuda')
v = torch.randn(batch_size, seq_len, num_heads, head_dim,
                dtype=torch.float16, device='cuda')

# 调用 Flash Attention
output = flash_attn_func(q, k, v, causal=True)  # causal=True 用于自回归模型

21.8.3 与 PyTorch 集成

PyTorch 2.0+ 已经内置了 Flash Attention 支持：

import torch
import torch.nn.functional as F

# 使用 scaled_dot_product_attention（会自动选择最佳实现）
output = F.scaled_dot_product_attention(
    query, key, value,
    attn_mask=None,
    dropout_p=0.0,
    is_causal=True,
    scale=None
)

# PyTorch 会自动判断是否使用 Flash Attention、Memory Efficient Attention 或标准实现

21.8.4 在 Hugging Face Transformers 中使用

from transformers import AutoModelForCausalLM

# 加载模型时启用 Flash Attention 2
model = AutoModelForCausalLM.from_pretrained(
    "meta-llama/Llama-2-7b-hf",
    torch_dtype=torch.float16,
    attn_implementation="flash_attention_2"  # 关键参数
)

21.9 本章要点回顾

GPU 内存瓶颈：现代 GPU 的计算速度远快于内存带宽，Attention 计算的瓶颈在于 HBM 读写，而非算力
内存层级：
- SRAM：~20MB，极快（~19 TB/s）
- HBM：~40GB，相对慢（~1.5 TB/s）
- SRAM 比 HBM 快约 20 倍
Tiling 分块策略：
- 将大矩阵分成小块，在 SRAM 中完成所有计算
- 避免将 $N \\times N$ 的 Attention 矩阵写入 HBM
- 内存复杂度从 $O(N^2)$ 降到 $O(N)$
Online Softmax：
- 维护 $m(x)$ （最大值）、 $f(x)$ （分子）、 $l(x)$ （分母）
- 边处理边更新，不需要看到完整的一行
- 保证数值稳定性
FA1 vs FA2：
- FA2 有更好的并行策略
- FA2 支持 MQA/GQA
- FA2 比 FA1 快 1.5-2 倍
实际效果：
- 端到端训练速度提升 2-4 倍
- 内存占用大幅降低
- 支持更长的序列长度

21.10 延伸阅读

Flash Attention 论文：
- FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness（2022）
- FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning（2023）
官方实现：
- GitHub: Dao-AILab/flash-attention
相关技术：
- Memory Efficient Attention（xFormers）
- PagedAttention（vLLM）
- Flash Decoding

21.11 下一章预告

在下一章《KV Cache：推理加速的关键》中，我们将探讨另一个重要的优化技术。KV Cache 解决的是推理阶段的重复计算问题：在自回归生成时，每生成一个新 token 都需要对之前所有 token 做 Attention，如果不缓存 K、V 矩阵，计算量会随着序列增长而急剧增加。

KV Cache 和 Flash Attention 是互补的技术：

Flash Attention：优化单次 Attention 计算的内存效率
KV Cache：避免推理时的重复计算

两者结合使用（如 Flash Decoding），可以实现更快的推理速度。